2018年5月28日

我最喜歡的幾個空間：阿涅西的女巫

這條不起眼、被誤譯的曲線到底意味著什麼？

本文發表於《大眾科學》的前部落格網路，反映作者的觀點，不一定代表《大眾科學》的觀點

瑪麗亞·蓋塔納·阿涅西出生於1718年5月16日，所以她的三百週年紀念日是在本月早些時候。我為史密森尼雜誌寫了一篇文章來紀念這個日子。如果現代數學愛好者瞭解阿涅西，最有可能的是透過女巫曲線。這條曲線的名字來源於一個誤譯，由於阿涅西虔誠的宗教信仰，這個誤譯更顯得諷刺。阿涅西在逐漸離開數學領域、投身於虔誠的慈善事業之前，寫了一本開創性的微積分教科書鉅著，卻永遠揹負著女巫的名字，這可能會讓人感到不滿，但我們或許應該感謝這個誤譯，因為它讓那些學過微積分的人如此瞭解她。

阿涅西的女巫是斯蒂格勒命名法則的一個絕佳例子，該法則指出，以人名命名的科學發現都不是以發現它的人的名字命名的。畢達哥拉斯並不是第一個知道畢達哥拉斯定理的人，帕斯卡三角形在帕斯卡活著之前幾個世紀就為中國數學家所知，而阿涅西的女巫也不是由阿涅西發現的。皮埃爾·德·費馬（1607-1665）研究過一般形式為（a²-x²）y=a³的曲線，而圭多·格蘭迪在1703年的一篇論文中包含了這條曲線。

格蘭迪最初給這條曲線命名為versiera，說他從拉丁語單詞versoria改編而來，而versoria又來源於表示“轉動”的詞。事實上，在某些方面，2018年不僅是阿涅西的300週年誕辰，也是女巫曲線的300週年誕辰；格蘭迪在1703年討論過這條曲線，但他直到1718年才將其命名為versiera。

關於支援科學新聞

如果您喜歡這篇文章，請考慮透過以下方式支援我們屢獲殊榮的新聞報道訂閱。透過購買訂閱，您將幫助確保有關當今塑造我們世界的發現和想法的具有影響力的故事的未來。

約翰·科爾森，這位將阿涅西的鉅著翻譯成英文的英國牧師和數學家，將 versiera 翻譯為 avversiera，意思是女魔頭或女巫。想聽聽一位脾氣暴躁的數學史學家對這個誤譯的看法嗎？（或者至少是一位數學史學家的脾氣暴躁的看法？）看看 C. Truesdell 的這篇文章。“如果有人想了解我在浪費時間尋找和收集上述資料後的感受，他不妨聽聽K. P. E. 巴赫的 D 小調羽管鍵琴協奏曲。”

女巫曲線是什麼？當你深入瞭解時，它實際上是一條不起眼的曲線，在她書中是一個有用的例子，只是許多例子中的一個。我們將看看女巫曲線在阿涅西的著作《分析機構》中的首次出現，由約翰·科爾森翻譯

給定直徑為 AC 的半圓 ADC；需要從它找到一個點 M，使得畫出垂直於直徑 AC 的直線 MB，該直線與圓相交於 D，則 AB.BD::AC.BM。而且，因為有無數個點可以滿足這個問題，所以需要這些點的軌跡。

這個設定很需要一個圖表，阿涅西提供了一個，如圖表頂部所示。（據說她把一臺印刷機搬進了自己的房子，以便親自監督《分析機構》的印刷，並確保她繪製的許多圖表都能正確地複製。）在這張圖中更容易看清楚。

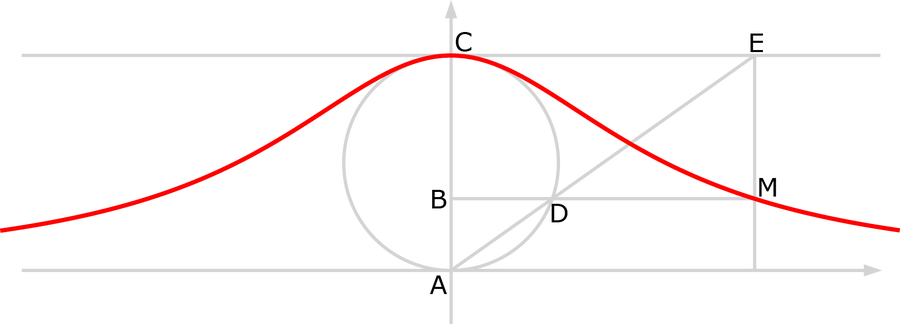
女巫曲線是紅色的。圖片來源：基於 zorgit *Wikimedia*(CC BY-SA 3.0)

透過一些基本的幾何知識，阿涅西推匯出了這條曲線的方程。在她的變數中，她得出方程 y=a(√(a-x)/(√x)。（對於今天的我們來說，她的變數是顛倒的。她用x表示垂直距離，用y表示水平距離。我們會做相反的事情。）在後面的一個問題中，她展示了一種描述這條曲線的等效方法，這導致了以下 GIF，說明了這條曲線一半的軌跡。

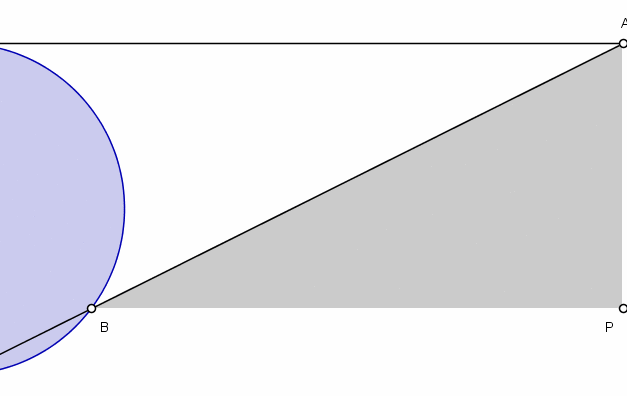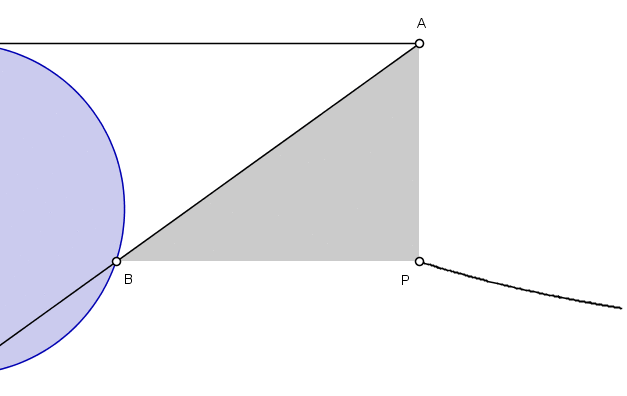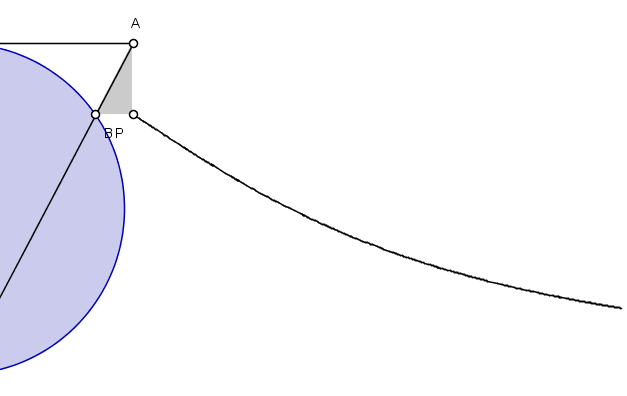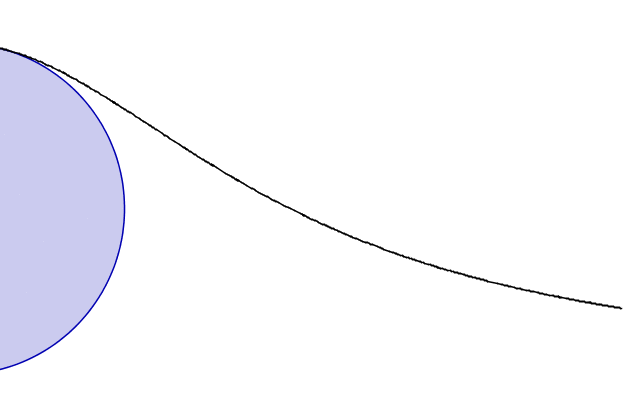
一個顯示阿涅西的女巫曲線的圖表。圖片來源：Merrill *Wikimedia*

後來她還找到了這條曲線的拐點。（這條曲線中間部分像帽子一樣向下彎曲，兩端像碗一樣向上彎曲。帽子和碗之間過渡的點是拐點。）

關於女巫曲線，沒有太多其他要說的了。它是一條不錯的曲線，但沒什麼特別之處。許多微積分學生都用它來探索引數方程，它與一種被稱為柯西分佈的病態機率分佈有關。如果科爾森在翻譯的時候沒有發揮一點想象力，我們可能沒有太多理由在阿涅西書中數十個例子中特別記住它。這表明良好的品牌塑造對於一條渴望聚光燈的勇敢曲線來說是多麼重要。

想更多地瞭解女巫曲線嗎？感謝網際網路的魔力，您可以免費閱讀阿涅西書籍中的關於女巫曲線的內容，無論是義大利語（第 1 卷，第 2 卷）還是科爾森的英語翻譯。La versiera 出現在義大利語版本的第 382 頁、392 頁和 561 頁。該圖表是第一卷後面的圖 135。女巫曲線出現在英文版第 1 卷的第 222 頁和 229 頁以及第 2 卷的第 79 頁。您還可以在線上圖形計算器 Desmos 上探索這條曲線。