2016年4月18日

我最喜歡的一些空間：沃利斯篩

這個奇怪的分形物體讓你從正方形中“擠出 π”

本文發表於《大眾科學》的前部落格網路，反映了作者的觀點，不一定反映《大眾科學》的觀點

幾周前我從沒聽說過沃利斯篩，但它很快在我的最喜愛空間列表中佔據了一席之地。我從 Matt Parker 的這個影片中瞭解到了這個空間。

Parker 從未指名沃利斯篩，但它就在那裡。沃利斯篩是一個分形物體，最容易透過從謝爾賓斯基地毯開始解釋。謝爾賓斯基地毯是一個二維分形，有點類似於我去年寫過的康託集。要製作一個，取一個邊長為 1 的正方形，將其分成 9 個小正方形，然後移除中間的正方形。然後將每個剩餘的正方形分成 9 個小正方形，並移除中間的正方形，依此類推。

關於支援科學新聞

如果您喜歡這篇文章，請考慮透過以下方式支援我們屢獲殊榮的新聞報道訂閱。透過購買訂閱，您將幫助確保未來能夠繼續講述關於塑造我們當今世界的發現和思想的具有影響力的故事。

謝爾賓斯基地毯構造的六個階段。圖片：KarocksOrkav, via Wikimedia Commons。CC BY-SA 3.0。

沃利斯篩的起始方式與謝爾賓斯基地毯相同：取一個邊長為 1 的正方形，並移除中間的九分之一。然後事情變得有趣起來。我們沒有移除所有剩餘正方形的中間九分之一，而是將每個正方形分成 5×5 的網格而不是 3×3，並移除每個正方形的中間正方形，最終得到總面積的 1/25。在下一步中，我們將所有剩餘的正方形分成 7×7 的網格，並從每個正方形中移除中間正方形，即剩餘面積的 1/49。

與謝爾賓斯基地毯不同，我們總是移除 1/9，而沃利斯篩每次移除剩餘集合的比例較小。謝爾賓斯基地毯最終的面積為零，就像康託集一樣，但沃利斯篩具有正面積，就像一個被稍微“增肥”的肥康託集。

不過，在開始進行一些計算之前，我應該指出，關於沃利斯篩到底是什麼，存在一些歧義。我描述的圖形面積為 π/4，與半徑為 1 的四分之一圓的面積相同。有些人覺得將四個這樣的圖形拼在一起得到面積為 π，或一個完整的單位圓，並稱該圖形為沃利斯篩更令人滿意。在這篇文章中，我將堅持我之前的定義。

無論如何，沃利斯篩的面積與圓的面積密切相關。為什麼？這一切都歸結於沃利斯乘積。英國數學家約翰·沃利斯在 1655 年推匯出了這個奇特的公式

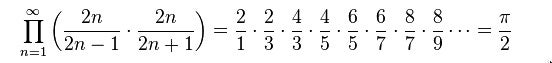
乍一看，這個乘積似乎與沃利斯篩沒有太大關係，但讓我們重寫一下。我們將忽略開頭的 2/1，並將剩餘的項配對。我們得到 2/3×4/3=8/9，4/5×6/5=24/25，依此類推。當我們以這種方式看待乘積時，沃利斯篩就顯現出來了。

在建立篩子的第一步中，當我們移除正方形的中間九分之一時，我們剩下的面積為 8/9。然後，當我們移除剩餘正方形的中間二十五分之一時，我們剩下剩餘面積的 24/25，總面積為 8/9×24/25。然後我們移除每個剩餘正方形的中間 1/49，剩下剩餘面積的 48/49，即原始正方形的 8/9×24/25×48/49。總共（並考慮到我們之前忽略的 2），我們發現沃利斯篩的面積為 π/4，與半徑與篩子邊長相同的四分之一圓的面積相同。

我想知道是否有一種簡單的方法可以看出沃利斯篩與圓如此密切相關。也就是說，如果你擠出所有的空白空間，你會得到一個四分之一圓嗎？我設想將所有東西都推向左下角。

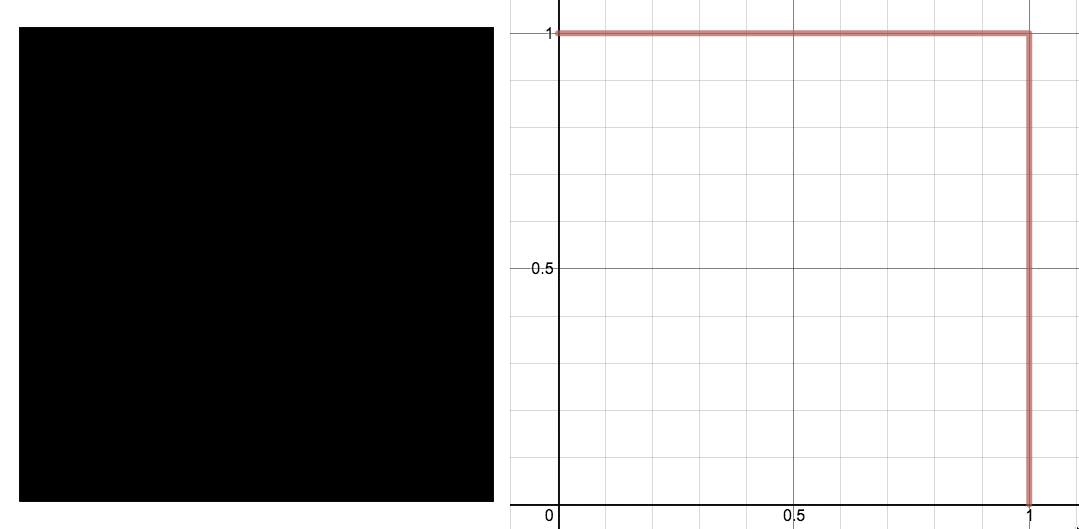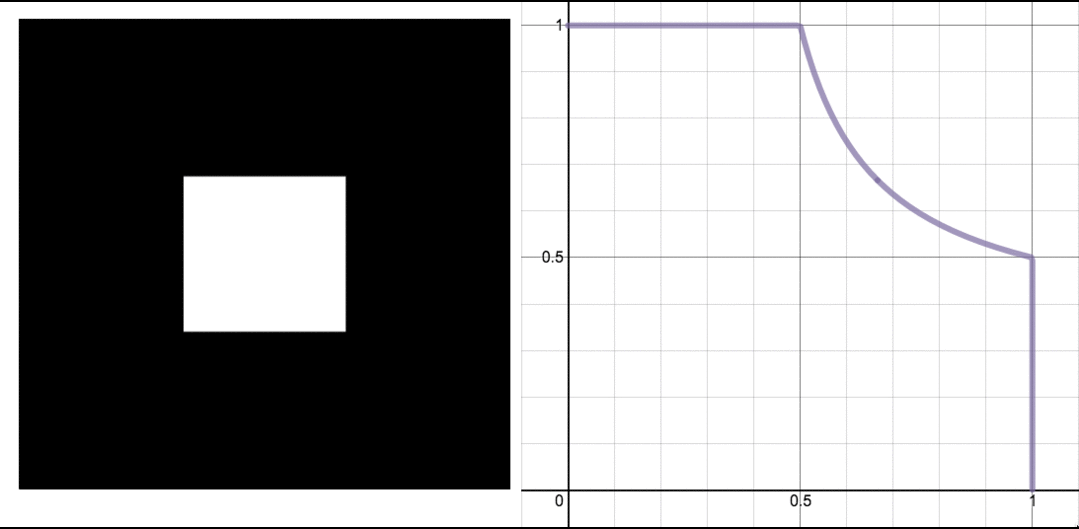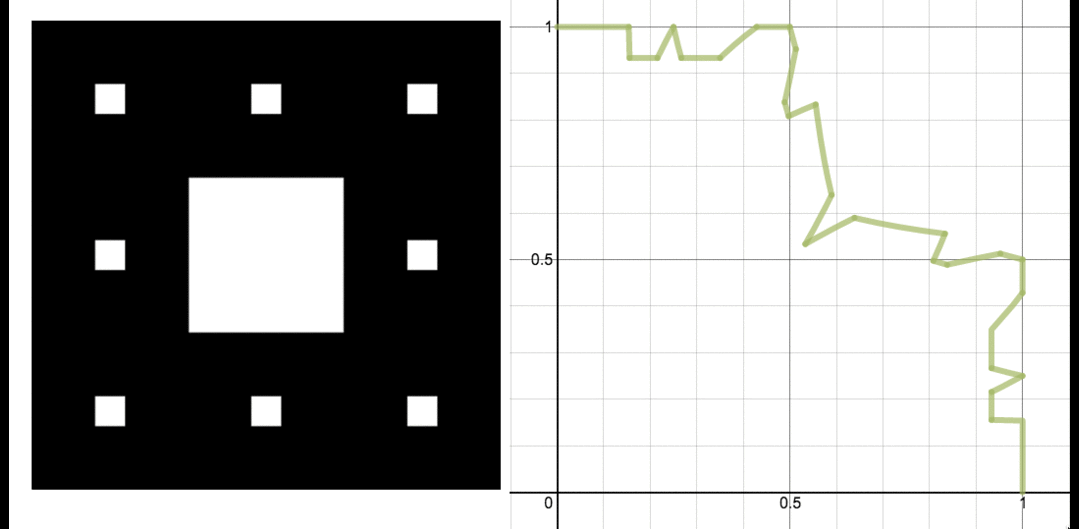
一個動畫，展示了沃利斯篩的三個階段，以及如果我們把所有東西都擠到正方形的左下角會發生什麼的視覺化效果。圖片：Evelyn Lamb，在 Desmos 的協助下製作。

可惜的是，我對簡單解釋的希望立刻破滅了：第一步，移除中間的九分之一，在某些地方移除了足夠的長度，以至於最終不可能得到圓形的東西。

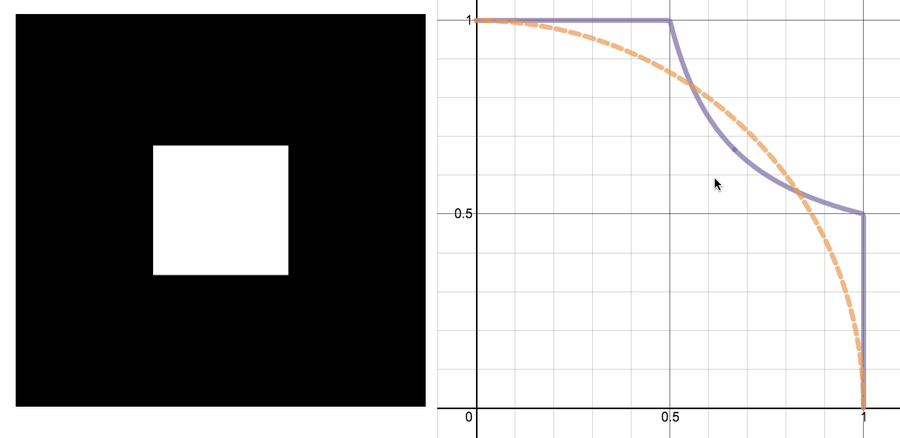
左圖：移除了中間九分之一的正方形。右圖：圖表顯示了將正方形向下和向左擠壓的結果（實線紫色曲線）與圓形楔形（虛線橙色曲線）的對比。圖片：Evelyn Lamb。

關於這個有趣的小形狀，我剩下的問題多於答案。有沒有一種簡單的方法可以看出它的面積應該與四分之一圓的面積相同？如果我把它完全壓扁，它會是什麼樣子？邊界會是有限長度嗎，還是最終我會得到更像科赫曲線的東西？我們甚至還沒有討論到三維版本！正如 Parker 在帖子頂部的影片中指出的那樣，在三維空間中類似的構造會得到一個體積與單位球體相同的物體！我們可以在更高的維度中做同樣的事情嗎？

我希望沃利斯篩和相關問題像 nerd snipe 你一樣 nerd snipe 我。如果您渴望瞭解更多資訊，Ed Pegg 的文章“從門格海綿中擠出 pi”和 Mike Lawler 關於與孩子們分享沃利斯篩的博文是您自己探索的良好起點。