本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
啊,不起眼的圓環:初學拓撲學家的朋友,也是理論與實踐之間差距的體現。圓環有許多生命,並在數學的各個領域中出現。
首先,它具有拓撲生命。拓撲學並不關心你的確切形狀,它只關心大規模的特徵。具體來說,它關心的是物體在拉伸或擠壓時保持不變的方面,只要沒有撕裂。在拓撲世界中,圓環是一個二維空間,或曲面,帶有一個孔。(更專業一點說,它是一個可定向的虧格為一的曲面。)拓撲學家渴望將自己與更具吸引力的糕點主題聯絡起來,將圓環描述為甜甜圈,儘管要令人討厭地精確地說,它只是糖霜。(甜甜圈的麵包是一個三維空間,稱為實心圓環。)
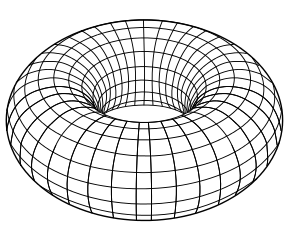
圖片來源:公共領域,來自維基共享資源。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道: 訂閱。透過購買訂閱,您正在幫助確保未來能夠繼續講述關於發現和塑造我們當今世界的思想的具有影響力的故事。
通常,我們將圓環表示為一個豐滿的甜甜圈,但拓撲學家也偏愛一種更抽象的方式來描繪它。在這張圖中,我們將其繪製為一個帶有少量標記(稱為標識)的矩形。
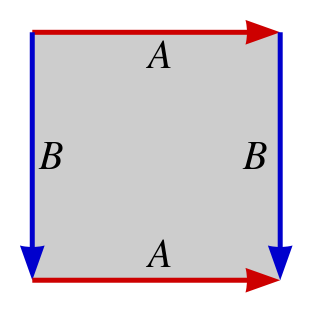
頂部標記為“A”的箭頭與底部標記為“A”的箭頭粘合在一起,左側標記為“B”的箭頭與右側標記為“B”的箭頭粘合在一起。圖片來源:公共領域,來自維基共享資源。
就像經典的電腦遊戲《小行星》一樣,當您從矩形的頂部向上移動時,您會在底部重新出現,而穿過右側會導致您在左側重新出現。雖然這張圖不如甜甜圈那麼誘人,但它仍然向我們展示了圓環的所有重要拓撲性質。
平坦矩形的圖片也很好地過渡到圓環的另一個生命,即它作為幾何物體的生命。與拓撲學相反,幾何學確實關心確切的形狀和距離。豐滿的圓環和纖細的圓環在拓撲學上是相同的,但在幾何學上是不同的。
幾何學家關心圓環的矩形圖片,因為它是一個有限的曲面,從根本上來說是平坦的,就像無限平面一樣。如果您曾經意識到格陵蘭島的面積是非洲的7%,而不是幾乎相同的大小,那麼您就暗中意識到球體無法以保留距離的方式展平到平面上。那是因為它是正彎曲的,而平面是平坦的。還有負彎曲的曲面,它們也不能在沒有一些變形的情況下展平到平面上。
圓環的矩形圖片證明了圓環是平坦的。那麼,如果能夠將圓環視為三維空間中的平坦曲面,而不是僅僅在紙上繪製並使用我們的想象力,那將是非常好的。我們可以嘗試透過在矩形圖片中執行標識來實現這一點。我們從一個矩形開始。
.JPG?w=300)
第一個粘合過程將我們從平坦的紙片變成圓柱體。
.JPG?w=300)
第二個粘合過程將圓柱體的兩端連線在一起。
.JPG?w=300)
問題就在這裡。組裝這個圓環的過程並不像計劃的那麼順利。這是一個理論與實踐的皺巴巴的碰撞。
.JPG?w=300)
#sadtorusselfie(#悲傷圓環自拍)
當任何數學物件進入現實世界時,都不是完美的。我們畫的任何圓都不是完全理想的,而且我們畫它的表面也不是真正的二維物體。但是透過一些小心和一個好的圓規,我們可以製作一個足夠接近我們目的的圓。另一方面,圓環有點像一場噩夢。
那麼,我們能否希望將圓環放置在三維空間中,使其距離不會失真呢?

基於公共領域影像,來自維基共享資源。
我們能做到!但這並不像你可能希望的那麼簡單。
一種選擇是放棄曲面的光滑性。在平面中,矩形沒有任何褶皺,但如果我們加入一些褶皺,我們就可以讓事情奏效。有很多方法可以實現這一點。幾年前我做了一個。
.jpg?w=300)
數學 3D 列印奇才 亨利·塞格曼 有一個很好的例子,其中脊是鉸接的。
如果我想要更多呢?如果我想消除那些刺耳的、難看的褶皺呢?好吧,我們也可以做到!但這變得有點複雜。在 2012 年,文森特·博雷利、賽義德·賈布拉內、弗朗西斯·拉扎勒斯、鮑里斯·蒂貝爾和達米安·羅默發表了第一批在三維空間中實現平坦圓環而沒有任何鋸齒狀拐角的圖片。他們寫道:“這些影像揭示了一個意想不到的物體,介於分形和普通曲面之間:一個光滑的分形。”換句話說,他們將分形的無限性質與平滑過程相結合,以避免尖銳的脊。

圖片來源:博雷利、賈布拉內、拉扎勒斯、蒂貝爾、羅默,在他們的PNAS 論文中。
最後,“平坦”圓環看起來一點也不平坦,但它設法滿足了字面意義上的要求。所有距離都與平面上矩形上的距離完全相同。有關這種光滑分形圓環的更多資訊,請參閱 Lê Nguyên Hoang 的詳細文章、這篇文章和 Aperiodical 的 Christian Lawson-Perfect 的 影片,或關於該主題的 Numberphile 影片。
圓環還有許多其他生命:在拓撲學中,它是乘積空間的第一個例子之一,也是使用塞弗特-範坎彭定理的一個有用的首次嘗試。在動力學中,它是學生遇到的第一個平移曲面之一,並在其中玩檯球。在我的領域,泰希米勒理論中,它是唯一足夠簡單的曲面之一,你可以真正理解和計算它的泰希米勒空間。一般來說,似乎圓環通常是在遇到新想法時勝過千言萬語的例子。在感恩節的精神下,讓我們花一點時間感謝圓環,感謝它在我們遇到二維幾何或拓撲時始終是一個有用的例子。(畢竟,在可定向的虧格為一的糕點上研究數學總是更棒。)
閱讀更多我最喜歡的空間: 康託集 胖康託集 拓撲學家的正弦曲線 康託的漏帳篷 無限耳環 具有兩個原點的直線 有兩間房子的房子 法諾平面 三圓環 莫比烏斯帶 長線 空間填充曲線