2015年12月30日

我最喜歡的空間：三環面

生活在三維環面中將是自戀者的夢想。

本文發表於《大眾科學》的前部落格網路，反映了作者的觀點，不一定反映《大眾科學》的觀點

在《星際迷航：下一代》劇集“寂靜何處”中，“進取號”飛入一個虛空。為了擺脫困境，他們放下了一個固定的信標（先別管信標在太空中保持靜止意味著什麼，或者你如何讓它停留在那裡），以便更好地測量他們走了多遠。當他們飛走時，信標離他們越來越遠，直到開始靠近。最終，他們返回到了他們開始的地方。

“進取號”對虛空進行的探索不足以讓我們確定，但他們很可能意外地漫遊（或者被類神生物納吉拉姆拉入）到了一個三環面中。就像二維環面（可以表示為相對邊粘合在一起的正方形）一樣，三環面可以表示為相對面粘合在一起的立方體。當您向前或向側面移動時，您最終會在立方體的對面重新出現。當您向上移動時，您最終會在立方體的底部重新出現。

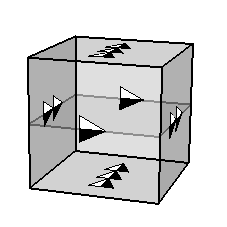
三環面的立方體模型。我們想象將匹配的箭頭粘合在一起，因此正面粘合到背面，左側粘合到右側，頂部粘合到底部。圖片來源：UIUC。

關於支援科學新聞

如果您喜歡這篇文章，請考慮透過以下方式支援我們屢獲殊榮的新聞報道訂閱。透過購買訂閱，您正在幫助確保有關塑造我們今天世界的發現和想法的有影響力的故事的未來。

二維環面很容易在許多不同的配置中想象，但三環面更難視覺化。對於二維環面，正方形圖片在某種程度上有所幫助，但甜甜圈圖片讓我更好地感受到生活在環面上會是什麼樣子。對於三環面，我沒有足夠的維度視覺化來像那樣整體地看待它。我可以嘗試透過 mentally 一次粘合一個面。首先，頂面粘合到底面，形成一個具有正方形橫截面的實心環面（基本上是一個正方形甜甜圈）。然後我們將左側粘合到右側，最終看起來像一個內部部分被吞噬的甜甜圈。但下一步是將內部粘合到外部。這在三個維度上效果不太好。

通常，當拓撲學家或幾何學家被問及她的研究的應用時，她會含糊其辭地談論宇宙的形狀，然後試圖用龐加萊圓盤的漂亮圖片來分散對方的注意力。（或者那只是我？）但三環面可能實際上與宇宙的形狀有關。拓撲學和幾何學為我們提供了對所有可能的三維形狀（也稱為三維流形）進行分類的方法。根據我們可以確定宇宙具有的屬性，我們可以縮小宇宙形狀的選擇範圍。

我不是天體物理學家，我也沒有及時瞭解可能幫助我們確定空間形狀的最新測量結果，所以我不知道目前關於宇宙形狀的想法是什麼。但如果它是一個環面呢？三環面的另一種視覺化向我們展示了生活在環面中會有多麼奇怪。

三環面的另一種視覺化。我喜歡稱之為無限腳手架。有關更大的影像，請點選此處。圖片來源：Jeff Weeks。

這個無限腳手架扭曲了三環面的一個重要特徵：三環面是有限的，而這張圖片看起來是無限的。但它更多地揭示了生活在環面中會有多麼令人迷失方向。

再次，讓我們退後一個維度，思考二維環面的類似圖片。這將是平面上的無限網格，而不僅僅是一個正方形。我們只需要記住，平面上兩個不同正方形中相對位置相同的點實際上是同一點。

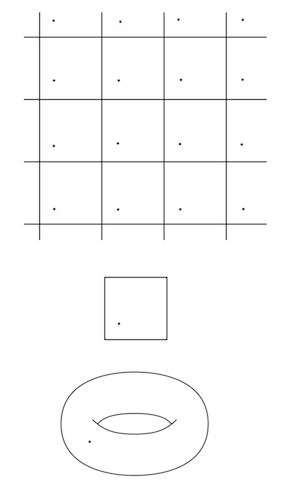
一個帶有可愛美人痣的環面以三種不同的方式描繪。頂部是作為無限晶格。每個正方形實際上都是同一個正方形。中間只是一個正方形（相對邊在腦海中粘合在一起）。底部是它作為甜甜圈形表面的實現。

如果您生活在環面（二維或三維）中，並從一個點向外看，您的視線可能會在環面上纏繞多次。

從環面中的一個點發出的線，以三種不同的方式描繪。我在二維環面中而不是三環面中繪製了這個，因為我的插圖技巧僅限於此，但您可能能夠想象在三環面的無限腳手架圖片中發生類似的事情。

如果您從三環面中的一個點直視上方，您會看到自己腳的底部。根據您的角度和視覺敏銳度，您的視線理論上可以無限次地纏繞在環面上。如果您環顧四周，您會看到無數個自己的副本。這是自戀者的夢想。

如果我們確實生活在三環面中，當然，它有點太大了，我們看不到自己的後背，這是一種解脫。不過，我想知道我們是否會永遠確切地知道我們居住的流形是什麼。