本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
每年這個時候我都會想到謝爾賓斯基三角形。
我敢說你看完那個影片之後,吃糖果玉米時不會唱“糖果玉米上校,糖果玉米上校”。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞事業 訂閱。透過購買訂閱,您正在幫助確保未來能夠繼續講述關於塑造我們當今世界的發現和想法的具有影響力的故事。
謝爾賓斯基三角形,像許多分形一樣,可以“向上”或“向下”構建。“向下”構建它,從一個實心三角形開始,然後移除中間四分之一,移除每個剩餘三角形的中間四分之一,依此類推。無限次迭代後得到的物件就是謝爾賓斯基三角形。
要“向上”構建它,建議使用糖果玉米:製作一個小糖果玉米三角形,然後製作一個三角形的三角形,然後製作一個由這些更大的三角形組成的三角形。每次迭代它都會變得更大更復雜。說謝爾賓斯基三角形是你無限重複這個過程得到的最終結果沒有太大意義,因為那樣它會蔓延到各處,但你可以想象在每個階段你拍一張照片並將其縮小,使其佔據與之前相同的空間。
除了構建謝爾賓斯基三角形的兩種直接方法外,還有許多其他過程似乎都神奇地收斂到謝爾賓斯基三角形。你可以玩一種叫做“混沌遊戲”的遊戲,並觀看隨機起點如何根據一些簡單的規則轉換為謝爾賓斯基三角形。你可以在帕斯卡三角形中為所有奇數著色,帕斯卡三角形是由包括中國和印度在內的幾種不同文化發現的,早於帕斯卡出生幾個世紀。你可以在一個大網格上繪製一個黑色方塊,然後繼續遵循稱為規則 90 的元胞自動機。
但我想考慮另一種方法,稱為謝爾賓斯基的箭頭曲線。要製作這個漂亮的形狀,你從一條鋸齒線開始。在每個步驟中,你根據一些規則,用另一條鋸齒線替換每個直線段,你可以在此圖中看到這些規則的出現。
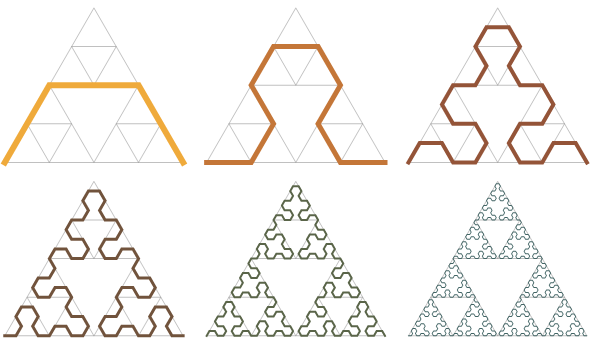
經過幾次迭代後,謝爾賓斯基三角形在這個曲線中顯現出來。 鳴謝:Robert Dickau Wikimedia (CC BY-SA 3.0)
我喜歡箭頭曲線,因為它表明,不僅可以透過在空間的移除三角形版本中削減二維形狀來接近謝爾賓斯基三角形,而且還可以透過構建一維物件來建立它。這在直覺上是有道理的:謝爾賓斯基三角形既不是完全一維的,也不是完全二維的。它實際上更像是 1.585 維的。(有關分數維度的含義的更多資訊,請檢視我關於另一個具有分數維度的物件 門格海綿 的帖子。)如果你可以透過稀釋二維物體或增肥一維物體來製作相同的物體,那麼在某種意義上,它的維度介於這兩個數字之間是有道理的。
瓦ц瓦夫·謝爾賓斯基的名字出現在一些非常好的數學物件上。除了這個美妙的三角形之外,還有一個類似形狀叫做謝爾賓斯基四面體,它存在於三維空間中。然後是謝爾賓斯基地毯,這是我幾個月前寫過的門格海綿的二維版本。最後,還有一個空間簡稱為謝爾賓斯基空間,它只有兩個點。數學研究生 Tai-Danae Bradley 最近在她的部落格 Math3ma 上寫了一篇關於為什麼這兩個微不足道的點很有趣的帖子。
那些其他以謝爾賓斯基命名的空間都非常值得尊敬,但三角形是最有萬聖節味道的。
.png?w=283)
鳴謝:Evelyn Lamb
閱讀更多關於我最喜歡的空間
康託集 胖康託集 拓撲學家的正弦曲線 康託的漏帳篷 無限耳環 具有兩個原點的線 有兩間房子的房子 法諾平面 環面 三環面 莫比烏斯帶 長線 空間填充曲線 沃利斯篩 沿狹縫粘合的兩個環面 空集 門格海綿 四個霍普夫環的連通和 博羅梅安環
