本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
你聽說過巴德爾-邁因霍夫現象嗎? 如果沒有,我相信在不久的將來你會聽到更多次。這是一種認知現象,有時被稱為頻率錯覺,它會在你第一次聽到或注意到某件事之後出現,你會突然在短時間內多次聽到它。
尼斯湖水怪空間最近讓我經歷了巴德爾-邁因霍夫現象。不久前,我偶然發現了一篇標題中就帶有這個空間的論文,顯然這個異想天開的名字吸引了我的眼球。我決定寫一篇關於它的文章,當我開始寫這篇文章時,另一位數學家在推特上談到了它。這隻有兩次,但它發生在我作為數學家的生涯中十多年從未遇到過它之後。
你可以透過在規則的二維平面上新增柄來構建尼斯湖水怪。為了建立一個數學柄,你從平面上切出兩個圓盤,並在它們之間粘上一個圓柱體。除了美觀之外,柄還使平面更易於攜帶。(也許這個空間更好的名字應該是無限手提箱或可打包平面。)如果一個柄很好,為什麼不新增更多呢?甚至無限多個?一些富有想象力的數學家決定將這個空間稱為尼斯湖水怪,因為它像極了蘇格蘭神話野獸的模糊照片。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
我不知道是否有關於奈西是變形者的傳說,但數學版本對我來說似乎就是這樣。或者也許我應該把它看作是穿著戲服。我剛瞭解尼斯湖水怪曲面,就瞭解了一些其他名字引人入勝的數學空間:雅各布天梯、無限叢林健身房和無限監獄牢房窗戶。
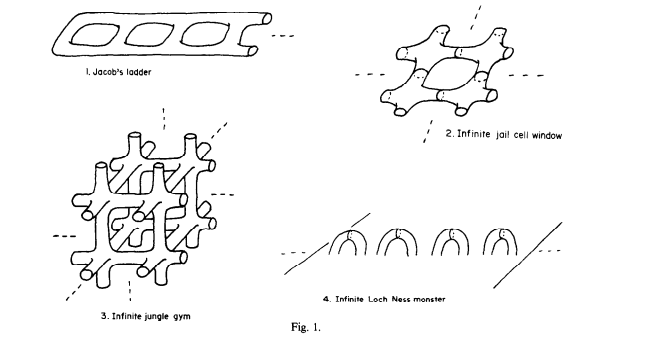
圖片來源:Ian Richards 的論文 “論非緊曲面的分類”,《美國數學學會彙刊》第 106 卷,第 2 期,1963 年。
事實證明,這四個空間在拓撲上是等價的!(當數學家、老師或作家說“事實證明”時,你應該總是抱有懷疑。他們可能正在掩蓋一些細節,而“事實證明”這句話原來是一張相當大的地毯。天哪,我又來了。)粗略地說,如果可以透過拉伸和擠壓(沒有撕裂或粘合)將一個空間變形為另一個空間,則兩個空間在拓撲上是等價的。有一個數學笑話,拓撲學家無法區分甜甜圈和咖啡杯,因為它們都有一個孔。

馬克杯和甜甜圈拓撲等價性的演示。圖片來源:Lucas V. Barbosa Wikimedia PD-self
與甜甜圈和咖啡杯不同,這四個空間的拓撲等價性對我來說一點也不明顯。叢林健身房有一個三維的感覺,而監獄牢房窗戶有一個二維的感覺,雅各布天梯更像是一維的。
最初的震驚過後,我試圖思考這三個非常不同的空間如何可能是等價的。我已經得出結論,這個空間有兩件事要告訴我:端的拓撲概念有多重要,以及我對無限空間的有限直覺的侷限性。
當我還是一名卑微的二年級研究生,並且剛剛開始閱讀我導師領域的論文時,我不斷遇到一個我不理解的詞:端。顯然我知道這個詞在英語中的意思,但它在數學上被使用,我無法理解它的數學含義。那是其中一次,我可以幾乎根據這個詞的日常含義來理解它,但又不太對勁。
在拓撲學中,當你開始談論無限曲面時,端這個詞就會出現。較小的拓撲曲面,我們稱之為緊緻曲面,有一個很好的分類:它們都是環面和射影平面的組合。事實證明(我們又來了),這些無限怪物也有一個分類,這次是基於端。
端的基本思想是,它是在曲面上走向無窮遠的一種方式,或者,如果你對“走向無窮遠”的想法沒有共鳴,那麼它就是一種遠離曲面任何有限、包含部分的方式。從一個簡單的例子開始,實數線有兩個端。如果你移除實數線的一些連通的、有限的塊,就會有兩條獨立的射線,一條向正方向延伸,另一條向負方向延伸。如果你在正方向側,你永遠無法到達負方向側,反之亦然。另一方面,二維平面只有一個端,因為如果你移除平面上某個地方的連通塊,你將能夠從平面剩餘部分的任何點到達任何其他點。
非緊曲面(如尼斯湖水怪)的分類定理(pdf)指出,如果兩個流形的某些端行為相同,則這些流形是相同的。 “行為”變得有點技術性,但基本上你需要流形具有相同的端數量、虧格(孔洞數量)和可定向性。
這就是我們如何看到我們的四個無限曲面實際上是相同的。它們都只有一個可定向的端,其中有無限多個孔洞。為了看到這一點,想象一下移除任何一個空間的某個中間部分,並想象一下使移除的中間部分越來越大。對於任何一個空間,你都可以看到剩餘部分是可定向的(你永遠不會開始在曲面上的某個地方行走,最終意外地倒著回到同一個地方),有無限多個孔洞,並且只有一個部分。換句話說,只要堅持不懈,你就可以從剩餘部分的任何部分走到任何其他部分。
不得不相信定理的話說這四個空間在拓撲上是相同的,這有點令人不滿意,但我認為我現在就是這樣。即使我可以視覺化將任何兩個具有相同孔洞數量的有限曲面相互轉換的拓撲變換,我也很難相信當我們試圖將它們推得越來越遠時,這些變換不會變得太瘋狂。就目前而言,我只能相信這個定理。但我必須承認,Spencer Dowdall 的這張將奈西描繪成雅各布天梯版本曲面的圖片有所幫助。
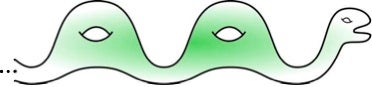
圖片來源:Spencer Dowdall
閱讀更多我最喜歡的空間: 康託集 胖康託集 拓撲學家的正弦曲線 康託的漏帳篷 無限耳環 具有兩個原點的直線 具有兩個房間的房子 法諾平面 環面 三環面 莫比烏斯帶 長直線 空間填充曲線 沃利斯篩 沿狹縫粘合的兩個環面 空集 門格海綿 四個霍普夫環的連通和 博羅梅安環 謝爾賓斯基三角形 單位正方形上的字典序 SNCF 度量 曼德勃羅集 法圖煎餅 偽球面 杜阿迪兔子 龐加萊同調球 科瓦列夫斯卡婭陀螺 一個 6 孔環面 實射影平面 一維球面