本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
當我前往聖艾夫斯時,
我遇到一個有七條線的平面,
每條線都有
七個三個點,
(但總共有七個點),
這首詩不太適合法諾平面。
我謙虛地認為法諾平面是最小的有趣空間。可能有一個厚顏無恥的歸納證明與此相反,但一個單獨的點,或幾個孤立的點,並不能構成一個有趣的例子。
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮訂閱來支援我們屢獲殊榮的新聞報道。透過購買訂閱,您將幫助確保有關塑造我們當今世界的發現和思想的具有影響力的故事的未來。 訂閱。透過購買訂閱,您將幫助確保有關塑造我們當今世界的發現和思想的具有影響力的故事的未來。
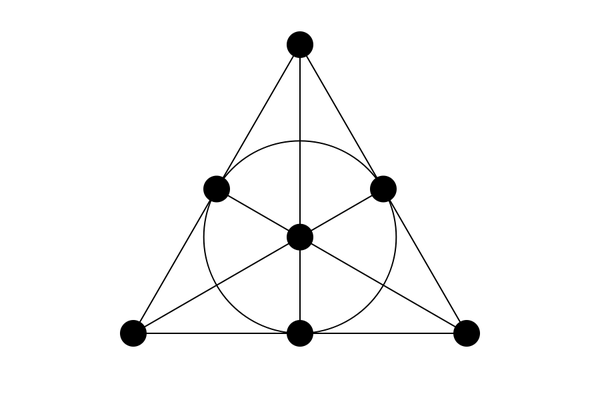
法諾平面有七個點,它們位於七條線上。僅此而已。它是射影平面最小的可能示例。
您是否曾經覺得平面上有些線相交,而有些線不相交,這有點令人掃興?多麼隨意!射影平面允許您透過強制線相交來消除這個惱人的問題。
要成為射影平面,必須滿足幾個條件。
每對點都由一條線連線。
每條線都與其他每條線相交。
存在四個點,使得沒有一條線包含其中多於兩個的點。 (第三個條件並非總是列出,但它排除了諸如一條線上有 2 個點或幾條線穿過一個點之類的愚蠢情況。)
有時數學是關於理性戰勝直覺,而當您思考射影幾何時,就是其中一些時候。(公平地說,有時射影幾何看起來非常直觀;畢竟,它的應用之一是在透視繪圖中。) 您可以透過為每組平行線新增一個“無窮遠”點,將歐幾里得平面變成射影平面。因此,水平線有一個無窮遠點,垂直線有一個點,與水平線逆時針成 47.322 度的線有一個點,依此類推。然後,您宣告無窮遠點的集合為無窮遠線。如果您思考一段時間,您可以說服自己,這滿足所有要求。
如果無窮遠線上有無限多個點對您來說太豐富了,那麼法諾平面是一個更便宜的替代方案。很容易看出點和線是如何相交和相互作用的。
法諾平面挑戰直覺。 當您看到它的圖片時,您會非常容易理解地認為它有無限多個點。畢竟,它有 7 條線,我們都知道線段,即使是非常短的線段,也有無限多個點。
不!數學是獨裁統治,而我們是獨裁者。 我們宣告這七個點是僅有的七個點。線不是由點組成的,它們只是線。 法諾平面的另一個違反直覺的方面是,其中一條線看起來像一個圓圈,至少在大多數描繪中是這樣。但是,如果您已經接受了線不是由無限多個點組成的觀點,那麼您應該不難說服自己,圓圈實際上是一條線。
法諾平面是最小的有限射影平面。您可能想知道其他射影平面有多大。如果我們想讓每條線上有 4 個點而不是 3 個,我們可以找到一個嗎?弄清楚射影平面可以有多大出乎意料地不簡單。(關於術語:法諾平面被稱為 2 階,因為每條線上有 2+1=3 個點,並且每個點都在 2+1=3 條線上。一般來說,如果每條線上有N+1 個點,並且每個點都在N+1 條線上,則射影平面的階數為N。階數為N的射影平面有N2+N+1 個點。)我們知道存在每個素數階和每個素數冪階的射影平面,但對於其他數字,我們仍然有很多工作要做。僅在九十年代 研究人員才最終證明不存在 10 階射影平面 (pdf),例如,而對於 12 階,問題仍然懸而未決。
儘管有限射影平面似乎是純粹 公理化思維戰勝任何現實暗示的勝利,但法諾平面及其親屬在賭博中(尤其是所有事物中)有一些令人驚訝的應用。我第一次在喬丹·艾倫伯格的書《How Not to Be Wrong》中讀到它們。他給出了一個彩票的例子,其中從總共 7 個數字中選出 3 個數字。玩家透過匹配所有 3 個數字或匹配 2 個數字來贏得較小的獎品來贏得頭獎。
7 個數字中選 3 個數字共有 35 種可能的組合,因此您只有 1/35 的機會贏得頭獎。但是,藉助法諾平面,您可以提高匹配 2 個數字的機會。訣竅是購買幾張彩票,並避免在任何兩張彩票上出現相同的數字對。您不想同時購買 123 和 234,因為如果兩個數字是 2 和 3,您就重複覆蓋了它兩次。這意味著獎金翻倍,但也意味著您將不會獲得不同數字對的任何獎金。
要用法諾平面贏得彩票,請用 1 到 7 的數字標記每個點,並讀出每條線上的數字。我得到了 123、147、156、246、257、345、367。
如果您檢查這些數字,您會發現每對數字都恰好出現一次。無論頭獎是什麼,我們都將至少匹配三個數字中的兩個。如果您的點標記方式與我的不同,您將獲得不同的數字集合,但它仍然具有相同的屬性。
沒有多少彩票只抽取 3 個數字,但是透過一些謹慎和計算機能力,這個想法可以擴大規模。當然,彩票支付系統不太可能有利可圖到足以證明即使是涉及射影平面的巧妙策略也是合理的,但如果您有興趣,艾倫伯格講述了 Cash WinFall 的故事,該彩票的獎金足以讓一些麻省理工學院的學生贏得一些真金白銀。
要了解法諾平面、拉丁方、環面拓撲、糾錯碼和許多其他主題之間的聯絡,請檢視弗吉尼亞理工大學的以斯拉·布朗的這兩篇文章:(7,3,1)的眾多名稱 和 (7,3,1)的更多名稱。如果您喜歡的話,法諾平面還可以幫助您記住八元數中的乘法運算方式,並且我忍不住指出它與死亡聖器的符號驚人地相似。

公理幾何學對石頭、魔杖或隱身衣幾乎無話可說。圖片:公共領域,來自 維基共享資源。
閱讀更多我最喜歡的空間: 康託集 胖康託集 拓撲學家的正弦曲線 康託的漏帳篷 無限耳環 具有兩個原點的線 具有兩個房間的房子 環面 三環面 莫比烏斯帶 長線 空間填充曲線