2018年1月31日

我最喜歡的空間之幾：懸鏈面

慶祝可能是最簡約的最小曲面

本文發表於《大眾科學》的前部落格網路，反映了作者的觀點，不一定反映《大眾科學》的觀點

有點尷尬的是，我已經寫我最喜歡的空間快三年了，但還沒有包括任何最小曲面。我的導師Mike Wolf 研究最小曲面。雖然我最終沒有進入那個研究領域，但我學到了一些基礎知識，並且當我與我的學界同仁談論他們的工作時，這個話題有時會被提及。所以這篇文章早就應該寫了。

最小曲面的概念是，如果你給定一個邊界曲線，那麼就存在一個面積最小的曲面，其邊緣就是該邊界曲線。（這被稱為普拉託問題，以物理學家約瑟夫·普拉託的名字命名，而不是因為曲面看起來像高原。）數學家和普拉託本人特別喜歡用肥皂泡作為例子。如果你從肥皂泡的金屬絲框架開始，肥皂通常會呈現出一種形狀，使以該金屬絲邊界為邊界的薄膜面積最小化，正如 Henry Segerman 在這段影片中演示的那樣。

關於支援科學新聞事業

如果您喜歡這篇文章，請考慮透過以下方式支援我們屢獲殊榮的新聞事業訂閱。透過購買訂閱，您正在幫助確保未來能夠繼續講述關於塑造我們當今世界的發現和思想的有影響力的故事。

如果您想更深入地瞭解肥皂薄膜和最小曲面，請檢視我的導師就此主題所做的演講。今天，術語“最小曲面”指的是任何在區域性最小化面積的曲面。“區域性”一詞意味著，如果我們觀察曲面上任何點周圍的小區域，就沒有辦法減少該小區域的面積。這首先意味著我們不再需要在曲面上有一個邊界。但是，也存在一些邊界，允許多個不同的區域性面積最小化曲面跨越它們，正如 Segerman 在影片中演示的那樣。

懸鏈面是在微分幾何課程中您將遇到的最早的最小曲面之一。如果您想用肥皂薄膜製作一個，您需要將邊界製成兩個彼此平行且相隔很短距離的圓。

肥皂薄膜懸鏈面。圖片來源：Blinking Spirit *Wikimedia*

懸鏈面也是透過繞軸旋轉稱為懸鏈線的曲線而獲得的旋轉曲面。（懸鏈線本身就很有趣，但那是另一個部落格帖子的故事了。）

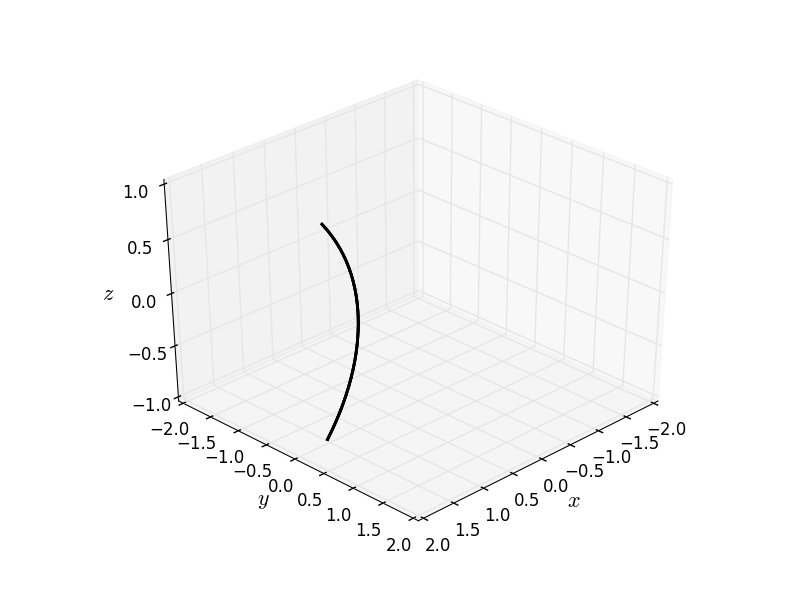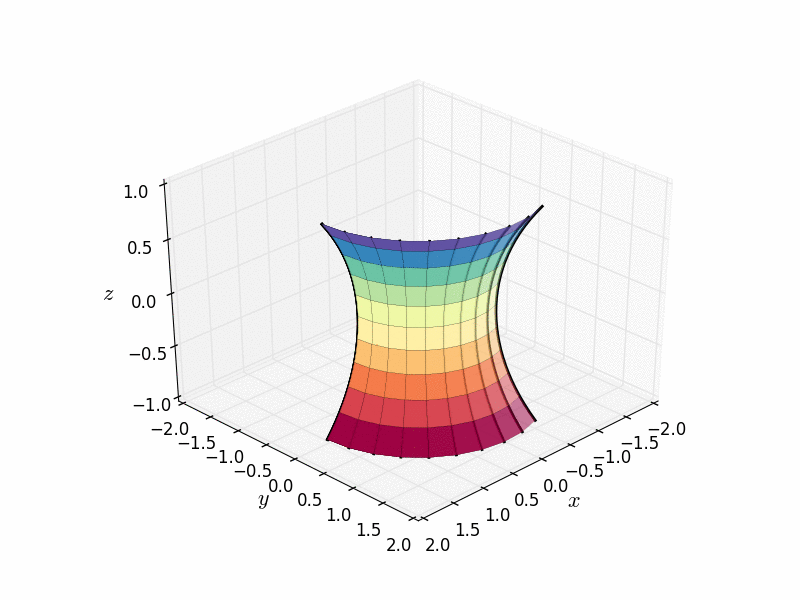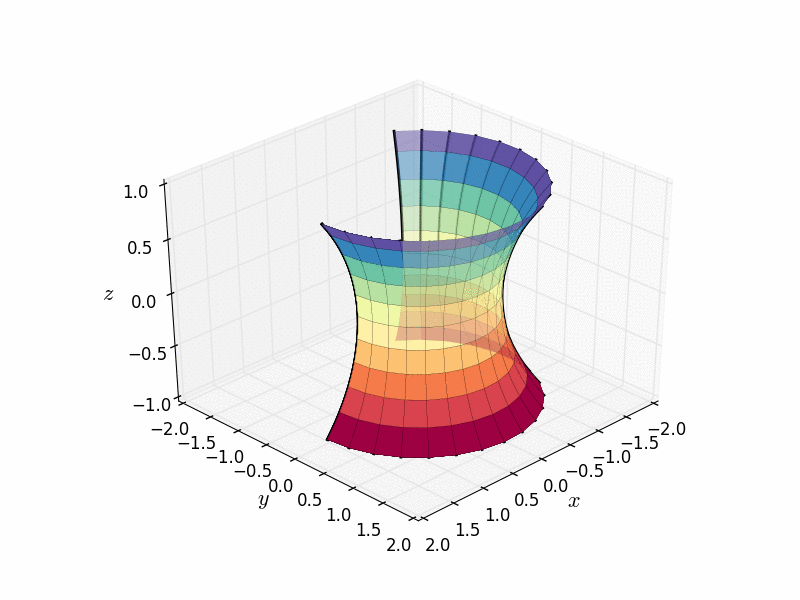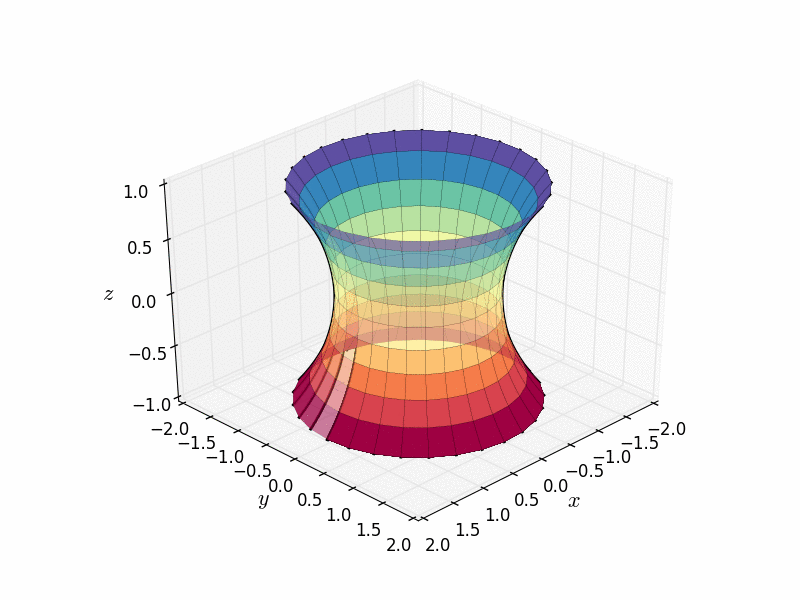
由懸鏈線作為旋轉曲面建立的懸鏈面。圖片來源：Nicoguaro *Wikimedia*(CC BY 4.0)

您可能會聽到懸鏈面被稱為“細腰圓柱體”，因為它像許多人的腰部一樣向中間收縮。（我喜歡想象年輕的懸鏈面在談論他們上週末是多麼的“細腰”。）

透過檢查懸鏈面，我們可以開始注意到最小曲面的另一個特徵。首先，我們可以看看當我們將兩個邊界圓彼此移開時，肥皂薄膜懸鏈面會發生什麼變化，如本影片所示。

一開始，懸鏈線只是略微彎曲。它幾乎是一個規則的圓柱體。但是隨著圓圈的移動，腰部變得更加明顯。（最終，沒有足夠的肥皂薄膜來維持懸鏈面，因此它會破裂並塌陷以填充兩個圓圈，但從數學上講，我們將專注於它在懸鏈面構象中花費的時間。）在整個過程中，我們可以觀察曲率如何變化。我在“我最喜歡的定理”Jeanne Clelland 那一集的節目註釋中寫了關於曲率的內容。在懸鏈面中，我們將觀察連線兩個邊界圓的曲線的曲率和圍繞懸鏈面腰部的曲線的曲率。

當圓圈之間執行的曲線更接近平坦時，腰部曲線也更接近平坦。當圓圈分開並且它們之間的曲線更彎曲時，腰部也變得更彎曲。碰巧的是，這兩條曲線，一條從中點“向上”彎曲，另一條“向下”彎曲，總是完美地相互平衡。這不僅僅是碰巧適用於懸鏈面的巧合。事實證明，具有此屬性的曲面（稱為具有恆定平均曲率零）是表徵最小曲面的另一種方式。在某些地方，它們可能非常彎曲，而在某些地方則更平緩地彎曲，只要曲率完美平衡即可。

懸鏈面本身是一種非常對稱、可愛的形狀，但它還有另一種超能力。只需剪開一刀並進行一些小心的操作，它就可以在不拉伸或擠壓的情況下轉變成（部分）螺旋麵，另一種最小曲面。

懸鏈面和螺旋麵之間的轉換。圖片來源：Wickerprints *Wikimedia*

1776 年，懸鏈面和螺旋麵是被證明是最小曲面的第一個非平凡曲面。（平面或其一部分是平凡的例子。）自那以來的幾個世紀裡，數學家們發現了一系列越來越奇異的最小結構，它們具有奇特的自相交、重複部分或孔洞。但就優雅的簡潔性而言，懸鏈面是無與倫比的。