本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定代表《大眾科學》的觀點
n個圓的花束在我心中佔有特殊的地位。我想我應該說n個圓的花束們在我心中佔有特殊的地位,因為對於每個整數n,都存在這樣一個花束。這個空間也被稱為n個圓的楔形或n個花瓣的玫瑰(儘管它通常看起來更像雛菊),它由n個在一點相遇的圓組成。我們從拓撲學的角度考慮這個空間,其中確切的形狀和距離並不重要,所以在圖片中,“圓”通常會稍微變形。否則,當我們試圖在平面上繪製它們時,它們會重疊。
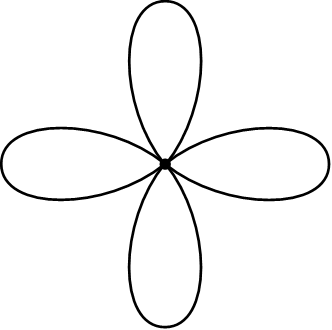
一個由4個圓組成的花束。來源:Jim Belk,維基共享資源
我如此喜愛這個空間的原因是,它是拓撲學產生代數洞察力的一個例子。代數,基本上是對稱性和結構的研究,是拓撲學中一個非常有用的工具,但拓撲學在代數中應用的情況比較少見。為了理解原因,我們需要研究基本群。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關當今塑造我們世界的發現和想法的具有影響力的故事的未來。
基本群是拓撲學家用來區分和描述空間的一個根本重要的工具。基本群描述了您可以在空間中繪製的環的種類。如果可以透過在空間中擺動一個環使其與另一個環重合,則認為兩個環是相同的。磁碟或平面中的任何兩個環都可以透過這種方式等價,因此它們的基本群非常無聊。但是在像環面(甜甜圈的表面)這樣的空間中,存在一些不能相互擺動的環,並且基本群具有更多的意義。
在n個圓的花束中,可以透過環繞的圓、方向、次數和順序來識別環。例如,在由2個圓組成的花束(即數字8)中,有一個環,它順時針繞左邊的圓一次,然後繞右邊的圓一次。這個環與繞右邊的圓然後繞左邊的圓的環不同,因為空間中沒有空間讓您操作一個環並將其變成另一個環。(您可以使用橡皮筋來說服自己這個事實。)在下圖中,順時針繞左邊圓的環標記為a,逆時針繞右邊圓的環標記為b,我們定義a-1(發音為“a的逆”)為逆時針繞左邊圓的環,b-1為順時針繞右邊圓的環。
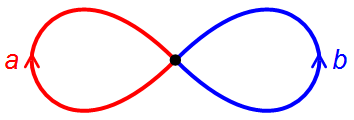
一個數字8,或由2個圓組成的花束。來源:Jim Belk,維基共享資源
數字8的基本群可以用a、a-1、b和b-1的所有有限字串表示。(您應該稍微懷疑我偷偷地加入“有限”這個詞,因為我從未告訴過您環的嚴格定義要求它具有有限的長度。現在我說了。)如果a旁邊出現a-1,或者b旁邊出現b-1,您可以將它們抵消。
描述數字8的基本群的精巧方法是由2個生成元生成的自由群。生成元是字母a和b,它們自動帶有它們的逆元,而單詞“自由”指的是,除了將一個字母放在它的逆元旁邊,沒有其他方法可以抵消任何相鄰出現的字母組合。有些群可以發生這些抵消,但自由群不是發生這些抵消的地方。
正如數字8的基本群是兩個生成元上的自由群一樣,n個圓的花束的基本群是n個生成元上的自由群。在您使用這些花束來證明一個關於自由群的非常酷且至少對我而言是違反直覺的事即時,它似乎很普通:3個生成元上的自由群是2個生成元上的自由群的子群!更一般地說,n個生成元上的自由群是2個生成元上的自由群的子群。這對我來說是違反直覺的,因為看起來3個生成元應該比2個生成元給出“更大”的群,並且子群看起來比它們所屬的群“更小”。但是當涉及到像自由群這樣的無限事物時,這些直觀的概念通常會被拋到九霄雲外。
抱歉,拓撲學學生們,我不會告訴您如何使用圓的花束來證明3個生成元上的自由群是2個生成元上的自由群的子群。但是,一旦您掌握了正確的定理,這就是代數中一個事實的證明實際上從拓撲設定中出來的非常酷的例子。(這些定理做了很多繁重的工作來連線代數和拓撲學,所以它不是憑空產生的,但我仍然認為它非常酷。)
我在研究生院努力通過了拓撲學資格考試。(資格考試或初試是大多數研究生課程要求學生在正式進入學位研究和論文部分之前透過的考試。通常,學生應在研究生課程的第一年或兩年內透過考試。)由於這種掙扎以及我花費在這些材料上的額外時間和精力,這可能是我今天仍然可以透過的唯一資格考試!考試前一晚我學習的最後一件事是教科書末尾關於自由群和n個圓的花束的一節。我認為我們在課堂上講過這個材料,但當時沒有記住。這可能是我第n次閱讀該部分並試圖理解它的一個相當大的n,但這次不同。我不認為天堂真的打開了,但我確實記得當我最終真正理解了本節中的大思想時,那種頓悟和輕鬆的感覺。第二天早上,考試碰巧有兩個關於我剛剛學習過的材料的問題。我感到非常幸運,在晚上合上書本之前剛好學習了正確的東西,從那時起我就一直對圓的花束心存感激。
閱讀更多我最喜歡的空間: 康託集 胖康託集 拓撲學家的正弦曲線 康託的漏帳篷 無限耳環 具有兩個原點的直線 具有兩個房間的房子 法諾平面 環面 三環面 莫比烏斯帶 長直線 空間填充曲線 瓦利斯篩 沿縫隙粘合的兩個環面 空集 門格海綿 四個霍普夫鏈環的連通和 博羅梅安環 謝爾賓斯基三角形 單位正方形上的字典序 SNCF 度量 曼德勃羅集 法圖煎餅 偽球面 杜阿迪兔 龐加萊同調球面 科瓦列夫斯卡婭陀螺 一個有6個孔的環面 實射影平面 一維球面 尼斯湖怪 科赫雪花 雙圓柱 懸鏈面 SO(3) 偽菱形立方八面體 莫澤錠子 阿涅西的女巫 安託萬項鍊