2017年12月30日

我最喜歡的空間：雙圓柱體

這種形狀也被稱為牟合方蓋或斯坦梅茨立體，最早在中國對球體體積的探索中出現

雙圓柱體，牟合方蓋，或斯坦梅茨立體。

Ag2gaeh Wikimedia(CC BY-SA 4.0)

本文發表於《大眾科學》的前部落格網路，反映了作者的觀點，不一定反映《大眾科學》的觀點

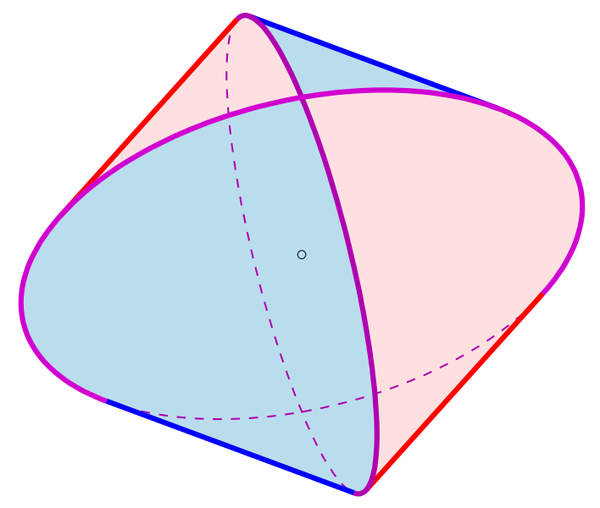
雙圓柱體是一個可愛的小形狀。它有正方形的橫截面，但仍然令人愉悅地彎曲。它是你觀察兩個相同的實心圓柱體以直角相交時得到的形狀。早期的中國數學家稱這種形狀為牟合方蓋，有時翻譯為“兩個方形雨傘”，它也被稱為斯坦梅茨立體。（人們也使用術語斯坦梅茨立體來指代由三個或更多，而不是兩個，相交圓柱體構成的類似圖形。）

一個動畫展示了從兩個相交圓柱體中出現的雙圓柱體。來源：Van helsing *Wikimedia*(CC BY-SA 3.0)

這個物體出現在我最喜歡的卡瓦列裡原理的例子中。卡瓦列裡原理是指如果兩個物體在每個高度的橫截面積相同，則這兩個物體具有相同的體積。（當然，有一些技術細節需要理清，以確保我們正確地測量橫截面。）當你口頭表達這個想法時，它似乎是顯而易見的，但當你在實際中看到它時，可能會違反直覺。微積分老師喜歡用一堆硬幣作為例子。你可以將它們整齊地排列成一個完美的圓柱體，或者用它們建造一個搖搖晃晃的塔。無論哪種方式，這都是同一堆硬幣，所以這兩個塔具有相同的體積。

關於支援科學新聞報道

如果您喜歡這篇文章，請考慮透過以下方式支援我們屢獲殊榮的新聞報道訂閱。透過購買訂閱，您正在幫助確保未來能夠繼續講述關於發現和塑造我們當今世界的想法的有影響力的故事。

一個非常英式的卡瓦列裡原理演示，使用了英鎊硬幣。這兩個塔有不同的形狀，但體積相同。（而且成本也相同。）來源：Chiswick Chap *Wikimedia* (CC BY-SA 3.0)

你不是每天都能在計算中使用卡瓦列裡原理，所以它總是感覺有點特別。Vsauce有一個關於餐巾環問題的有趣影片，這是該技術的一個令人驚訝的應用。

我最喜歡的關於雙圓柱體的故事始於劉徽，一位生活在公元三世紀的中國數學家。他今天最出名的是他對《九章算術》（一部重要的早期中國數學著作）的廣泛註釋，以及他的使用內接多邊形計算π的演算法。劉徽使用了雙圓柱體，或者當他研究球體的面積時。

思考球體的一種方式是將其視為一堆彼此堆疊的無限薄的圓片。最大的圓片在正中間，越靠近兩極，圓片越小。

薄圓片構成一個球體。要製作雙圓柱體，請將每個圓片替換為正方形。來源：伊芙琳·蘭姆

要獲得雙圓柱體，只需將每個薄圓片替換為一個外接正方形。據我所知，劉徽是以這種方式提出雙圓柱體的，他尋找的是一個包含球體的形狀，而不是透過觀察兩個圓柱體的交集。但是，不難說服自己，這堆正方形與兩個圓柱體的交集是相同的。首先，想象一下將一個球體放在雙圓柱體的中間。現在想象一下，沿垂直於兩個圓柱體的方向切割雙圓柱體的橫截面。每個橫截面都將有一個雙圓柱體的正方形外接球體的一個圓。（如果你難以想象，你可以隨時拿起幾個衛生紙捲筒，製作自己的雙圓柱體。）

像劉徽一樣，我們現在可以注意到，牟合方蓋的橫截面始終是一個外接圓的正方形。如果我們稱圓的半徑為r，我們可以得出結論，雙圓柱體與球體的每個橫截面的面積比為4r²:πr²，或4:π。現在，卡瓦列裡原理意味著這兩個物體的體積比也為4:π。

今天，這感覺就足夠了。球體的體積公式是眾所周知的，所以我們可以從那裡開始。如果一個球體的體積為4/3πr³，我們可以得出結論，雙圓柱體的體積為16/3r³。* 但這不是劉徽的起點。他實際上試圖使用雙圓柱體來獲得球體的面積公式。不幸的是，他在那裡卡住了。但這絕非小小的進步。正如林力揚和沈康身在一篇關於中國卡瓦列裡原理應用的論文中寫道：“儘管劉徽承認他無法繼續證明球體的體積，但他已經用數學的嚴謹性分析了這個問題，並確定了困難的領域。” 在劉徽去世約200年後，祖沖之和他的兒子祖𣈶能夠在他停下的地方繼續前進，並使用雙圓柱體完成了球體體積的計算。他們的方法涉及對雙圓柱體的外接立方體的巧妙分解。

有關劉徽、祖沖之和祖𣈶在確定球體體積方面的工作的更多資訊，請檢視林力揚和沈康身的“中國卡瓦列裡原理的概念及其應用”或T. Kiang的“一種古老的中國球體體積計算方法”。（前者似乎可以免費訪問；後者可能需要付費。）您還可以透過Anthony Or的一些Geogebra工作表探索雙圓柱體，其中一個工作表展示了一些立方體分解。

*本句已編輯以更正雙圓柱體體積中的錯誤。