我最喜歡的一些空間：康託的漏帳篷

本文發表於《大眾科學》的前部落格網路，反映了作者的觀點，不一定反映《大眾科學》的觀點

我必須承認，在寫關於 π-Base（一個收集有趣數學空間資訊的網站）之前，我並不知道康託的漏帳篷。它的名字非常奇特有趣，以至於我不得不瞭解更多關於它的資訊。在閱讀關於漏帳篷之前，您可能需要熟悉康託集——幸運的是，我在三月份寫過關於它的文章。

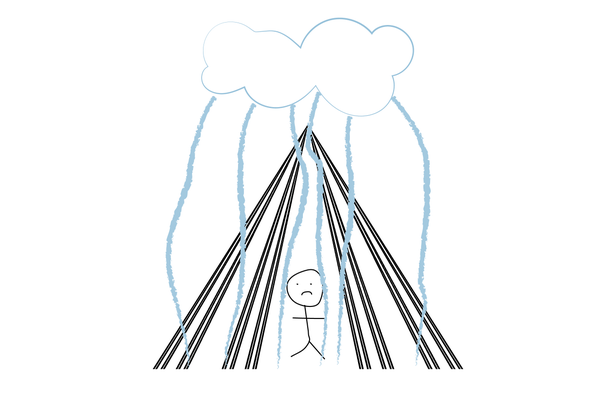
為了構造康託的漏帳篷，有時也稱為 Knaster-Kuratowski 扇，您首先需要將康託集放在歐幾里得平面的 x 軸上，並新增點 p=(1/2,1/2)。然後，您用直線將康託集中的每個點連線到點 p。此時，我們有了一個漂亮的防水帳篷。

現在我們在上面戳洞。康託集中有兩種型別的點。一些點，如 0、1/3 和 1，是被移除區間的端點，而另一些點，如 1/4，則不是。我們將分別考慮這兩種型別的點。對於康託集中的每個點 x，我們都有一條連線 x 到 p 的線。我們將修改這些線。

支援科學新聞報道

如果您喜歡這篇文章，請考慮訂閱以支援我們屢獲殊榮的新聞報道。 訂閱。透過購買訂閱，您將幫助確保未來能夠繼續講述關於塑造我們當今世界的發現和想法的具有影響力的故事。

如果 x 是一個端點，我們只考慮線上 y 座標為有理數的點。如果 x 不是端點，我們只考慮線上 y 座標為無理數的點。現在，從康託集到 p 的每條線都已被完全打碎。

令人驚訝的是，我們並沒有只剩下平面上散落的點。康託的漏帳篷是連通的。

要定義一個空間連通意味著什麼出乎意料地困難，但當我在寫關於拓撲學家的正弦曲線時，我嘗試過。基本上，如果我們找不到兩個集合 A 和 B，使得空間的一部分在 A 中，一部分在 B 中，並且空間 A 和 B 不重疊，那麼該空間就是連通的。（我們還需要一個技術條件，即 A 和 B 是開集，這意味著在每個集合中的每個點周圍，都有一個也位於該集合中的“blob”。如果您想了解更多詳情，請檢視上個月的帖子。）

我們在康託的漏帳篷上戳了很多洞，所以它看起來肯定應該是斷開連線的。如果您試圖從康託集中的一個點走到點 p，您是無法做到的。但不知何故，這還不太夠。

康託的漏帳篷是連通的完整證明非常複雜，所以我在這裡留下一個連結供勇敢的讀者參考。我思考這個問題的方式是從嘗試將帳篷放入兩個獨立的開集 A 和 B 開始。點 p 很特殊，所以我首先處理了它。它必須在集合 A 或集合 B 中，所以不妨設它在 A 中。然後因為 A 和 B 都是開集，所以在 p 周圍必須有一個完全位於 A 內的“blob”。這個“blob”必須包含來自所有線的點，所以某些線上必須在某處有一些過渡點，這樣一些線才能在 B 中有點。準確地找出哪裡出了問題是樂趣（和挑戰）所在。

康託的漏帳篷是連通的，但只是勉強連通。頂部點 p 就像掛在毛衣上的線：如果您拉一下它，整個東西就會散開。當我們移除 p 時，集合不僅變得斷開連線，而且變得儘可能地斷開連線。您可以很容易地將其分成兩個不相交的部分：其中一部分包含 x 座標小於 1/2 的點，另一部分包含 x 座標大於 1/2 的點。但它甚至更混亂：新集合（有時稱為康託帳篷）中沒有兩個點在同一個連通部分中。對於任意兩個點，您總能找到一種方法將康託帳篷分成子集，使這些點彼此分離。康託的漏帳篷只有一個連通部分，但康託帳篷有無限多個，而且它們只是單個點。如果您對術語感興趣，p 被稱為離散點，而沒有任何大於一個點的連通部分的集合被稱為完全不連通。

如果康託的漏帳篷對您來說還不夠，那麼還有一個相關的空間叫做康託的更漏的帳篷，它顛倒了有理數和無理數的高度。即使有理數和無理數的集合都是無限的，但無理數更多，因此這些集合並非完全可互換。在康託的漏帳篷中，康託集的可數個端點與線上到 p 的可數個有理點配對。更漏的帳篷將可數個端點與不可數個無理點配對，並將不可數個非端點與可數個有理點配對。這種不匹配足以在很大程度上改變某些屬性，並證明了嚴格證明對數學家的重要性。我上面概述的論點似乎適用於這兩個集合，但雖然漏帳篷是連通的，但更漏的帳篷不是。要了解更多關於康託的更漏的帳篷的資訊，請檢視這個 Math Stackexchange 帖子。

閱讀更多關於我最喜歡的空間： 康託集 胖康託集 拓撲學家的正弦曲線 無限耳環 具有兩個原點的直線 具有兩個房間的房子 法諾平面 環面 三環面 莫比烏斯帶 長線 空間填充曲線