2017年7月31日

我最喜歡的空間：一個六孔環面

一切都從一個五邊形開始...

本文發表於《大眾科學》的前部落格網路，反映了作者的觀點，不一定反映《大眾科學》的觀點

在我的上一篇文章中，我寫了如何將“展開”一個矩形檯球桌變成環面，或者說是一個百吉餅或甜甜圈的表面。這篇文章是閱讀本文的良好背景。矩形是展開多邊形以獲得表面的一個簡單例子。它的四個角拼合在一起，總共達到完美的 360°，這使得它幾乎太簡單了。我想看看我是否真的理解了如何透過嘗試另一個例子來展開臺球桌。

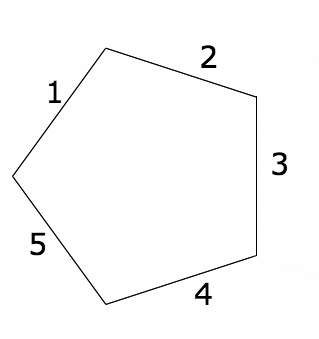
當瑪麗安·米爾扎哈尼在 2014 年贏得菲爾茲獎時，我驚訝地發現，關於她和另一位菲爾茲獎得主阿圖爾·阿維拉的作品的影片中都出現了五邊形中的檯球（在 Quanta 關於米爾扎哈尼的影片中1 分 20 秒處和關於阿維拉的影片中1 分 00 秒處）。所以幾天前，我決定展開一個五邊形檯球桌，看看它會形成什麼表面。

關於支援科學新聞報道

如果您喜歡這篇文章，請考慮透過以下方式支援我們屢獲殊榮的新聞報道訂閱。透過購買訂閱，您正在幫助確保有關當今塑造我們世界的發現和想法的具有影響力的故事的未來。

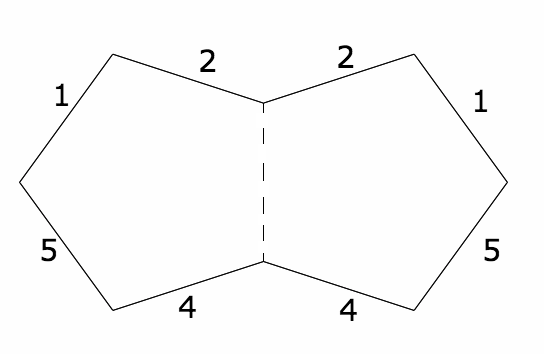
我們可以展開五邊形的一種方法是沿著五邊形上的軌跡，就像我們對矩形所做的那樣。但這真的沒有必要。沿著一個點的軌跡繞圈走的重要之處在於，最終我們看到了矩形以每種可能的方式旋轉和反射，從而保留了它的頂點。所以我從一個單獨的五邊形開始，並標記了邊緣以幫助我記賬。然後我沿著一條邊展開它，並記錄了哪些標籤去了哪裡。

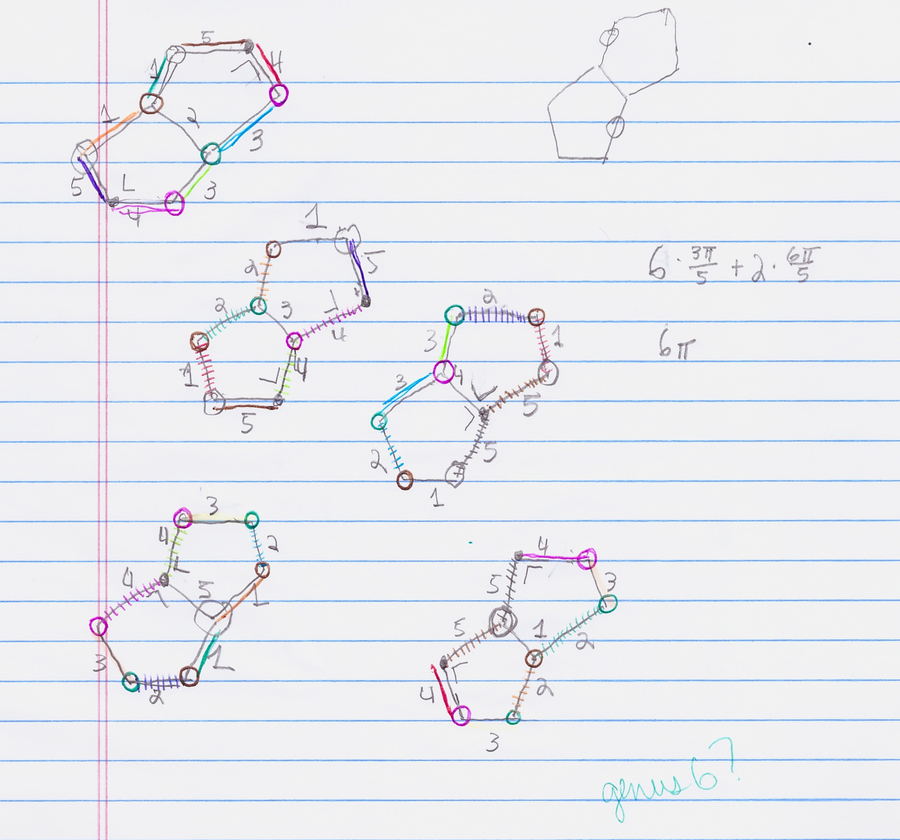
然後我重複這個過程，直到我沿著每個可能的邊緣都反射了它。我的作品比上面的計算機生成影像要凌亂一些。我用紙和一堆彩色筆和鉛筆在紙上完成了它。它沒有像米爾扎哈尼巨大的紙質塗鴉那樣宏大，但它對我來說很有效。最後，我有五個雙五邊形的副本。（還有一點草稿。）

將矩形轉換為環面很容易視覺化。將五個八邊形集合與一堆標記的邊緣一起，並弄清楚當您將所有邊緣粘合在一起時，甜甜圈將有多少孔，這有點不太直接。

我記錄了標籤，並且知道應該將哪些邊緣粘合在一起，但我還需要一個成分來計算我的表面中的孔數：高斯-博內定理。

高斯-博內定理是一個神奇的定理（不完全是我最喜歡的，但也很接近），它將曲面的曲率與其拓撲結構聯絡起來。它部分指出，多孔甜甜圈的總曲率為2π(2-2g)，其中g是虧格，或表面具有的孔數。因此，只有一個孔的甜甜圈的總曲率為 0。當然，曲率有一個技術定義，但將其視為表面彎曲的程度就可以了。平坦的東西曲率為 0，像球體一樣圓形的東西具有正曲率，而像馬鞍形一樣的東西具有負曲率。

在我們的例子中，我們展開的多邊形是完全平坦的。因此它們的表面不會對總曲率產生任何貢獻。但是當我們把它們粘合在一起時，我們會得到一些頂點，它們的周圍角度超過 360°。曲率就在這裡。當我們把矩形粘合在一起時，我們很幸運，四個直角加起來正好是 360 度。在雙五邊形的情況下，稍微多記一些賬就可以看出，我們在表面上有 5 個奇怪的點，每個點的周圍角度為 1080°（6π 弧度）。這些點有點像停車場：如果你一直繞著其中一個點轉，你旋轉 360° 後不會回到你開始的地方。

由於原因需要比這篇博文更長的時間來解釋（你只需要相信我的話），每個特殊點周圍的超額角度（即，超過 360 度或 2π 弧度的量）會影響表面的總曲率。（它帶有一個負號，因為它使表面更具負曲率，像馬鞍而不是球。）因為五邊形是平坦的，所以所有曲率都存在於頂點處，所以我們可以使用高斯-博內定理，以及對錶面有多少超額角度的計算，來計算其虧格。五個奇怪的點每個都對錶面貢獻了 720°（4π 弧度）的負曲率。總共為 -20π。將其代入高斯-博內定理，我們看到 2π(2-2g)=20π。我們可以消除每邊的幾個因子，得到 2g-2=10，因此 g=6。

當我最終使計算結果成立時，我真的很高興。當我查閱一些檯球參考文獻並發現我做對了時，我更加興奮！有關多邊形中臺球的更多資訊，請檢視這些參考文獻
檯球和平面，作者：戴安娜·戴維斯（Diana Davis）（面向數學背景較少的人）
檯球的共形幾何，作者：勞拉·德馬科（Laura DeMarco）（面向數學家）

就是這樣！五邊形展開成一個虧格為 6 的表面，或一個六孔環面。即使一個單獨的五邊形看起來與像那樣大的複雜表面相去甚遠，但粒子在任一表面上的流動行為都是相同的。分析一個可以解釋另一個表面上發生的事情。我必須承認，我看不出展開的五邊形粘合在一起作為虧格為 6 的表面會是什麼樣子，但我無論是否可以視覺化它，都能夠進行分析。話又說回來，我可能不得不拿出一些布料和線，為埃莉 L 形桌子製作一個同伴，埃莉是我最喜歡的柔軟而<0xC2><0xA0>有彈性的虧格為 2 的表面。