本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
配偶:你這個月最喜歡的空間是什麼? 我:我還不確定。有什麼建議嗎? 配偶:嗯,這個月是我的生日。你可以做一個平面。 我:我應該做哪一個? 配偶:哦,哦,做兩個沿狹縫粘合在一起的環面!我喜歡那個! 因此,本月最喜歡的空間獻給我的好配偶。生日快樂!
我的配偶的研究領域位於幾何學和動力系統的交叉點。幾何學是不言自明的:形狀、距離。動力系統,或動力學,是研究隨時間變化的空間的學科。
我的配偶研究的系統型別之一是多邊形中的檯球。典型的例子是矩形中的檯球,這正是實際檯球遊戲的玩法。數學家忽略了摩擦或球桌不規則性的影響,並以理想化的方式思考檯球。不是具有質量的球,而是一個單點沿直線移動,直到撞擊球桌的側邊,此時它與側邊發生完全彈性碰撞,並沿另一個方向繼續前進。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保關於塑造我們當今世界的發現和思想的具有影響力的故事的未來。
但即使那樣對於數學家來說也太多了!所有這些彈跳和改變方向使得跟蹤軌跡變得過於複雜,因此他們採用了一個巧妙的技巧來簡化他們的問題:他們展開球桌。當球撞擊側邊時,不是球被反射,而是球桌被反射,球繼續不受阻礙地前進。這樣,方向永遠保持不變。為了瞭解這對於矩形是如何工作的,我們將跟隨一個點周圍,看看會發生什麼。
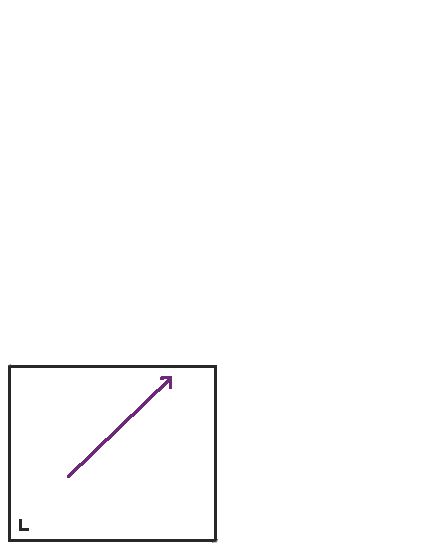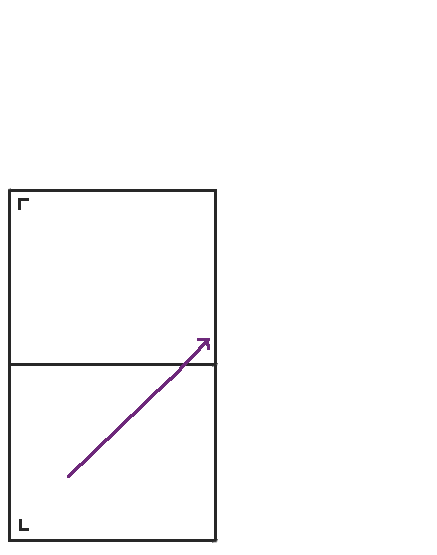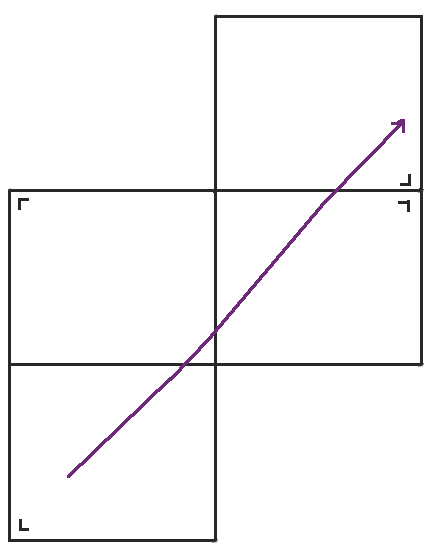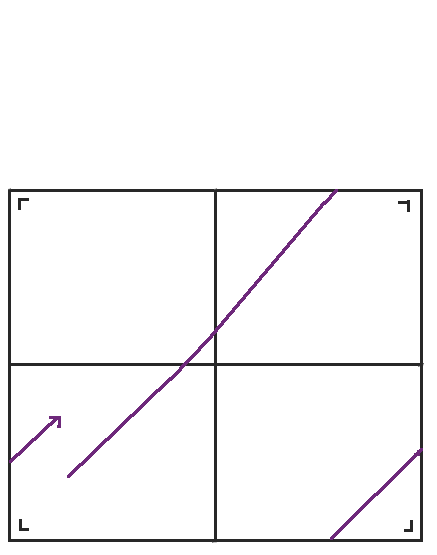
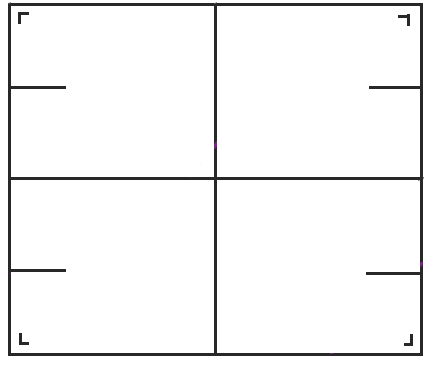
首先,我們從矩形中向東北方向移動開始。我在左下角用一個小 L 標記了矩形,以便我們可以跟蹤當我們展開球桌時球桌的方向。
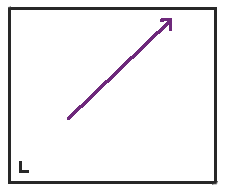
當我們到達矩形的頂部時,不是彈回,而是將球桌沿頂部反射,並且點繼續前進。
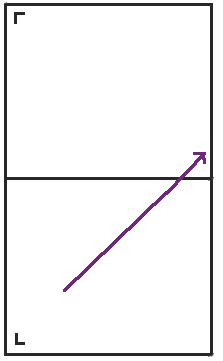
當我們到達球桌的右側時,我們將球桌沿右側反射並繼續前進。

當我們到達那個球桌的頂部時,我們再次反射。
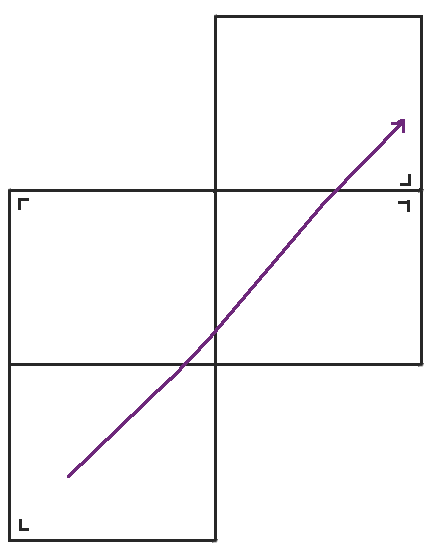
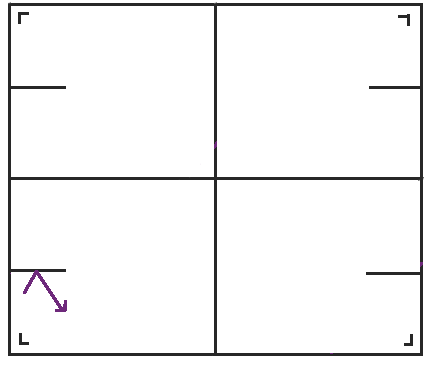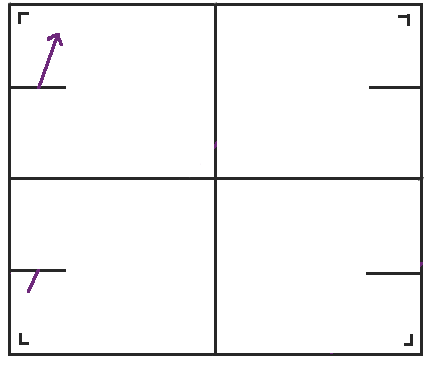
當我們到達右側時,我們可以再次反射球桌,但是左下角的球桌與我們將要得到的球桌具有相同的方向,所以我們不妨再次跳回到左下角的球桌。當我們稍微重新排列球桌時,我們得到了我們熟悉的環面,一個頂部粘到底部,左側粘到右側的矩形。

這是整個過程的 gif 動畫。
透過這種方式,矩形中的檯球與環面上的直線流直接相關,而直線流更容易研究。西北大學數學家戴安娜·戴維斯有一篇關於數學臺球的精彩的科普論文 (pdf),其中提供了更多關於多邊形中的檯球和曲面上的直線之間關係的資訊。
我的配偶非常喜歡矩形上的檯球,但那裡的軌跡行為已經被很好地理解了,所以他想要更大的挑戰。使曲面複雜化的最簡單方法是向其新增障礙物。想象一下,某個不體諒他人的人將他們的球杆釘在了球桌上,並且球除了側邊之外還從球杆上彈開。
我們可以像對矩形所做的那樣進行相同的展開程式來獲得這張圖片。
但現在我們需要小心。我們希望檯球軌跡都是直線的,而不是彈跳和改變方向,因此當我們撞擊障礙物時,我們需要跳到障礙物的另一個副本並沿相同的方向繼續前進。這樣,它變得更像一個狹縫或蟲洞——你從一側掉進去,然後從另一側出來。
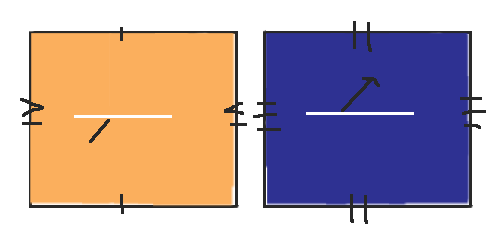
現在我們遇到了一個有趣的困境。我們可以將左右兩側粘合在一起,沒有問題,但是狹縫將圖形分成兩個圓柱體。我已經將一個塗成藍色,另一個塗成橙色。

在這一點上,我們可以完全重新概念化圖形,以獲得我的配偶非常喜歡的空間,即沿狹縫粘合在一起的兩個環面。球桌上的狹縫應該粘合在一起,使每個圓柱體成為一個單色的環面,其中一側的一部分實際上沒有粘合在一起。然後你可以拖動未粘合的部分,使其更容易看到,就在環面的正中間。我已經用二維方式將其描繪為兩個帶有識別線繪製的矩形——你將匹配的線粘合在一起——但你也可以在三維中將其視為兩個由細果凍線連線在一起的甜甜圈。(或者也許我只是餓了。)
相信我,你不會想看到我嘗試用 3D 繪製這個。
有趣的是,檯球桌上的狹縫與環面上的狹縫是不同的狹縫!我在環面上用白色繪製了狹縫,以將其與球桌上的狹縫或障礙物區分開來。在這種情況下,當軌跡撞擊一個環面上的狹縫時,它會從另一個環面上的狹縫中彈出,並沿相同的方向繼續前進。再一次,狹縫就像一個蟲洞,這次是在兩個環面之間。
既然我已經不厭其煩地描述了這個空間,那麼重點是什麼?為什麼有人會喜歡沿狹縫粘合的兩個環面?我問了我的配偶,他說他喜歡它,因為它與環面或矩形中的檯球足夠不同以至於有趣,但又足夠相似,以至於用於研究環面的一些技術也適用於那裡。他還告訴我數學家可以為此設計出一些有趣的行。
動力系統中的一個基本問題是事物如何分佈。在多邊形中的檯球或曲面上的流的情況下,這意味著我們試圖弄清楚軌跡是否填滿曲面,如果填滿了,它是均勻地填滿所有曲面,還是有些部分比其他部分更密集。
有兩個性質相關但不完全相同,沿狹縫粘合的環面有助於闡明這兩個性質。第一個是密度。如果流無限次地擊中空間中的每個矩形,無論矩形有多小,則該流是密集的。第二個是均勻分佈。如果流擊中每個矩形的次數與其面積成正比,則該流是均勻分佈的。也就是說,它一半的時間在矩形的上半部分,四分之一的時間在矩形的左下四分之一部分。
對於沒有狹縫的矩形/環面,沒有非均勻分佈的密集流。在這空間中,這兩個性質是等價的。但是對於帶有障礙物的矩形,它們是不同的。根據狹縫的長度,一些軌跡可以是密集的,因此它們會擊中球桌的每個部分,但在球桌的某些部分花費的時間比其他部分更多。
當我們開始談論沿狹縫粘合在一起的兩個環面時,我不斷地問我的配偶一個又一個問題。他告訴我的越多,我有的問題就越多。有些答案是已知的,有些則不是。撇開我的繪畫技巧不談,我在這裡展示的所有狹縫都應該正好位於矩形側邊的中間,因此你得到的兩個環面,橙色的和藍色的,大小相同。我的配偶說,如果你移動狹縫,使其位於矩形側邊的 2/3 處,行為是未知的。因此,我喜歡這個空間的另一個原因是,構造並不太困難,但我可以稍微調整一下它,就能找到即使是該領域的專家也還沒有答案的問題!
閱讀更多我最喜歡的空間: 康託集 胖康託集 拓撲學家的正弦曲線 康託的漏帳篷 無限耳環 具有兩個原點的直線 帶有兩個房間的房子 法諾平面 環面 三環面 莫比烏斯帶 長線 空間填充曲線 沃利斯篩
