本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點

用鉤編制作的可愛克萊因四次曲線。圖片版權歸戴娜·泰米娜所有。經許可使用。
上週,數學家兼藝術家戴娜·泰米娜在Twitter上分享了她的最新創作。這是一個名為克萊因四次曲面的模型。它是不是很可愛?
那麼它是什麼呢?克萊因四次曲面是一個具有3個孔的二維物體,它有很多對稱性。事實上,它擁有一個具有3個孔的曲面可能擁有的最大對稱性:168個保持曲面方向的對稱性,以及168個涉及將曲面由內而外翻轉的對稱性。
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您將幫助確保未來能夠繼續講述關於塑造我們當今世界的發現和思想的具有影響力的故事。
定義克萊因四次曲線的方法有幾種,泰米娜使用了一種涉及將 24 個七邊形(7 邊形)縫合在一起的方法。它基於七邊形對雙曲平面的 tiling(密鋪)。好的,但這到底意味著什麼呢?
很容易想象用六邊形對規則的二維歐幾里得平面進行密鋪。我們經常看到這種情況,從浴室瓷磚到蜂巢。正六邊形的每個角都是 120 度,當我們把三個六邊形在一個頂點處粘合在一起時,我們得到的東西是 360 度,這非常平坦,並且恰好適合平面。

這些黃蜂喜歡用正六邊形密鋪平面!圖片來源:Shardayy,via flickr。
如果我們使用五邊形而不是六邊形,我們仍然可以將三個五邊形在一個點處粘合在一起,但我們最終得到的不是 360 度,而只有 324 度,因為正五邊形的每個角都是 108 度。我們不能用它們密鋪平面,但我們可以將它們粘合在一起,並將它們閉合成一個非常漂亮的曲面,即十二面體。
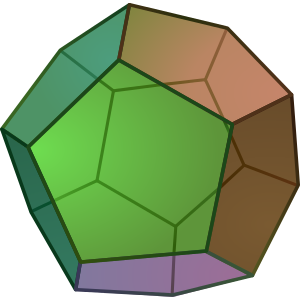
十二面體。圖片來源:DTR,via Wikimedia Commons。
另一方面,如果我們使用七邊形,我們得到的不是角度虧損,而是角度盈餘。正七邊形的每個內角略大於 128 度,所以當我們把三個七邊形在一個頂點處放在一起時,我們得到的角度大於 360 度。再一次,我們不能用它們密鋪歐幾里得平面,但我們可以密鋪一種叫做雙曲平面的東西,這是一個神奇的仙境,在那裡三角形的角度不必加起來等於 180 度,獨角獸是真實存在的。*
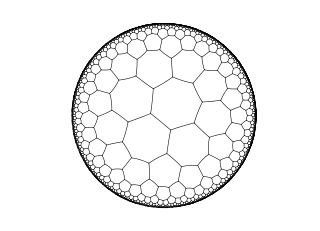
七邊形對雙曲平面的密鋪。用“雙曲眼睛”觀察,這些七邊形大小相同,邊都是完全直的。在這張圖片中,一些邊緣略微彎曲,以使它們“適合”歐幾里得平面。圖片來源:Theon,via Wikimedia Commons。
一旦你用七邊形密鋪了雙曲平面,你就可以以某種方式將其中 24 個粘合在一起,從而建立一個克萊因四次曲面,而這正是泰米娜所做的。你可以在她的部落格上閱讀更多關於她如何製作它的細節,以及從John Baez和Greg Egan那裡瞭解一些其他理解這個曲面的方法。克萊因四次曲線無法在三維空間中完全實現,因為我們無法制作一個具有所有可能對稱性的模型。曲面上的白色把手讓我們瞭解如果泰米娜和她的鉤編模型沒有和我們其餘的人一樣被困在無聊的三維歐幾里得空間中,它將如何被粘合在一起。
我一直是泰米娜作品的粉絲。據我所知,她是第一個使用鉤編來建立雙曲平面和其他雙曲曲面模型的人。我有點知道如何鉤編,並且我買了她的書《與雙曲平面的鉤編冒險》。當我最終有機會時,我認為研究她書中的一個專案將提高我的鉤編技巧和我對雙曲幾何的理解。泰米娜啟發了許多其他數學家創作雙曲空間的鉤編模型作為教學工具。我在這裡寫過其中一位。如果您對泰米娜的雙曲鉤編方法更感興趣,請檢視她的網站。
*這句話部分屬實。