本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定代表《大眾科學》的觀點
在我們最近一期的《我最喜歡的定理》節目中,我的聯合主持人凱文·努森和我與蒙特利爾大學數學教授瑪蒂爾德·拉林討論了她最喜歡的數學知識,即同餘數問題。(您可以在kpknudson.com上收聽該節目或閱讀文字記錄。)
同餘數是一個正整數,它可以是邊長為有理數的直角三角形的面積。例如,數字 6 是一個同餘數,因為它是 3-4-5 直角三角形的面積。同餘數問題是要找出哪些正整數是同餘數。
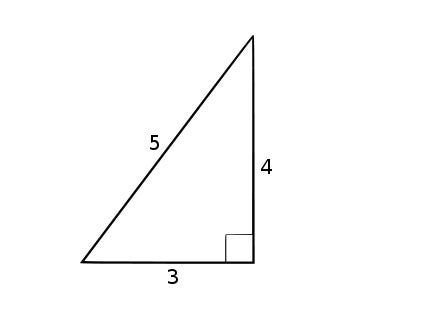
邊長為 3、4 和 5 的三角形。其面積是底乘以高的一半,即 6。圖片來源:Adrignola Wikimedia
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您將有助於確保關於當今塑造我們世界的發現和想法的具有影響力的故事的未來。
當我聽到“同餘數”這個詞時,我的第一個問題是,“與什麼同餘?”但是,即使涉及到三角形,這個名字也不是來自兩個圖形同餘的概念,而是來自拉丁語 congruum。斐波那契使用該術語,意思是“一致”或“和諧”,來指代算術級數中平方數的差。
算術級數是連續數字之間差相同的數字序列:例如,1、3、5、7 是差為 2 的算術級數。連續平方數(1、4、9、16 等)不形成算術級數,但是如果跳過一些,您可以找到一組彼此具有這種關係的平方數。平方數 1、25 和 49 的差均為 24,因此斐波那契會將 24 稱為同餘數。
我的第一個問題得到了解答,我自然而然的第二個問題:同餘數和同餘數有什麼關係?我們如何從算術級數過渡到三角形?公元 3 世紀的數學家亞歷山大城的丟番圖的作品中提到了同餘數和同餘數的早期提示,但在 10 世紀的阿拉伯手稿中,包括穆罕默德·本·阿霍欽的一份手稿中,該主題被更明確地提出,他寫道,有理直角三角形研究的主要物件是尋找同餘數。
我的第一個同餘數的例子是 6,我的第一個同餘數的例子是 24,這不是巧合。透過知道 24 是一個同餘數,我們可以構造出邊長為有理數且面積為 6 的三角形。
我們第一個例子中的同餘數是 24,算術級數中的三個平方數是 12、52 和 72。早期的數學家認識到,當三個平方數以這種方式出現在算術級數中時,中間數的平方根(在本例中為 5)就是直角三角形的斜邊。兩條直角邊的長度之和是最大數的平方根,而它們的長度之差是最小數的平方根。如果兩個數的和為 7,差為 1,一個簡單的方程組表明這兩個數是 3 和 4。那麼,三角形的面積就是 6,是同餘數 24 的四分之一。
這個想法普遍適用。任何公差為 k 的平方數序列 x2、y2、z2 都具有以下性質:k 是斜邊長度為 y,直角邊長度為 a 和 b 的直角三角形面積的 4 倍,其中 a 和 b 由兩個方程 a+b=z 和 a-b=x 確定。一下子看到所有這些似乎有點讓人不知所措,但如果您想擺弄一些符號,驗證一下並不難。
正如拉林博士告訴我們的那樣,數學家們長期以來一直在嘗試尋找確定給定數字是否是同餘數的標準。已知一些事實:沒有平方數是同餘數;如果一個素數比 8 的倍數多 3,那麼它就不是同餘數,但它的兩倍是;每個同餘數都是同餘數乘以有理數的平方。最後一個似乎像中了頭獎,但是有理數的平方有很多,而且不容易看出給定的有理數乘以同餘數是否會產生同餘數。貝赫和斯維納頓-戴爾猜想被認為是數學中最重要的未解問題之一,它的一個結果是,存在一個簡單的過程來確定給定數字是否是同餘數。
有關同餘數、同餘數和貝赫和斯維納頓-戴爾猜想的更多資訊,請檢視我們與瑪蒂爾德·拉林一起錄製的《我最喜歡的定理》節目的節目說明,或倫納德·尤金·迪克森的《數論史》第二卷。(關於同餘數的部分從連結書的第 459 頁開始。)您可以在整數序列線上百科全書中找到許多同餘數的列表。
