本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
星期一,《洋蔥報》報道稱,“國家數學教師引入 27 個新的三角函式。” 這是一篇有趣的讀物。《洋蔥報》文章中的 gamsin、negtan 和 cosvnx 是虛構的,但這篇文章有一點道理:有 10 個你從未聽說過的秘密三角函式,它們有令人愉快的名字,如“半正矢”和“正割外函式”。
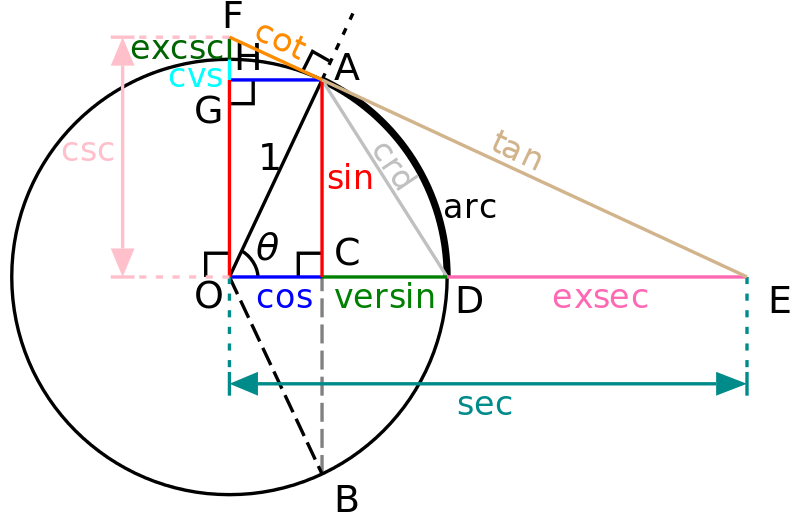
一個帶有單位圓的圖表,其三角函式多到你數不過來。(眾所周知,你最多隻能數出 8 個三角函式。) 熟悉的正弦、餘弦和正切分別用紅色、藍色和棕褐色表示。餘矢與餘弦相鄰,以綠色表示,而正割外函式在餘矢的右側,以粉紅色表示。圖中還顯示了余余割和余余矢。未顯示:余余弦、余余餘弦和半-任何東西。圖片來源:Limaner 和 Steven G. Johnson,透過 維基共享資源。
無論你是想用它們來折磨學生,還是在談話中丟擲它們來讓自己聽起來博學和/或令人討厭,這裡都是所有“丟失的三角函式”的定義
關於支援科學新聞業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞業 訂閱。 透過購買訂閱,您正在幫助確保有關塑造我們今天世界的發現和想法的具有影響力的故事的未來。
我在對原始歷史文字進行詳盡研究時發現維基百科告訴我的。
餘矢:versin(θ)=1-cos(θ)
余余弦:vercosin(θ)=1+cos(θ)
余余矢:coversin(θ)=1-sin(θ)
余余餘弦:covercosine(θ)=1+sin(θ)
半正矢:haversin(θ)=versin(θ)/2
半餘矢:havercosin(θ)=vercosin(θ)/2
半余余矢:hacoversin(θ)=coversin(θ)/2
半余余餘弦:hacovercosin(θ)=covercosin(θ)/2
正割外函式:exsec(θ)=sec(θ)-1
餘割外函式:excsc(θ)=csc(θ)-1
我必須承認,當我查閱這些函式時,我有點失望。它們都只是親愛的舊正弦和餘弦的簡單組合。它們為什麼甚至有名字?! 在一個我可以坐在沙發上,使用線上計算器幾乎瞬間找到任何角度的正弦值,精確到小數點後 100 位的地方,餘矢是不必要的。 但是,這些看似多餘的函式在沒有計算器的世界中滿足了需求。
Numberphile 最近釋出了一個關於 對數表的影片,該影片解釋了在黑暗的無計算器時代,人們如何使用對數來乘大數。 首先,複習一下對數。 方程 logbx=y 表示 by=x。 例如,102=100,所以 log10100=2。 關於對數的一個方便的事實是 logb(c×d)=logbc+logbd。 換句話說,對數使乘法變為加法。 如果你想使用對數表將兩個數字相乘,你需要查詢兩個數字的對數,然後將對數相加。 然後,你將使用你的對數表找出哪個數字具有該對數,那就是你的答案。 現在聽起來很麻煩,但是手動進行乘法運算比加法運算需要更多的操作。 當每個操作都需要相當長的時間(並且容易出現相當大的錯誤)時,一種可以將乘法轉換為加法的過程是真正的節省時間的方法,並且可以幫助提高準確性。
像對數一樣,秘密三角函式使計算更容易。 餘矢和半正矢使用最多。 在接近角度 θ=0 時,cos(θ) 非常接近 1。 如果你在進行包含 1-cos(θ) 的計算,如果你的餘弦表沒有足夠的有效數字,你的計算可能會被破壞。 為了說明這一點,5 度的餘弦為 0.996194698,1 度的餘弦為 0.999847695。 差值 cos(1°)-cos(5°) 為 0.003652997。 如果你的餘弦表中有三個有效數字,由於差值中的前導零,你只能在答案中獲得 1 位有效數字的精度。 精度僅為三位有效數字的表格將無法區分 0 度角和 1 度角。 在許多情況下,這無關緊要,但如果誤差在計算過程中累積,則可能會成為問題。
獎勵三角函式也具有永不為負的優點。 餘矢的範圍在 0 到 2 之間,因此如果你使用對數表與餘矢相乘,你無需擔心對數未針對負數定義的事實。 (它也沒有為 0 定義,但這很容易處理。) 餘矢和半正矢的另一個優點是它們可以讓你不必平方。 一點三角魔法(又名,記住你在高中學到的無窮無盡的三角公式之一)表明 1-cos(θ)=2sin2(θ/2)。 所以半正矢只是 sin2(θ/2)。 同樣,半餘矢是 cos2(θ/2)。 如果你的計算涉及正弦或餘弦的平方,你可以使用半正矢或半餘矢表,而無需平方或開平方根。
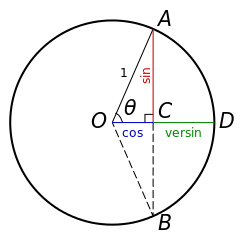
一個顯示角度的正弦、餘弦和餘矢的圖表。 圖片來源:Qef 和 Steven G. Johnson,透過 維基共享資源。
餘矢是一個相當明顯的三角函式,定義似乎可以追溯到公元 400 年的印度。 但是,半正矢在近代歷史上可能更為重要,當時它被用於導航。半正矢公式是一種非常準確的計算球體表面上兩點之間距離的方法,使用兩點的緯度和經度。 半正矢公式是球面餘弦定律的重新表述,但是用半正矢的公式對於小角度和距離更有效。(另一方面,半正矢公式對於接近 90 度的角度效果不佳,但球面餘弦定律可以很好地處理這些角度。) 半正矢公式可以產生準確的結果,而無需進行計算量大的平方和平方根運算。 早在 1984 年,《天空與望遠鏡》業餘天文學雜誌還在讚揚半正矢公式,該公式不僅對陸地導航有用,而且對天體計算也很有用。 有關半正矢公式和計算球體上距離的更多資訊,請檢視此人口普查局頁面的存檔副本或此Ask Dr. Math文章。
我沒有關於列表中其他三角函式的歷史的太多資訊。 所有這些函式都可以使某些角度附近的計算更準確,但我不知道哪些函式常用,哪些函式是*與其他函式類似地命名但很少實際使用。 我對此感到好奇,如果有人對該主題了解更多,請告訴我!
當《洋蔥報》模仿現實生活時,通常是悲劇。 但是在秘密三角函式的情況下,《洋蔥報》中的一點道理並沒有讓我感到難過。 我們現在非常幸運,我們可以如此輕鬆地進行乘法、平方和開平方根運算,並且我們的計算器可以儲存關於角度的正弦、餘弦和正切的精確資訊,但是在我們能夠做到這一點之前,我們以荒謬數量的三角函式的形式找到了一個變通方法。 很容易忘記定義它們的人不是虐待狂的數學老師,他們希望人們記住奇怪的函式,沒有任何理由。 這些函式實際上使計算更快,更不容易出錯。 現在計算機如此強大,半正矢已經像軟盤一樣過時了。 但我認為我們都可以同意它應該回歸,即使只是為了我昨晚睡著時想出的“真棒”笑話:半正矢? 我甚至不認識她!
*我想在這裡稍微跑題到數學字首的世界,但這可能不適合所有人。 已警告你。
在秘密三角函式表中,“半”顯然意味著一半; 例如,半正矢的值是餘矢值的一半。“餘”意味著取相同的函式,但使用餘角。 (餘角加起來為 90 度。在直角三角形中,兩個非直角是互餘角。) 例如,一個角的餘弦也是其餘角的正弦。 同樣,余余矢是餘角的餘矢,正如你在帖子頂部的圖表中紅色正弦之一上方的淺藍色中看到的那樣。
讓我有點困惑的一個獎勵三角函式是余余弦。 如果該定義中的“餘”表示餘角,那麼余余弦將與余余矢相同,但事實並非如此。 相反,余余弦是補角(補角加起來為 180 度)的餘矢,而不是餘角的餘矢。 除了定義為 1-cos(θ) 和 1+cos(θ) 之外,餘矢和余余弦也可以定義為 versin(θ)=2sin2(θ/2) 和 vercos(θ)=2cos2(θ/2)。 就餘矢而言,我相信涉及 cos(θ) 的定義比涉及正弦平方的定義更古老。 我猜余余弦是一個後來的術語,是使用餘弦代替正弦平方定義的餘矢的類比。 如果你是三角學歷史愛好者,並且有更多資訊,請告訴我! 無論如何,超級秘密獎勵三角函式表是一個有趣的練習,可以弄清楚字首的含義。