本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
我見過的最巧妙的紙牌魔術不是由魔術師表演的,而是一位數學教授表演的。
一位助教(我們稱他為尼克),充當魔術師的助手,招募了五名學生參與者。每個學生從一副 52 張的紙牌中選一張,然後面朝上但湯姆教授看不到地交還給尼克。尼克將這四張牌放在湯姆面前。令我們驚訝的是,湯姆立即認出了缺少的第五張牌。
教授在課結束時揭示了訣竅。但是當我興奮地回到宿舍時,我的室友本傑明拒絕讓我解釋它;他必須自己弄清楚。他喃喃自語地走回自己的房間,幸福地沒有意識到在 24 小時內,這個謎題將證明對他的尊嚴是災難性的。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞工作 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
紙牌魔術通常依賴於欺騙或手法,但這一個完全是關於數學的。理論上,這是大學水平的數學,但它歸結為我們所有人五歲時都學到的東西:計數。
雖然這個魔術旨在突出魔術師,但稍微數一下就會發現助手才是真正的明星。畢竟,尼克不僅僅是一個紙牌管家,而是一個合作者:他可以選擇四張牌的順序,向湯姆傳達資訊。不僅如此,他還可以選擇展示五張牌中的哪四張。因此,讓我們計算一下可能性:有五種方法可以選擇一張秘密卡;然後,他展示的第一張牌有四個剩餘的選擇,下一張牌有三個選擇,依此類推。這給了尼克任何五張牌的 5 x 4 x 3 x 2 x 1 = 120 種選擇。

圖片來源:傑西·杜尼茨
因此,艱苦的工作在於尼克,他必須戰略性地選擇這 120 個選項之一;湯姆只需解釋他所展示的內容。這種協作安排比讀心術容易得多,但說起來容易做起來難。根據“簿記員規則”(計數原則都有很好的名字),有 260 萬種可能的五張牌組合。不知何故,尼克必須能夠瞥一眼這些牌中的任何一張,並挑選四張牌向湯姆傳送一條編碼資訊,告訴他第五張牌的花色和點數。尼克如何讓紙牌說話?
在看過魔術後的晚上,我和一個同學在做我們的計數作業(是的,真的),這時本傑明出現在廚房裡。他用他標誌性的動畫風格,喋喋不休地說他已經弄清楚尼克可以選擇展示哪些牌,甚至為尼克設計了一個與湯姆交流的系統。“但我還沒有完全弄清楚——我還有一個資訊無法弄清楚如何編碼!”
當我們交談時,本傑明靠在牆上,牆上有一個大的方形垃圾桶。他逐漸沿著牆下滑,直到他放在背後的雙手抓住垃圾桶的邊緣。
本傑明弄清楚的是一個核心的計數原則,稱為鴿籠原理。(告訴過你它們的名字很好聽。)想象一個有九個鴿籠的鴿舍。如果有十隻鴿子試圖在裡面休息,那麼至少有一個籠子裡有不止一隻鴿子是數學上的必然。

十隻鴿子太多了——肯定有一個鴿籠裡有兩隻鴿子! 圖片來源: 維基百科(CC BY-SA 3.0)
雖然看似顯而易見,但鴿籠原理導致許多非顯而易見的結論。例如,我們知道有四種花色的紙牌。不可避免的是,當湯姆的觀眾抽出五張牌時,其中兩張必須是同一花色。

應用於撲克牌花色的鴿籠原理:花色是鴿籠,紙牌是鴿子。只有四種花色,因此即使四張牌的花色不同,第五張牌也必須與其中一張花色相同。圖片來源:傑西·杜尼茨
應用於撲克牌花色的鴿籠原理:花色是鴿籠,紙牌是鴿子。只有四種花色,因此即使四張牌的花色不同,第五張牌也必須與其中一張花色相同。
這表明尼克可以輕鬆地傳達隱藏牌的花色。假設五張牌包括 J♡ 和 K♡。尼克可以將 J♡ 作為隱藏牌,並將 K♡ 作為四張牌程式碼中的第一張,告訴湯姆秘密牌也是紅桃。
但仍然缺少一個關鍵部分。一旦尼克拿出第一張牌,他就只剩下三張牌了。有六種排列三張牌的方法——但湯姆必須在花色中的所有十三張牌之間做出選擇。根據相同的鴿籠原理,六種紙牌排列方式無法唯一地編碼十三種可能性;某些排列方式必須是模稜兩可的!如何將點數也塞入展示的紙牌中?
本傑明已經弄清楚了這一切。他甚至有一個基於計數的證明,證明尼克可以將他的資訊有效載荷增加一倍:由於至少有兩張牌花色相同,尼克可以選擇展示哪一張。這給了他兩倍的選擇,對於第一張牌的每種可能選擇,有六個選擇。
但這仍然只有尼克可以傳送的十二條可能的訊息。但實際上,十二個剛剛好——尼克選擇的花色中的一張牌將在湯姆面前面朝上!這讓湯姆的猜測只有十二種可能性。尼克擁有足夠的資訊攜帶能力。
但是在這裡,本傑明卡住了。說必須能夠傳達必要的資訊是一回事;做到這一點是另一回事。本傑明只是無法弄清楚如何將這些見解轉化為實際程式碼。
為了使這項工作起作用,我們需要一個圓圈——特別是這一個
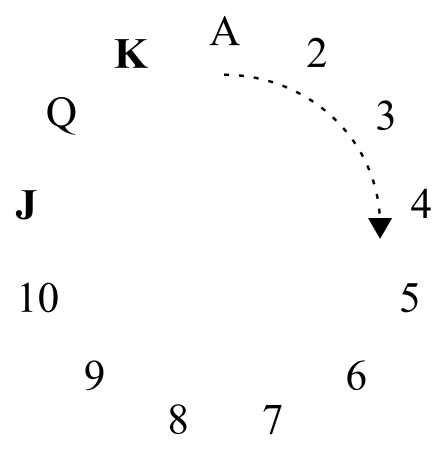
圖片來源:傑西·杜尼茨
這個圓圈的有趣之處在於,尼克始終可以確保隱藏的牌與第一張顯示的牌最多相差順時針六步。假設牌組由下面顯示的五張牌組成(J♡、Q♧、9♢、Q♤ 和 K♡)。尼克必須選擇先顯示 J♡ 或 K♡。如果他選擇 K♡,那麼 J♡ 在圓上順時針跳躍 11 步。但是,如果他顯示 J♡,那麼只需兩步即可到達 K♡!透過戰略性的選擇,尼克可以給魔術師一個起始點,使真實值僅在順時針方向的幾步之內。
五張牌的示例。助手應該向魔術師展示前四張,告訴他最後一張是 K♡。© Chris Aguilar,LGPL 3.0。

五張牌的示例。助手應該向魔術師展示前四張,告訴他最後一張是 K♡。圖片來源:Chris Aguilar LGPL 3.0
剩下的就是讓尼克告訴湯姆 1 到 6 之間的跳躍次數。他們透過預先商定牌組中所有紙牌的順序來實現這一點。一種明智的選擇是借鑑橋牌,其中花色按梅花、方塊、紅桃和黑桃(從低到高)排序,並且同一花色中的點數按二到 A 的順序排序。在我們的示例中,9♢ 將“大於”Q♧,但小於 Q♤。使用此順序,尼克和湯姆建立了一個程式碼,將紙牌序列轉換為數字:小/中/大表示 1,小/大/中表示 2,依此類推。
接下來是用於將紙牌序列轉換為圓上步數的完整表格。請訪問此互動式頁面,嘗試親自解碼助手的訊息。
紙牌順序 | 含義 |
小、中、大 | 1 |
小、大、中 | 2 |
中、小、大 | 3 |
中、大、小 | 4 |
大、小、中 | 5 |
大、中、小 | 6 |
在我們的示例中,尼克將向魔術師展示上面顯示的前四張牌(J♡、Q♧、Q♤ 和 9♢)。第一張牌告訴湯姆秘密花色是紅桃。因為剩餘的紙牌按小/大/中的順序排列,所以他知道秘密值是 J♡ 順時針方向的兩步。僅憑這四張牌,湯姆就可以正確猜出 K♡。
可悲的是,本傑明從未達到圓圈魔術的程度。當他懸在垃圾桶上方時,他突然受到啟發,然後大喊一聲“哦!”並舉起了雙臂。
他忽略考慮的是,他所有的重量都壓在了那雙胳膊上。瞬間,他的身體塌陷到垃圾桶裡,胳膊和腿像倒立的烏龜一樣搖擺。他來回搖晃,但無濟於事:他被困住了。
當然,我的第一反應是歇斯底里地大笑並拍了一張照片。
本傑明被困在垃圾桶裡時表現得很好。他發誓說他沒有穿褲子。圖片來源:傑西·杜尼茨
我趕緊衝過去想幫他一把,但我喘得太厲害了,結果只是把自己弄得摔倒在地,在地上打滾大笑。最後,我那個不那麼沒用的作業夥伴出手了。她把那可憐的人類烏龜翻了過來,並把罐子從本傑明的屁股上拔了下來,讓他得以溜走舔舐傷口。
在數學中,計數能讓你走得相當遠。你只需要它就可以弄清楚倫敦是否有兩個人頭上的頭髮數量相同(確實有),或者在撲克牌中拿到葫蘆的機率。並且冒著聽起來像伯爵的風險,這種計數不僅可以提供資訊,而且令人愉快(啊-哈-哈-哈!)。
自從我上完那門課後,講師們顯然已經從講座中刪除了這個演示。毫無疑問,他們聽說了他們的數學遊戲給大學其他地方帶來的危險。我想你必須小心計數。如果你不小心,它真的會咬你的屁股。
