本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定代表《大眾科學》的觀點
大眾科學和數學作家馬丁·加德納(1914-2010)被認為創作了 101 本非小說類書籍和一些小說,他本應在 10 月 21 日迎來 101 歲生日。在馬丁在《大眾科學》的 數學遊戲 專欄中 25 年期間提出的無數數學問題中,有相當多的問題引發的問題多於答案,這實際上是一件好事。
數學遊戲 品牌的影響力以及對娛樂數學重要性的認可在今天仍然存在,馬丁的讀者現在跨越了幾代人。他的鐵桿粉絲繼續每兩年在亞特蘭大舉辦僅限邀請的“加德納聚會”,任何人(任何地方)都可以在每年 10 月左右參加或主辦頭腦慶典。最重要的是,人們不斷透過為他的難題提供實質性的新解決方案以及對舊情節的新轉折來推動極限。
下面,我們回顧一下一些直觀的二維解剖和鑲嵌突破,這些突破最初讓馬丁的讀者感到興奮。令人高興的是,一些結果是最近才出現的,證實了馬丁的信念,即娛樂數學除了能為好奇心和創新提供自然的跳板外,還能導致真正的持續研究。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞工作 訂閱。透過購買訂閱,您正在幫助確保未來關於塑造我們當今世界的發現和想法的具有影響力的故事。
三角形和正方形
解剖涉及將熟悉的形狀分解成有限數量的有趣的小塊,而鑲嵌則涉及用一些特定形狀或形狀的副本填充無限空間的雙重概念。
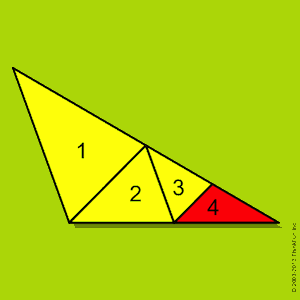
這是馬丁在他 1960 年 2 月的專欄中提出的一個簡單的解剖問題:“給定一個有一個鈍角的三角形,是否可以將三角形切割成較小的三角形,所有三角形都是銳角的?”當然,最初的嘗試,例如右圖所示的嘗試失敗了(小三角形 4 不是銳角)。
這是他在 1981 年 4 月專欄中提出的一個更難的問題:“一個正方形可以分成最少多少個不重疊的銳角三角形?”令人驚訝的解決方案是他的原創。另一個來自 1989 年的難題至今仍未解決,歸功於理查德·蓋伊,他剛剛在飛往阿西尼博因山頂的直升機之旅中慶祝了他的 99 歲生日,他問是否可以用整數邊長對正方形進行三角剖分,使得生成的三角形也具有整數邊長?正如理查德本月在電子郵件中所說,我們仍然不知道是否可以在單位正方形的平面中找到一個到四個頂點的距離為有理數的點。
在 1958 年 11 月,馬丁問一個正方形是否可以被解剖成有限數量的邊長不同(整數)的小正方形,避免出現矩形子集——棋盤圖案之類的在這裡沒有意義。自 20 世紀 30 年代以來,人們就知道這與電力網路理論有關。馬丁提供的近似解決方案——一個被解剖成正方形的 32x33 矩形——那個月登上了雜誌的封面(十幾個此類封面中的第一個)。
找到合適的“平方數”解決方案花了 20 年時間,其中一個是邊長為 112 個單位的正方形,它按要求細分為 21 個正方形。馬丁給出的關於為什麼沿這些方向在三維空間中不起作用的令人信服的基本論證——這意味著一個立方體不能被分解成有限數量的不相等的立方體——自從 40 年前第一次閱讀它以來就一直困擾著我。由此可見,它在任何更高的維度上也行不通!
現在,讓我們透過切換到鑲嵌,從字面上跳出正方形的框框。在 1979 年 10 月,馬丁寫到了他的老朋友索爾·戈隆布在 1975 年提出的挑戰:整個無限平面可以用正方形進行鑲嵌嗎,每個整數邊長一個(1、2、3、4...)?
戈隆布的挑戰一直沒有被攻克,直到 吉姆·亨利和他的兒子弗雷德在 2008 年征服了它。吉姆解釋說:“證明的關鍵是一個引理,它指出給定任何 L 形區域,都可以新增正方形來形成一個矩形。下面的動畫展示了當從一個由 28x28 正方形和一個 17x17 正方形形成的 L 形開始時,這是如何完成的。”(為了便於視覺化,正方形被顯示為擴充套件到 3D 立方體。)
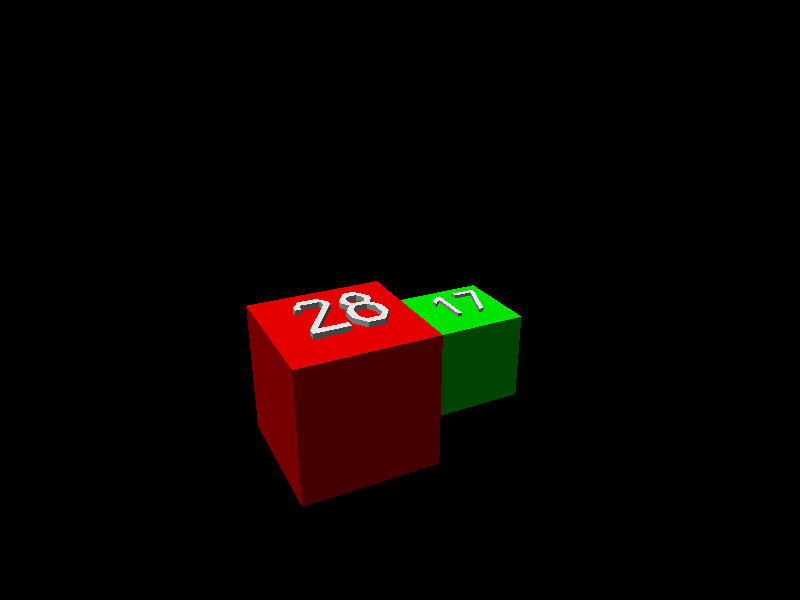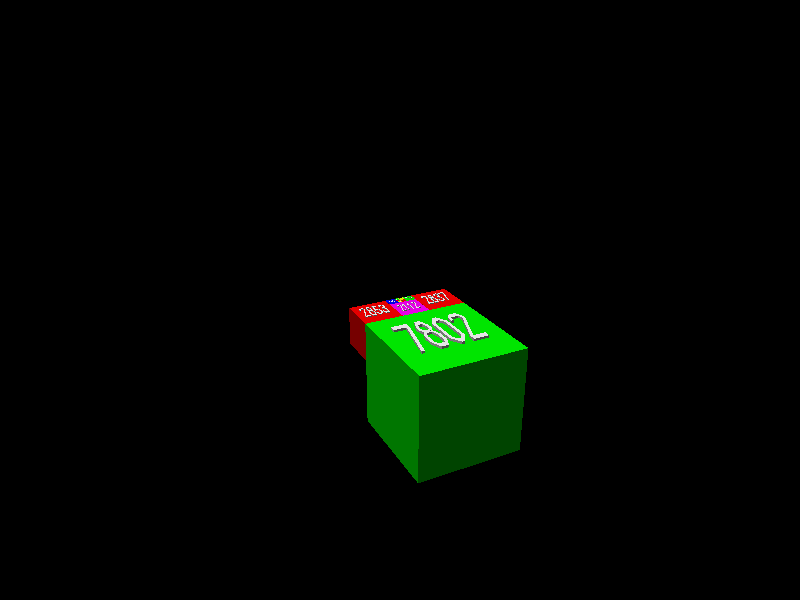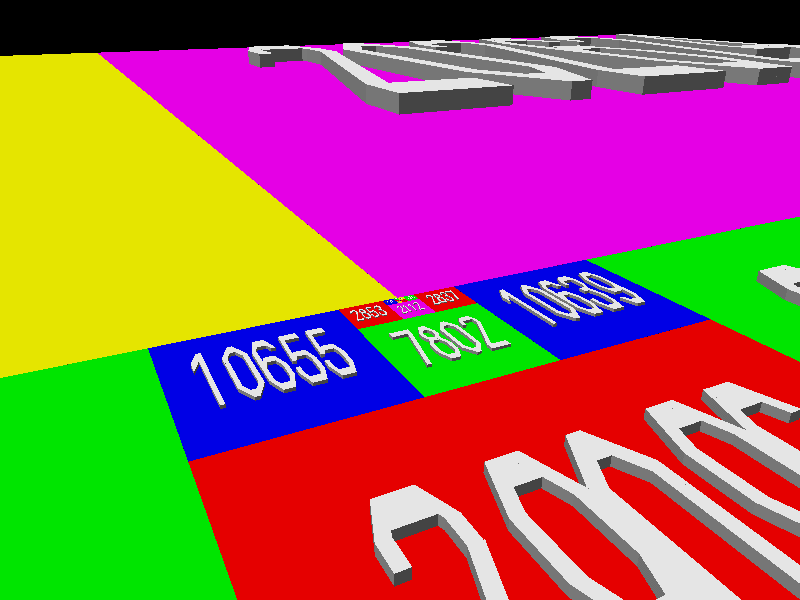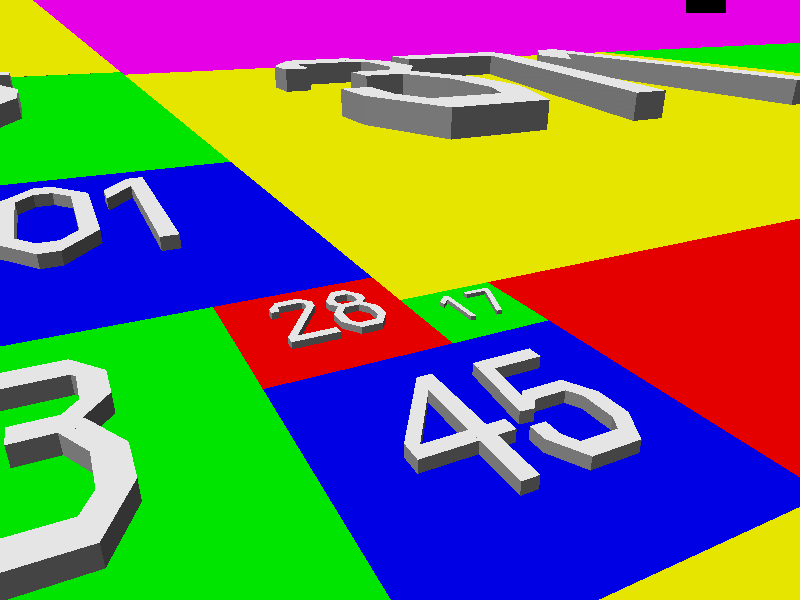
由吉姆·亨利提供。
亨利繼續說道:“證明很容易從引理得出,因為一旦形成一個矩形,你可以取尚未在鑲嵌中的最小正方形,並將其新增到矩形中,形成另一個 L 形(然後可以用更多的正方形擴大它,形成另一個矩形,依此類推)。”因此,每個可能的整數邊長的正方形都將被生成,因為缺失的正方形將被計算在內,並且平面(在立方體之上)將被完全鑲嵌。
在他們的論文末尾,作者討論了使用三角形在類似約束條件下鑲嵌平面的可能性,並提到了另一個仍然未解決的問題:“是否可以用所有有理等邊三角形鑲嵌平面,使得沒有三角形有無限個鄰居?”
在另一個狡猾的腦筋急轉彎中,馬丁展示了將一個三鑽解剖成四個全等凸塊,並要求使用五個全等凸塊解剖一個正方形。
事後看來,答案是顯而易見的——我們有沒有提到馬丁也是一位王牌魔術師,因此也是一位誤導大師?然而,直到上個月(在 Liping Yuan、Carol Zamfirescu 和 Tudor Zamfirescu 的預印本“將正方形分解為五個全等的部分”中)才宣佈了證明不存在其他解決方案的證明。
永遠令人驚訝的五邊形
超越三邊形和四邊形,我們來到了五邊形,即五邊形。 正則凸五邊形不能獨自鑲嵌平面,因為完全對稱的三角形、正方形和六邊形可以,但不規則的五邊形可以做到。 下面顯示的各種可能性都可以在互動式Wolfram 五邊形鑲嵌演示專案網站上進行探索。 這個故事始於一個世紀前,當時卡爾·萊因哈特發現了五種不同型別的五邊形鑲嵌。 以下是其中的兩個

左圖:第 1 類五邊形鑲嵌(Tomruen/Wikimedia)。右圖:第 2 類五邊形鑲嵌(Tomruen/Wikimedia)
五十年後,在 1968 年,理查德·克什納發現了另外三種類型,在馬丁於 1975 年 7 月的專欄中對此進行了報道後,理查德·E·詹姆斯發現了另一種型別。馬丁在隨後的專欄中如實地報道了這一點,聖地亞哥的中年家庭主婦瑪喬麗·賴斯在她兒子的雜誌副本中讀到了這篇文章。儘管沒有接受過數學訓練,但她開始探索和整理自己的想法,並創造了自己的符號來跟蹤她的發現。到 1977 年,她發現了其他人之前錯過的四種全新的平面五邊形鑲嵌型別,從而震驚了數學界,其中兩種如下所示
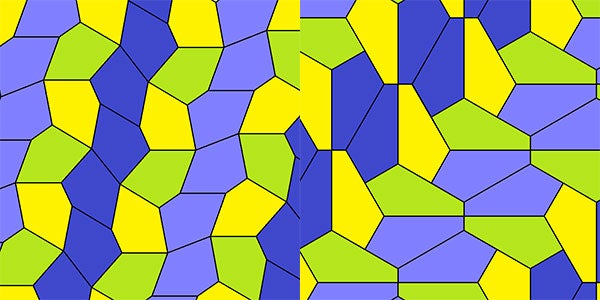
左圖:第 9 類五邊形鑲嵌(Tomruen/Wikimedia)。右圖:第 13 類五邊形鑲嵌(Tomruen/Wikimedia)
她的一個鑲嵌——在 1995 年發現——被用作美國數學協會華盛頓特區總部的地板鑲嵌,由數學家多麗絲·沙茨施耐德改編。

1985 年,羅爾夫·斯坦發現了另一種五邊形鑲嵌型別,使總數達到 14 種。三十年過去了,凱西·曼、詹妮弗·麥克勞德和大衛·馮·德勞都在華盛頓大學博塞爾分校於去年 7 月宣佈了第 15th 種類型。以下是它的一個化身

第 15 類五邊形鑲嵌。(Tomruen/Wikimedia)
為了便於比較,以下是博塞爾團隊提供的新面板中的所有 15 種鑲嵌型別

點選放大。
是否還有其他型別的五邊形鑲嵌尚未被發現?如果有,可能會有多少種?詹妮弗·麥克勞德是一位美國原住民,也是她家中第一個獲得學士學位的人,她指出,“關於用凸五邊形鑲嵌平面的方式的數量,沒有已知的上限。”換句話說,可能還有數十種五邊形鑲嵌型別——甚至無限多種。或者也許不再有任何型別。
釘上棺材
仔細觀察博塞爾五邊形是很有啟發意義的,它類似於一個不規則的棺材。也許麥克勞德和同事們真的已經透過發現最後一種可能的五邊形鑲嵌型別而釘上了棺材!
由華盛頓大學博塞爾分校提供
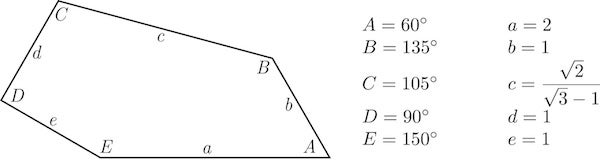
請允許我們(咳咳)研究以下角度:此形狀可以透過以下方式獲得:首先是一個鉸接的水平 5 單位長的直棒 CDEaAB,[此處“a”是指影像中 EA 段的中點;它也指 EA 的長度],然後進行如下調整。
在右側,將 AB 逆時針旋轉 120 度,使角 A 為 60 度。在左側,將 CD 順時針旋轉到垂直位置,然後保持角 D 為 90 度,再將 DE 順時針旋轉 30 度。 EaA 保持直線,長度為 2 個單位。最後連線端點 D 和 B:事實證明,DB 的長度為 sqrt(2)/(sqrt(3)-1),約為 1.93 個單位,角 C 和 B 分別正好為 105 度和 135 度。五邊形可以分解為一個等腰三角形、一個等邊三角形和一個具有“好”角的四邊形。
一個孩子隨意玩弄一根吸管,在幾個關鍵位置彎曲,並且間隔適當,很容易就能得到這種五邊形形狀。也許,隨著時間的推移,有幾個人這樣做過。如果是這樣,他們都沒有意識到自己發現的意義,一聽到開飯的宣佈,就把它扔到一邊不再想了。誰又能說,沒有哪個孩子把吸管彎成其他可以鋪滿無限平面的新型五邊形呢?這是一種大人也可以參與的兒童遊戲。
馬丁最近出版的遺作絕對是適合兒童閱讀的,同時也帶有成年人的意味。 《註釋版愛麗絲夢遊仙境:150週年豪華版》 (W.W Norton出版) 是他暢銷書的最終更新版本,其中包含了馬丁五年前去世時留下的額外註釋。