本文發表於《大眾科學》的前部落格網路,僅反映作者的觀點,不一定反映《大眾科學》的觀點
數學家以我的名字命名了一個數學物件。它被稱為霍根曲面,或者,另一種說法,霍根非曲面。這個術語本意是侮辱,但我仍然感到榮幸。這是背景故事,它也關於數學領域的變革,這是所有尋求真理的努力中最純粹的領域。
1993年,當我還是《大眾科學》雜誌的全職撰稿人時(不像我現在這樣只是一個簡陋的博主),我的老闆命令我寫一篇關於數學的深度報道。我抵制這項任務。在大學裡,我主修英語。我只上過一門數學課,是微積分。我可以處理關於剛剛被解決的費馬最後定理,或者曼德勃羅集的簡短新聞報道,但一篇主要的文章會太難。我的老闆堅持要我寫。
我開始閱讀書籍和文章,並採訪著名的數學家,最終我意識到我有一個故事。一個大故事。幾千年來,證明一直是數學真理——以及一般知識——的黃金標準。有什麼比勾股定理更真實的呢?但是數學正在以削弱傳統證明地位的方式發生變化。
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道: 訂閱。透過購買訂閱,您正在幫助確保未來能夠繼續講述關於塑造我們當今世界的發現和想法的有影響力的故事。
一個問題是數學日益增長的複雜性和專業化,這使得某些所謂的證明難以驗證。安德魯·懷爾斯對費馬最後定理的證明就是一個例子。當這份長達200頁的密集證明首次出現時,只有少數專家有資格對其進行評估。(結果證明它有一個錯誤,懷爾斯最終糾正了。)
與此同時,資助機構正在向數學家施壓,要求他們從事密碼學和人工智慧視覺等應用領域的研究。在應用數學中,動機問題從“它是真的嗎?”轉變為“它有效嗎?”數學不再是啟迪和美的源泉,不再為了自身而實踐,而變成了一種工具,一種達到實際目的的手段。
數學家們越來越依賴計算機來進行艱苦的計算、模擬物體和執行實驗。一些人主張接受所謂的機率證明,這種證明只有一定的可能性為真。另一些人則敦促證明應以計算機可以檢查而不是容易犯錯的人類可以檢查的形式書寫。
傳統主義者對這些趨勢感到痛惜,他們斷言,依賴計算機的證明根本不是真正的證明。但有影響力的人物支援這些變革。其中一位是威廉·瑟斯頓,他於1982年因闡明拓撲學和幾何學之間的聯絡而榮獲菲爾茲獎——數學界的諾貝爾獎。
瑟斯頓是我文章的主要資訊來源,他提倡更自由、更“直觀”的數學研究、交流和教育風格,減少對傳統證明的強調。他試圖用計算機生成的模型來傳達數學概念,包括他稱之為“非結”的影片。
瑟斯頓告訴我,“數學原則上可以簡化為形式證明,這種想法是不牢靠的”,這是20世紀特有的。具有諷刺意味的是,他指出,伯特蘭·羅素和庫爾特·哥德爾在本世紀初就證明了數學充滿了邏輯矛盾。“集合論是建立在客氣的謊言之上的,即使我們知道它們不是真的,我們也同意這些謊言,”瑟斯頓說。“在某些方面,數學的基礎具有不真實的氣息。”
“證明之死”以“非結”的劇照為插圖,是1993年10月《大眾科學》的封面故事。副標題是:“計算機正在改變數學家發現、證明和交流思想的方式,但在這個勇敢的新世界中,絕對的確定性還有立足之地嗎?”
我的引言中寫道:幾千年來,數學家們一直根據他們可以透過證明——即從一組公理到無可辯駁的結論的一系列邏輯步驟——來證明的東西來衡量進步。現在,困擾現代人類思想的懷疑終於感染了數學。數學家們可能最終不得不接受許多科學家和哲學家已經承認的事實:他們的斷言充其量只是暫時正確的,在被證明是錯誤之前才是正確的。
反彈——主要是以信件的形式,因為部落格那時還沒有發明——像我職業生涯中的任何一次一樣強烈。數學家們指責我歪曲事實和誇大其詞,尤其是在我選擇的標題和封面藝術上。儘管我引用了對計算機生成證據和其他趨勢的批評者的觀點,但許多數學家似乎認為我是在提倡——甚至發明——這些對傳統證明的挑戰,而不是僅僅報道它們。
一位強烈的批評者是大衛·霍夫曼,他曾是我的文章的資訊來源。霍夫曼使用計算機模型來探索極小曲面,極小曲面是由給定曲線或膜邊界的儘可能小的面積或體積。我的文章包括一張霍夫曼的照片和他用計算機生成的影像。“透過在計算機上檢視這些曲面的影像,我們獲得了大量的直覺,”霍夫曼告訴我。我還引用了他的話,他堅持認為證明仍然是研究的最終目標。
在給編輯的信中,霍夫曼寫道:“約翰·霍根的《證明之死》為了爭議和聳人聽聞而蔑視邏輯和準確性……我非常贊成在數學研究和交流中使用計算機圖形,但是,有哪位受人尊敬的數學家願意解釋和捍衛影片證明作為傳統數學方法的替代品的概念嗎?”
1998年,當霍夫曼為美國數學學會通告評論我的第一本書《科學的終結》時,仍然怒不可遏。霍夫曼並非不合理地認為“證明之死”是《科學的終結》的熱身。正如他所說,我那篇“十頁紙的數學——我們所知的數學——已經結束的文章僅僅是對科學的全面安魂曲的一次手指練習。”
霍夫曼對《科學的終結》如此受關注感到震驚。他指責我“對數學思維有明顯的反感,並且從根本上誤解了數學在科學中的用途。”他用七頁書評中的一大塊來捍衛弦理論,反對我對弦理論的攻擊。他暗示,歐洲核子研究中心的大型強子對撞機可能很快就會產生弦理論的證據——不用說,這並沒有發生。
霍夫曼把我比作19世紀神話般的專利專員,他因為一切都被髮明出來而辭去了工作。他寫道:“在21世紀末撰寫、思考和從事科學和數學的人們,將不必挖掘專利專員的半真半假的故事,來指出他們的後現代批評家的目光短淺。他們將有霍根的《終結》來發洩。”我當然希望如此。
.jpg?w=712)
圖片來源:馬蒂亞斯·韋伯
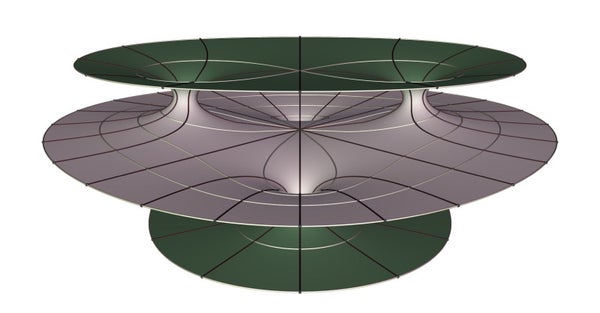
與此同時,霍夫曼繼續研究極小曲面。在“證明之死”發表後不久,他和赫爾曼·卡徹探索了一種新型曲面的變體。計算機建模最初表明,該物件是一個真正的極小曲面,但進一步調查似乎揭示了間隙(見上圖)。霍夫曼和卡徹將該物件命名為“霍根曲面”,因為他們認為這是對計算機模型可以取代嚴格證明的觀點的反駁。他們在論文《有限總曲率的完整嵌入極小曲面》中討論了霍根曲面。預印本於1995年發表,1997年,該論文被收錄在《數學科學百科全書》第5卷中。
我從數學家馬蒂亞斯·韋伯的文章中拼湊出了這段歷史,這是我最近在進行自我谷歌搜尋時發現的。1998年,韋伯在《變分法與偏微分方程》雜誌上發表了一篇論文《關於霍根極小非曲面》。韋伯指出,霍夫曼和卡徹創造了“霍根曲面”這個詞,作為對“證明之死”的“小小報復”。韋伯補充說,其他數學家“感到好笑,但要求提供一個不存在性證明。”
我想指出這裡的一個諷刺之處。霍夫曼和卡徹對我不尊重證明感到惱火,但他們並沒有為他們的猜想——霍根曲面實際上是一個偽曲面——提供任何證明!韋伯提供了證明。在他的論文中,他提出了“最對稱霍根曲面(或非曲面,他更喜歡這樣稱呼)的一個非常簡單的不存在性證明。”
最近,韋伯在兩篇部落格文章(這裡和這裡)中描述了霍根非曲面並展示了它的影像。韋伯稱這種非曲面為“一個簡單、非平凡的例子”,它是一個表面上是極小曲面,但結果並非如此的例子。“非平凡”讓我感到莫名其妙的自豪。
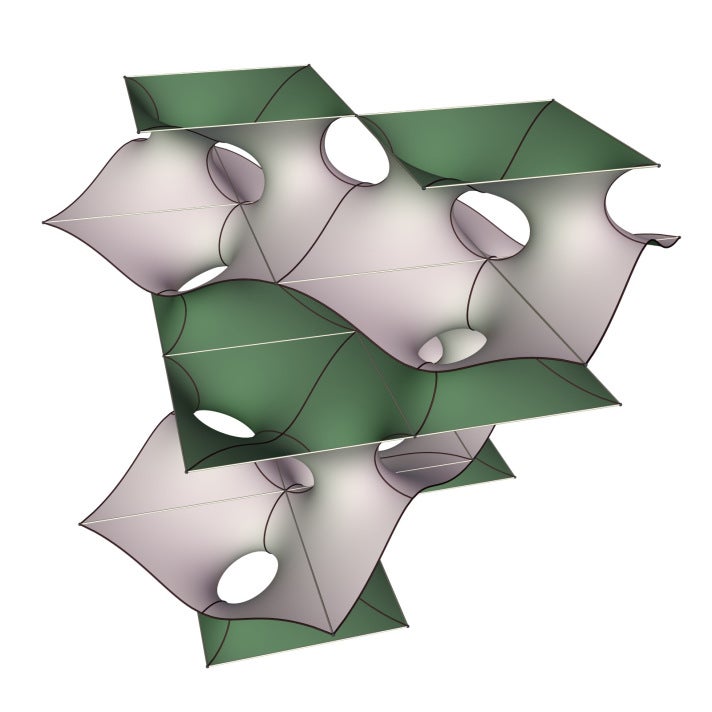
圖片來源:馬蒂亞斯·韋伯
韋伯已經證明了存在一個真正的極小曲面——“三重週期霍根曲面”(見上圖),這也讓我感到自豪。“這是霍根曲面意義重大的另一個原因,”韋伯告訴我。“這個曲面處於存在與不存在的邊緣(或者說是半死不活,如果你願意的話……),規則的細微變化就會使它倒向一邊或另一邊。”
在“沒有對稱性的嵌入極小曲面”(《微分幾何雜誌》,2002年)中,在Wolfram演示專案和我的維基百科頁面上,也可以找到關於霍根曲面的提及。我的頁面的貢獻者,可能是懷有敵意的數學家,總是對“證明之死”給予過度的關注。最近有人添加了對霍根曲面的引用,強調這個名稱是“諷刺性的”。
我後悔寫了“證明之死”嗎?當然不,就像我不後悔寫《科學的終結》一樣,《科學的終結》仍然引發爭議。我很高興在永恆的柏拉圖式形式領域中有東西以我的名字命名,即使只是諷刺性的。我更欣慰的是,數學家們繼續引用“證明之死”,即使只是為了抨擊它。我的一位最激烈的批評者史蒂文·克蘭茨在他的2011年出版的著作《證明就在布丁裡》中指出,我的文章的主要觀點“非常值得考慮”。謝謝你的讚美,史蒂夫。
韋伯在“證明之死”發表時是一名博士後,他說他“很想看到”“證明之死重灌上陣”。他詳細闡述道,“理想情況下,你應該和大衛·霍夫曼坐在一起,談談當時發生了什麼,以及今天的證明、真理、新聞業和數學是什麼樣的,然後發表出來,不加審查。” 我給霍夫曼發郵件,問他是否願意和我一起做一個問答,並承諾我會逐字逐句地刊登他的回答。霍根曲面的共同發現者“恭敬地”拒絕了。
數學界仍在為所謂的證明爭論不休——例如,黎曼猜想和ABC猜想。韋伯認為,計算機,尤其是人工智慧的進步,對傳統數學構成的挑戰甚至比1993年更大。“人們很容易想象專門的軟體超越數學家”,成為證明的構建者,他說。“當這種情況發生時,你所思考的證明之死將被避免。我想這是一場慘勝。”
最近,我請一位數學界的朋友邁克爾·哈里斯給我寫一段話,談談“證明之死”是如何成立的。哈里斯回覆說:“碰巧的是,我最近一直在思考這個問題。 我不確定我是否能用少於1000個字來表達清楚,而且任何少於10000個字的內容都只是一連串的謎語。”
他正在組織一場公眾討論會“數學的機械化”,將於10月在紐約市的螺旋中心舉行。公告指出,一些數學家已經提出“對這個行業進行徹底的反思,要求未來的證明以計算機可讀的程式碼編寫。一些數學家甚至預測,人工智慧將取代人類從事數學研究,就像在許多其他活動中一樣。”公告繼續寫道:
一個人對未來證明機械化的可能性的立場取決於一個人對數學本身的看法。數學是一種手段,一個稱職的機器可以像人類一樣好,甚至更好,地實現這個目的嗎?如果是這樣,那麼這個目的是什麼?為什麼機器被認為比人類更可靠?或者,數學反而是一種目的本身,一種為了其內在價值而追求的人類實踐?如果是這樣,那麼這種價值可能是什麼?它能與機器分享嗎?
很棒的問題。我會去那裡,收集“證明之死重灌上陣”的素材。我不得不做出一個讓步。 霍根曲面反駁了我的證明之死論題,但方式與霍夫曼和卡徹的意圖不同。數學可能正在超越我們的認知能力,機械化可能正在逼近,但人類仍在發現和證明新事物的存在。這讓我很高興。
延伸閱讀:
好吧,也許證明並沒有消亡 [後續文章]
身心問題 (免費線上書籍)