如果要您選擇幾個詞語或符號來概括您的遺產,您會選擇什麼?約翰·卡爾·弗里德里希·高斯(Johann Carl Friedrich Gauss,1777–1855)身後留下了無數數學成就可供選擇,但他最希望的是在他的墓碑上蝕刻一個“正十七邊形”。這個高度對稱的17邊形在他認為是對數學最偉大貢獻之一的證明中扮演了重要角色。在年僅18歲時,高斯利用正十七邊形解決了一個困擾數學家超過2000年的經典問題。回顧這段歷史,揭示了古代將形狀概念化為圖畫的方式與現代用方程來管理形狀的觀點之間存在的深刻聯絡。
古希臘幾何學
古希臘人在幾何學方面非常出色,特別強呼叫圓規和直尺進行的作圖。可以將這些作圖視為具有所需幾何特性的圖表,僅用書寫工具和兩種工具建立。給定兩個點,繪圖圓規(不要與導航裝置混淆)允許人們建立一個以任一點為圓心並穿過另一點的圓。直尺可用於在點之間繪製直線。這兩種工具都沒有任何標記,因此人們無法用它們測量距離或角度。
關於支援科學新聞事業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞事業 訂閱。透過購買訂閱,您將有助於確保未來能夠繼續講述關於塑造我們當今世界的發現和思想的具有影響力的故事。
在所有可以用圓規和直尺構造的形狀中,正多邊形具有特殊的地位。
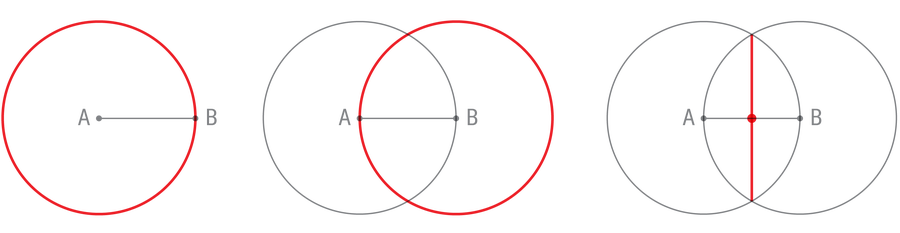
希臘人並非為了讓數學更具挑戰性而強加武斷的規則。用圓規和直尺構造形狀的遊戲起源於公元前三世紀歐幾里得的幾何原本,這是有史以來最重要的教科書之一。與現代數學家一樣,歐幾里得著手從最少的假設中推匯出所有幾何學。歐幾里得不是僅僅斷言形狀或其他幾何物體的存在,而是想用最簡單的成分:直線和圓,明確地構建它們。為了感受這些作圖,請親自嘗試一個:找到下面從A到B線段的中點。目測是不夠的;你的方法必須確定精確的中點。
首先使用圓規畫一個以A為圓心並穿過B的圓。然後重複此步驟,畫一個以B為圓心並穿過A的圓。這些圓將相交於兩點。使用直尺連線這兩點。由於構造中的對稱性,這條垂直線將精確地與原始線段的中點相交。

Amanda Montañez
Amanda Montañez
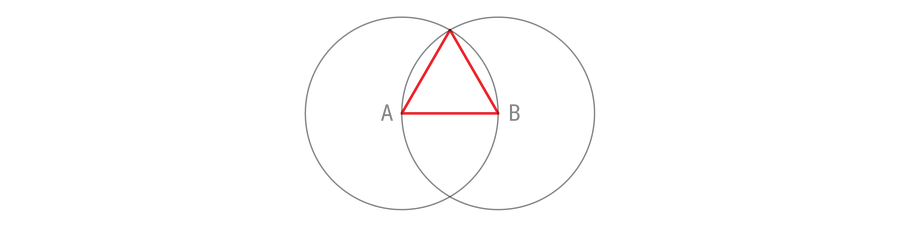
這個練習不僅僅是平分一條線段。它在兩條線之間建立了一個直角,這對於如此受限的工具集來說並非易事。透過連線更多的點,您可以製作一個等邊三角形——一個邊長相等且角相等三角形。
Amanda Montañez
請注意,三角形的每條邊也是其中一個圓的半徑。這些圓的大小相同,因此三角形的所有邊都具有相同的長度。因此,等邊三角形可以用圓規和直尺構造,Q.E.D. 恭喜您堅持完成了歐幾里得《幾何原本》第一卷中的第一個命題。還有13卷要看。
一個障礙
在所有可以用圓規和直尺構造的形狀中,正多邊形具有特殊的地位。多邊形是由直線邊組成的封閉形狀,例如三角形和矩形(與圓形等曲線形狀或字母E等非封閉形狀相對)。正多邊形具有最大的對稱性,因為它們的邊都具有相等的長度,並且它們的角都具有相等的度量(例如正方形和等邊三角形,但與矩形和菱形不同)。用圓規和直尺構造任何舊的不規則三角形都是小菜一碟——只需在頁面上散佈三個點並將它們用線連線起來即可。但是構造我們完美對稱的等邊三角形——一個正多邊形——需要一些優雅的準備工作。
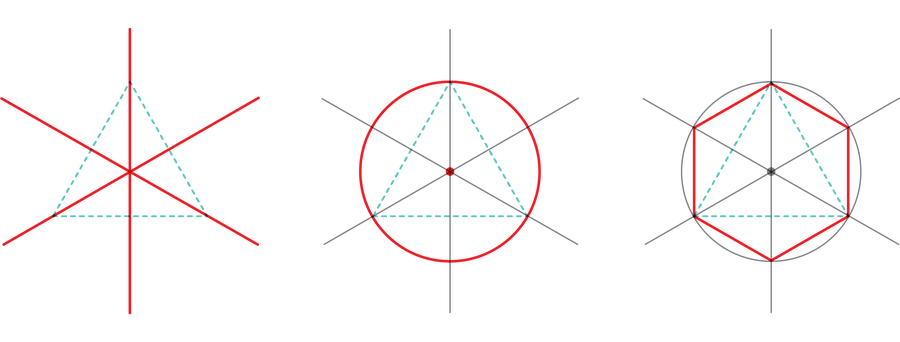
歐幾里得弄清楚瞭如何構造具有三、四或五條邊的正多邊形——分別是等邊三角形、正方形或正五邊形。他從這些核心構造中擠出了一些更多的概括;例如,一旦你在頁面上有一個正多邊形,一個簡單的操作將產生一個新的邊數是原來兩倍的正多邊形。
Amanda Montañez
您可以根據需要多次重複此加倍過程。這意味著三邊形、四邊形和五邊形的正多邊形可以轉換為六邊形、八邊形和十邊形的正多邊形,以及十二邊形、十六邊形和二十邊形的正多邊形,等等。歐幾里得還展示瞭如何“乘”三邊形和五邊形的正多邊形以產生正十五邊形。
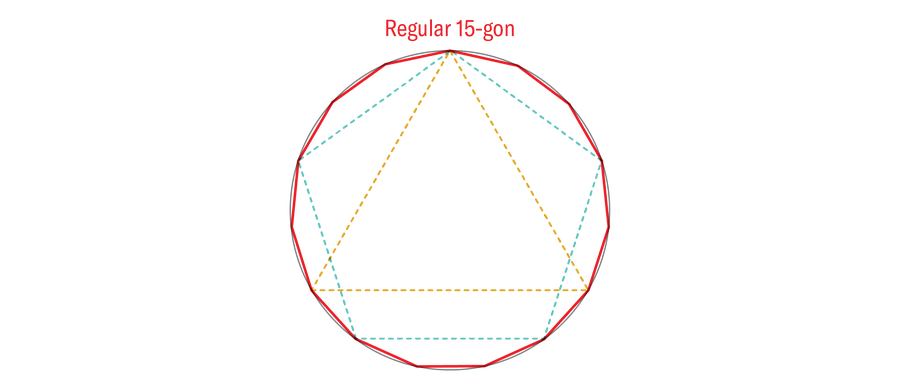
Amanda Montañez
進展到此為止停滯了。不知何故,歐幾里得知道原則上可以構造一個正3072邊形(一個三角形加倍10次),但他不知道如何構造正七邊形(heptagon)或正十一邊形(hendecagon)。需要明確的是,邊數大於二的任何正多邊形都存在,並且可以用更強大的工具構造。歐幾里得遺留的問題是,哪些可以用圓規和直尺單獨構造。這個問題在兩個千年裡一直沒有得到解答,直到一位德國少年拿起鉛筆。
18世紀的數學來救援
到1796年,還沒有新的正多邊形加入到可構造形狀的行列中,但數學家們對圓規和直尺的構造有了更深入的瞭解。高斯知道如何將構造正多邊形的問題簡化為僅建立一個具有非常特定長度的線段。要構造一個17-gon,首先從一個單位圓(半徑等於1)和一個圓上的點A開始,如下面的圖形所示。想象一下,我們可以找到A上方紅色點B,它正好在圓周的1/17處。如果我們能夠從藍色點構造紅色點,我們可以圍繞圓周重複該動作,並用直尺連線這些點:瞧,一個正十七邊形。
但是,給定點A,我們如何繪製點B呢?請注意,如果我們能夠繪製標記為x的紅色線段,那麼我們可以將其連線到紅色點B,我們就成功了。構造正十七邊形的整個問題歸結為建立一個長度精確為x的線段。對於對數學好奇的人來說,x = cosine (2π⁄17)。
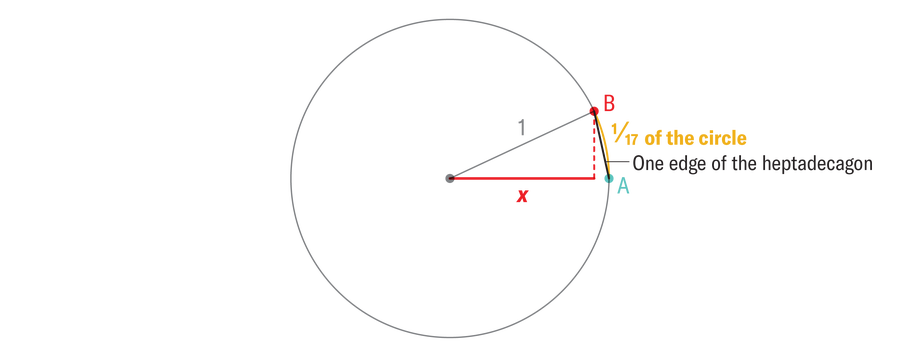
Amanda Montañez
我們可以使用圓規和直尺構造任意長度的線段嗎?到高斯時代,數學家們已經知道這個問題的驚人答案。一個長度可構造的充要條件是它可以表示為對整數進行加法、減法、乘法、除法或平方根運算的結果。因此,一些奇怪的數字,例如99⁄5的平方根,是可構造的(99和5是整數,我們對它們應用除法和平方根),而一些更熟悉的數字,例如pi (π) 和2的立方根,則不可構造,因為永遠無法僅用這五種運算來表示它們。
值得注意的是,古希臘人用來繪製幾何圖形的簡陋工具與現代代數的自然運算完美匹配:加法 (+),減法 (−),乘法 (×),除法 (/) 和開平方根 (√)。原因在於直線和圓的方程僅使用這五種運算,這是歐幾里得在代數前時代無法想象的觀點。
您可能會驚訝地得知,高斯實際上從未繪製過正十七邊形。他不需要這樣做。他透過僅用圓規和直尺允許的五種代數運算來表示特殊長度 x[cosine (2π⁄17)],從而證明了該形狀在原則上是可構造的。即使您不覺得他的方程特別有啟發性,它的複雜性也表明了這位青少年必須為此問題投入了多少工作。

更令人印象深刻的是,高斯完全描述了哪些正多邊形是可構造的,哪些不是(儘管直到1837年,皮埃爾·萬策爾(Pierre Wantzel)才提供了嚴格的證明,表明高斯的描述沒有遺漏任何內容)。因此,高斯不僅描述了所有可構造正多邊形的形式,而且他和萬策爾還證明了長期以來令人困惑的正七邊形(七條邊)和正十一邊形(十一條邊)不可能僅用圓規和直尺構造,正如無數其他形狀一樣,從而證實了歐幾里得的挫敗感。
根據傳記作家G. Waldo Dunnington的說法,高斯對破解這個千年難題感到非常自豪,並告訴一位朋友他希望在他的墓碑上展示一個正十七邊形。遺憾的是,他沒有如願以償,但在高斯的出生地德國不倫瑞克市的一座紀念碑的背面刻著一顆17角星。石匠選擇了一顆星星,因為他認為人們無法區分正十七邊形和圓形。我想知道歐幾里得是否會同意。