通常,數學中有明確的答案——特別是當任務不太複雜時。但是,當涉及到2000年開始流行的睡美人問題時,仍然沒有普遍的共識。哲學和數學領域的專家分為兩個陣營,並不停地引用——通常非常令人信服——各自立場的論據。關於這個謎題已經存在100多篇技術出版物,幾乎每個聽到睡美人思想實驗的人都會形成自己強烈的觀點。
困擾專家們的難題如下:睡美人同意參加一個實驗。週日,她被給予安眠藥併入睡。然後,實驗者之一拋擲一枚硬幣。如果“正面”朝上,科學家們會在週一喚醒睡美人。之後,他們會給她服用另一片安眠藥。如果“反面”朝上,他們會在週一喚醒睡美人,讓她重新入睡,並在週二再次喚醒她。然後他們再給她服用一片安眠藥。在這兩種情況下,他們都會在週三再次喚醒她,實驗結束。
這裡重要的是,由於安眠藥的作用,睡美人不記得她之前是否被喚醒過。因此,當她醒來時,她無法區分是星期一還是星期二。實驗人員也沒有告訴睡美人硬幣投擲的結果或當天是星期幾。
然而,每次她醒來後,他們都會問她一個問題:硬幣正面朝上的機率是多少?
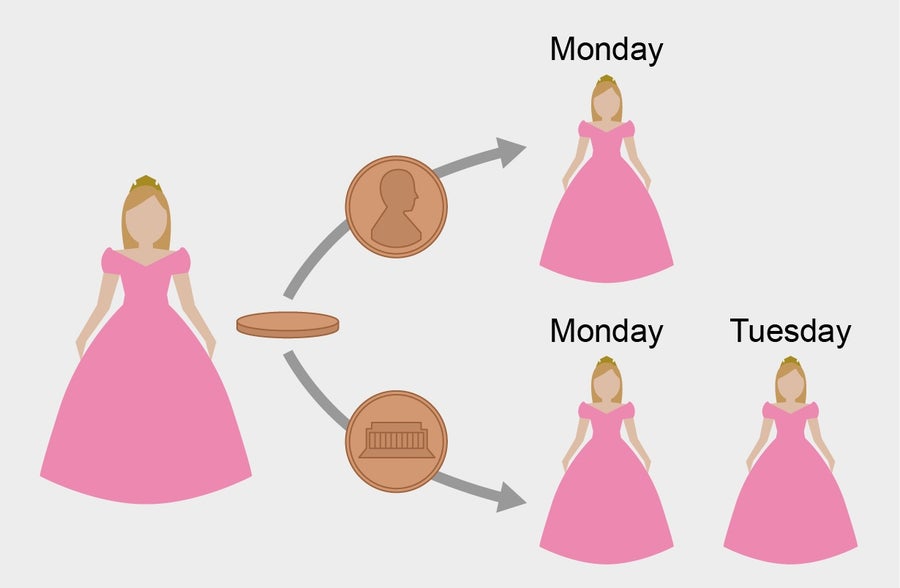
根據硬幣投擲的結果,科學家們會喚醒睡美人一次(正面)或兩次(反面)。 來源:Spektrum der Wissenschaft/馬農·比肖夫,由《大眾科學》設計
把自己放在睡美人的位置:你醒來,你不知道是星期幾,你也不知道你之前是否被喚醒過。你只知道實驗的理論過程。
我的第一直覺是睡美人應該猜½。無論實驗的其餘部分如何,硬幣正面或反面朝上的機率始終為50%。美國哲學家大衛·劉易斯在得知這個問題時也持有相同的觀點。畢竟,甚至可以在送睡美人睡覺之前拋擲硬幣。根據實驗的設計,她沒有任何額外的線索來了解情況,因此邏輯上她應該將機率定為½。
但是,也有令人信服的論據支援機率為⅓。如果你仔細思考睡美人的經歷,那麼可能會發生三種情況
她在星期一醒來,拋擲的是正面。
她在星期一醒來,拋擲的是反面。
她在星期二醒來,拋擲的是反面。
每種事件的機率是多少?你可以從數學上和經驗上對此進行研究。假設你拋擲硬幣100次,得到反面52次,正面48次。換句話說,星期一/正面情景發生48次,而星期一/反面和星期二/反面情景各發生52次。
由於星期二/反面總是緊隨星期一/反面之後,因此所有三個事件的機率都是相等的——因此必須是⅓。當睡美人被喚醒並被要求回答硬幣投擲正面朝上的機率是多少時,根據這種推理,她應該回答⅓。

如果在100次拋擲後,你得到正面48次,反面52次,你可以將這些數字應用於睡美人的星期一和星期二情景。你會發現這三種情況或多或少同樣可能發生。 來源:Spektrum der Wissenschaft/馬農·比肖夫,由《大眾科學》設計
普林斯頓大學的科學哲學家亞當·埃爾加,他在2000年普及了睡美人問題,得出了這個結論。他以數學上合理的方式闡述了他的論點。如果睡美人醒來時被告知今天是星期一(M),那麼星期一/正面(M,H)和星期一/反面(M,Z)的機率無疑是相等的:P(M,H)= P(M,Z)= ½,其中P代表機率。另一方面,如果睡美人醒來並得知拋擲的是反面,那麼那天可能是星期一或星期二(T),這意味著P(M,Z)= P(T,Z)= ½。
根據條件機率的計算,由此得出,在一般情況下(睡美人沒有收到任何額外資訊的情況下),這三個值是相等的:P(M,Z)= P(M,H)= P(T,Z)。由於所有三個機率必須加起來為1,因此每個單獨的值為⅓。換句話說,由於在反面的情況下,睡美人被喚醒的次數是正面的兩倍,因此從埃爾加的觀點來看,她應該回答⅓。
走向極端
既然你已經聽到了兩個主要的論點,你現在會如何回答這個問題?為了更好地理解睡美人問題,思考更極端的思想實驗版本可能會有所幫助。
假設在反面的情況下,睡美人不僅會在第二天額外被喚醒和提問一次,而且會被喚醒一百萬次(大概以更小的時間間隔——因為即使對於童話人物來說,這個時間表也是殘酷的)。如果你喚醒她並問她硬幣正面朝上的機率是多少,那麼答案½在這種情況下似乎不合邏輯。如果硬幣投擲結果為反面,睡美人會被連續提問一百萬次,而在正面的情況下,她只會被提問一次。
但是極端情況也可以加強½陣營的立場。例如,可以使用體育博彩代替拋硬幣,例如退役短跑運動員尤塞恩·博爾特對陣歌手泰勒·斯威夫特的賽跑。在這種情況下,如果博爾特(多項跑步類別的世界紀錄保持者)擊敗這位流行歌星——正如大多數人所預期的那樣——睡美人只會在星期一醒來一次。但是,如果與所有預期相反,斯威夫特證明更快,睡美人必須每天醒來一個月,連續30次。博爾特輸給斯威夫特的機率非常低。但是,如果我們應用與激勵⅓回應相同的邏輯,我們需要同等看待這些情景。睡美人仍然需要在醒來後押注斯威夫特獲勝,因為在這種——誠然不太可能的——情況下,她可能會被喚醒30次。劉易斯認為這個論點是荒謬的。因此,他認為這個思想實驗支援½陣營。
你現在完全困惑了嗎?你不是孤身一人。你的觀點改變了嗎?我的改變了。無論如何,我不再完全信服½陣營。我也能從⅓立場中獲得啟發。
這個謎題有一些有趣的應用。哲學家和數學家可以用它來廣泛地思考決策和機率。例如,這個思想實驗說明了一個人的信念——在這種情況下是睡美人的信念——如何導致不止一個理性的結論。它還強調了實驗可能性的數量(例如拋擲正面與反面)與實驗內部某人的可能經歷之間的差異。
本文最初發表在《光譜》雜誌上,並經許可轉載。
