2018年,據報道,在紐約市,一隻貓從32層公寓的窗戶墜落到堅硬的瀝青路面上——並倖存了下來。在獸醫那裡接受了兩天的治療,獸醫治療了它的肺塌陷和牙齒斷裂後,這隻四條腿的朋友得以重返家園。其他類似的事件很可能促成了貓有九條命的說法。幾十年來,來自廣泛學科的研究人員一直試圖瞭解它們驚人的生存技能。
但讓19世紀末的物理學家感到困惑的,並非動物從令人眩暈的高度墜落。相反,專家們被貓在墜落時繞自身軸旋轉然後腳先著地的照片難住了。當時的影像顯示,一個人抓住貓的腿,使其背部朝向地面。然後將動物放開。起初,貓科動物背部朝下,倒懸在空中。但在接下來的照片中,發生了一些似乎違反物理定律的事情:貓翻身並腳先著地。
當然,人們從日常觀察中知道,這些四足動物可以在空中翻身。但人們一直認為,它們是透過從墜落的表面上蹬踏來獲得這種運動所需的動量。這是因為根據角動量守恆定律,一個沒有旋轉的物體不可能在沒有外部影響的情況下突然旋轉。然而,這正是照片所顯示的。最初,貓筆直下落。然後它設法繞自身軸旋轉。這怎麼可能呢?
支援科學新聞事業
如果您喜歡這篇文章,請考慮訂閱以支援我們屢獲殊榮的新聞事業 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和思想的具有影響力的故事的未來。
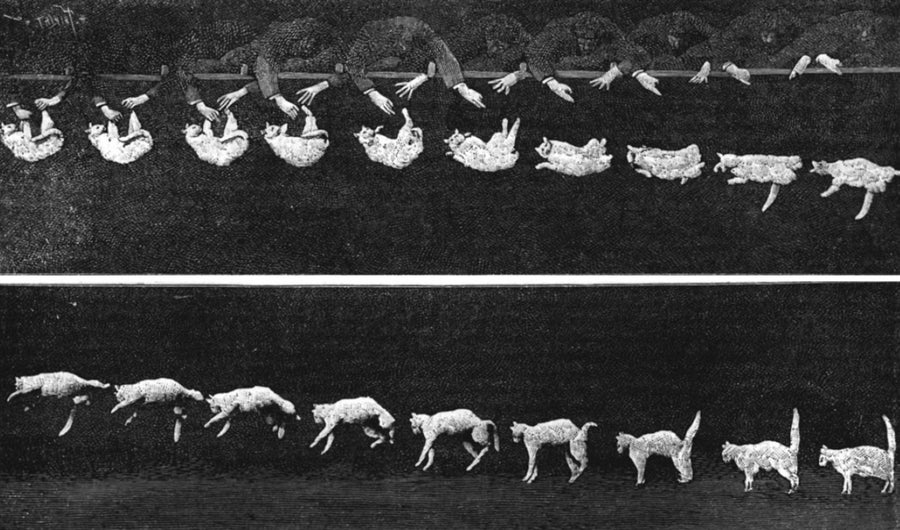
幾十年來,墜落的貓一直困擾著物理學家。這些照片拍攝於 1894 年。圖片來源:The Picture Art Collection/Alamy Stock Photo
這種現象引起了許多科學家的關注,包括以其電磁學研究而聞名的物理學家詹姆斯·克拉克·麥克斯韋。他進行了多次實驗,將貓從不同的高度(包括從敞開的窗戶)掉到床和桌子上。但直到 1969 年,“墜落貓問題”才得到解決。事實證明,人們對貓的身體沒有進行足夠仔細的考慮。它不僅僅是一個神奇地開始旋轉的圓柱形物體。如果您仔細觀察,您會發現貓的上半身和下半身朝相反的方向旋轉。因此,角動量守恆定律得以保留。如果動物像胡椒研磨器一樣朝兩個不同的方向旋轉,則角動量的變化為零。
但是貓是如何設法腳先著地的呢?為了做到這一點,貓科動物利用了經典力學的物理定律:透過將前爪靠近身體,它們減小了慣性矩。就像花樣滑冰運動員一樣,它們的上半身繞自身軸快速旋轉。然後,動物用後腿採用相反的效果。它們伸展腿部,以產生儘可能大的慣性矩。結果,上半身旋轉了很大的角度,而後腿朝相反的方向旋轉的角度較小。動物極其靈活的脊柱使這種運動成為可能。一旦上半身處於正確的位置(即頭部在地面上方垂直對齊),貓就可以伸出前爪,收緊後腿,並朝相反的方向執行類似胡椒研磨器的運動,從而使後爪也在地面上方對齊。透過這種方式,動物總是設法四肢著地——遵循所有物理定律。
貓能從多高的高度墜落並倖存下來?
物理定律表明,墜落高度越高,衝擊力越大。但 1980 年代的一項研究描繪了不同的景象——至少對於貓而言是這樣。兩位紐約市獸醫描述了 1984 年 6 月至 11 月期間共 132 例貓從高層建築的 32 層樓墜落的案例。總體而言,90% 的貓倖存了下來。當獸醫記錄傷情時,他們做出了一個令人驚訝的觀察:雖然損傷的嚴重程度在約七層樓的高度內有所增加,但之後似乎有所下降。換句話說,從 11 樓墜落對貓來說可能比從 6 樓墜落更溫和。
貓科動物似乎再次打破了物理定律。身體墜落的樓層越高,受到地球引力加速的時間就越長。因此,它的速度應該越來越快,直到最終撞擊地面。突然的撞擊將動物從墜落中獲得的動能轉化為其他形式的能量,這可能導致骨折、肺塌陷以及更糟的情況。因此,從高層墜落應該比從低層墜落產生更令人不快的後果。
但是,這種思考貓科動物自由落體的方式忽略了空氣阻力。畢竟,貓不是在真空中墜落到地面,而是在空氣中移動,空氣可以減緩它們的墜落速度。因此,在貓墜落過程中,有兩個相反的力作用在它身上:重力Fg和阻力FR,阻力會減慢它的速度。雖然Fg的形式非常簡單,僅僅是貓的質量m和重力加速度g的乘積,但空氣阻力取決於橫截面積A、阻力系數cW、空氣密度ρ和墜落物體的速度v:FR = ½ x ρ x A x cW x v2。在墜落開始時,貓的速度為零,因此只有重力加速度作用於它,但是隨著v的增加,相反的摩擦力就會顯現出來。因此,要確定動物的具體運動,必須計算總力(Fg – FR)。然後,這決定了作用在一定重量m的貓身上的加速度:m x a = Fg – FR。
墜落貓的速度極限
加速度對應於速度的變化,可以用導數在數學上表示,a = d⁄dt v。因此,如果您想計算貓在某個時刻的速度,您必須求解一個複雜的方程組,該方程組既包含速度本身又包含其導數(加速度):m x d⁄dtv = m x g −½ x ρ x A x cW x v2。對於這種微分方程,通常沒有精確解。在這種情況下,可以計算對應於雙曲正切的速度解。根據貓的橫截面和體重,您最終會得到一條曲線,該曲線在開始時快速增長,然後趨於平緩並收斂到恆定值:動物在墜落開始時速度很快增加,然後空氣阻力最終變得非常強,以至於它不再加速,正如東南路易斯安那大學的物理學家萊特·阿蘭為Wired計算的那樣。
.png?w=900)
貓從更高的高度下降時,速度不一定會更快。圖片來源:Spektrum der Wissenschaft/馬農·比肖夫,Buckyball Design 設計
您還可以非常容易地計算出這個末速度或最大速度限制。因為當摩擦力與重力完全相等時,就會產生末速度,在這種情況下,這兩個力相互抵消,墜落的物體以恆定速度墜向地面。因此,您只需要求解方程 m x g = ½ ρ A cW v2中的v,您就會得到:v = √(2mg⁄ρAc)。
要給出貓的末速度的具體值,只需要插入變數的數值即可。雖然可以估計貓的體重和橫截面積,但阻力系數更難確定。假設一隻貓重 4 公斤(約 8.8 磅),長 50 釐米(約 19 英寸),寬 15 釐米(近 6 英寸)。這些測量值將使動物的橫截面積為A = 0.075 平方米。貓也可能具有圓柱體的阻力系數 (cW = 0.8)。那麼動物的最終速度為:v = 32.68 米/秒,相當於略低於 120 公里/小時(或 74.5 英里/小時)。
為了找出貓在什麼高度達到這個末速度,可以求解微分方程,從而計算出作為墜落高度函式的撞擊時的速度。
.png?w=900)
可以根據貓的墜落高度計算出貓科動物的末速度。圖片來源:Spektrum der Wissenschaft/馬農·比肖夫,Buckyball Design 設計
從圖中可以看出,貓在 100 米的墜落高度時已經達到了 30 米/秒的速度。由於已經觀察到貓從更高的建築物(例如從 32 樓)墜落後倖存下來,因此理論上它們可以在最大可能的 120 公里/小時的末速度下倖存下來。因此,從理論上講,這些動物可以從任何可以想象的高度墜落中倖存下來。
實際效應還是倖存者偏差?
但是,這種末速度計算並不能解釋紐約獸醫的觀察結果:為什麼貓似乎從七樓或更高樓層墜落比從較低樓層墜落更能倖存下來?一種解釋涉及動物的經驗。
當貓從較低的高度墜落時,它會在短時間內處於失重狀態。因此,本能地,它會伸出下面的腿以四肢著地。然而,在高墜落高度下,這種策略沒有用:對齊的腿可能會導致嚴重的傷害,因為動物的重量分佈不當。這種差異可能解釋了為什麼生存率會隨著高度的增加而降低——至少在七層樓以內是這樣。但是,在更高的墜落高度下,摩擦力在墜落過程中變得明顯。這就是為什麼,獸醫推測,貓不再有墜落的感覺。因此,它可以放鬆,並且不會伸展腿。它著陸更柔和,重量分佈更均勻,因此,生存機會更高。
但是,對於這種觀察結果還有一種更簡單的解釋——儘管對於動物愛好者來說,這是一種更令人沮喪的解釋。獸醫的發現可能反映了所謂的倖存者偏差。如果一隻貓從高層墜落並當場死亡,主人可能不會費心去獸醫診所。因此,未報告的死亡人數可能高於醫療專業人員記錄的人數。
本文最初發表於《科學世界》,經許可轉載。
