在高中統計學課上,我的老師提出了一個機率問題,至今仍困擾著我。這是一個謎題,靈感來源於電視遊戲節目《讓我們做個交易》,並以其長期主持人,已故的蒙提·霍爾的名字命名。設定很簡單
您面前有三扇門。

其中一扇門後是一輛新車。另外兩扇門後是山羊。
主持人邀請您選擇一扇門,任意一扇門。

假設您選擇了一號門。

主持人打開了您未選擇的其中一扇門,露出一隻山羊。

然後主持人給您選擇,是否將您的選擇改為二號門。
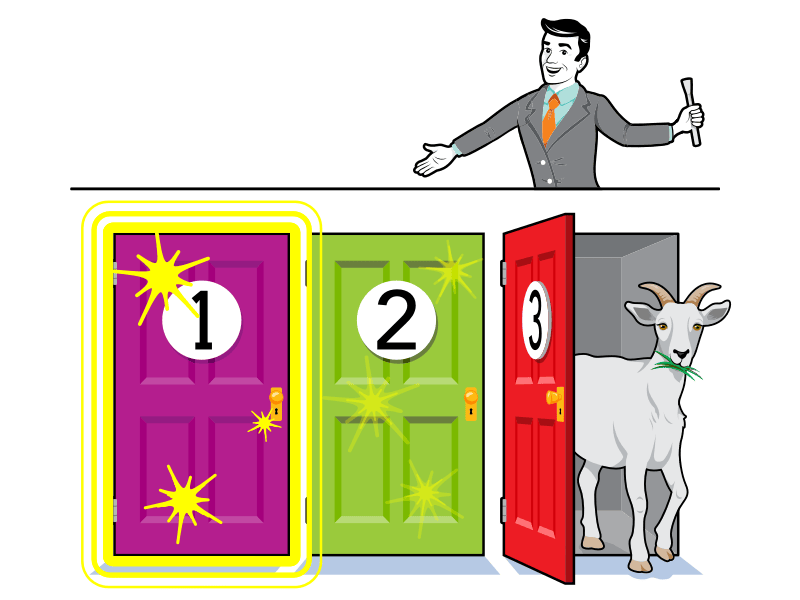
您應該堅持選擇一號門,還是應該換成二號門?
大多數人認為堅持最初的選擇還是換成另一扇未開啟的門都無關緊要,因為機率是五五開——這只不過是擲硬幣而已。但您應該總是換門。如果您換門,您有三分之二的機率獲勝;如果您不換門,則只有三分之一的機率獲勝。換句話說,換門會讓您的獲勝機會翻倍。
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
這個違反直覺的問題,最早在1975年與電視節目聯絡起來描述,在世界各地的入門數學和統計學課程中都有教授。但它在1990年《Parade》雜誌上被廣泛普及。在作家瑪麗蓮·沃斯·薩文特在她的“問瑪麗蓮”專欄中寫到這個謎題後,她收到了約10,000封憤怒的信件,宣稱她給出的答案是錯誤的,其中包括約1,000封由擁有博士學位的人簽署的信件。整個事件非常引人注目,以至於登上了《紐約時報》的頭版。
機率怎麼不是五五開呢?自從那個命運攸關的專欄以來,數學家、心理學家和哲學家一直在試圖理解是什麼讓這個答案如此難以理解。他們發現,一些最常見的認知偏差可能是罪魁禍首,以及對機率如何運作的核心誤解。“幾乎每個人,即使是那些受過良好數學訓練的人,對蒙提霍爾困境也會採取錯誤的直覺方法,”惠特曼學院的比較心理學家沃爾特·赫布蘭森說。“而這表明他們擁有一個功能完全正常的人類大腦。”
在過去的十年裡,我一次又一次地重新審視這個問題,我成了所有這些偏見和推理錯誤的受害者。最終,理解為什麼機率不是五五開需要一個令人費解的視角轉變。
最直接地理解為什麼您應該總是換門的方法之一是畫出所有可能的結果。假設您選擇了一號門。有三種可能的現實:汽車在一號門、二號門或三號門後。
如果汽車在二號門後,蒙提·霍爾將開啟三號門,並讓您選擇換成二號門。換門會得到正確的門。
如果汽車在三號門後,蒙提將開啟二號門,並讓您選擇換成三號門。換門會得到正確的門。
如果汽車確實在一號門後,蒙提將開啟二號門或三號門中的任意一扇,並讓您選擇換成他沒有開啟的那扇門。換門會得到錯誤的門。
簡而言之,如果您最初選擇了正確的門(這種情況發生的機率是1/3),當您被提供機會時,您不應該換門。如果您最初選擇了錯誤的門(這種情況發生的機率是2/3),您應該換門。
這個基本的決策樹證明了兩件事:機率不是五五開,而且如果您總是換門,您會更好。然而,心理學研究表明,人們不僅通常認為選擇是五五開,而且他們還決定堅持最初的門,大約佔85%到90%的時間。更重要的是,社會心理學家、維克森林大學的約翰·彼得羅切利說,即使有越來越多的證據表明他們不應該這樣做,他們通常還是會繼續選擇堅持不動。彼得羅切利讓參與者一遍又一遍地玩蒙提霍爾遊戲,讓他們反覆觀察到獎品更常在“換門”後面——但這些參與者花了多次試驗才學會他們應該換門。
然後他用一系列簡單的拋硬幣進行了測試。想象一下,您反覆拋硬幣,每次都押注結果。您需要多久才能注意到硬幣是有偏差的,正面朝上的機率是2/3而不是1/2?
“大多數人認為他們會在大約40次拋擲後開始意識到這一點。但他們並沒有,”彼得羅切利說。他的研究將這種學習不足歸因於他稱之為“當頭棒喝”思維,或反事實思維。在我們做出決定後,我們經常透過告訴自己“如果我選擇了不同的選擇,我可能會贏”來模擬我們沒有做出的選擇的結果。如果您堅持最初的門並輸了,這種反事實可能並不那麼突出,但當您換門並輸了時,它們會非常突出——可能是因為擁有過又失去比從未擁有過感覺更糟糕。彼得羅切利說,這些與現實競爭的替代方案會模糊您的記憶,“您將看不到正在您面前出現的模式。”
即使當他們瞭解問題的工作原理時,許多人也不相信他們應該換門。那是因為上面的解釋,雖然優雅而準確,但並不令人信服——不僅僅是對像我這樣的統計學學生來說。即使是多產的數學家保羅·埃爾德什也栽了跟頭,據他兒時的朋友和同事數學家安德魯·瓦佐尼說。在1999年《決策科學研究所》出版物《決策專線》的一篇文章中,瓦佐尼描述了埃爾德什第一次被他的朋友提出這個問題時變得慌亂,要求解釋他為什麼要換門,然後在瓦佐尼沒有提供解釋時回應“你怎麼了?”。“我說我很抱歉,但我沒有一個常識性的解釋,”瓦佐尼回憶道。
如果您告訴統計學教授您對蒙提霍爾問題感到困惑,他們通常會提供一個常識性的解釋。想象一下有100扇門而不是三扇。只有一扇門後有一輛汽車,其他99扇門後都是山羊。您選擇一扇門,比如,一號門,然後蒙提沿著隊伍走,一扇接一扇地開啟門。他直接跳過了72號門,讓它保持關閉,然後打開了剩下的門。您是想堅持選擇一號門還是換成72號門?在這裡,如果您換門,您真的應該換門。如果您這樣做,您的獲勝機會是99%。
“人們通常會在那時相信您,”詹姆斯麥迪遜大學的數學家傑森·羅森豪斯說,他寫了一本關於蒙提霍爾問題的書。“但這並沒有完全觸及問題核心的數學問題。”
他是對的:在聽完100扇門的解釋後,我相信正確的選擇是換門——但只是勉強相信。五五開的機率的想法有一種引力,我感覺我無法逃脫。我一直被一個令人困惑的問題困住:為什麼我對三扇門中的第一選擇似乎會“影響”我在換門和堅持之間的第二選擇?我的直覺是,機率應該在兩個選擇之間重置,第二個選擇與第一個選擇無關。
“這種[假設]非常自然,而且似乎非常明顯,但實際上是錯誤的,”羅森豪斯說。那是因為蒙提·霍爾知道汽車在哪扇門後,並且他會相應地選擇他的“戲弄揭示”門。如果他沒有這樣做,而是隨機開啟兩扇未選擇的門中的一扇——讓他真正有機會意外地揭示汽車——那麼您的“堅持還是換門”的選擇確實是五五開。但蒙提的知識和約束改變了一切。要完全理解為什麼這是真的,您需要站在蒙提的角度思考。
去年,當我向我的朋友和她的父親——他教軍事戰略和博弈論——解釋我對這個問題的愛恨交加的關係時,我們決定設定遊戲,以便我們可以親自玩它。我把一顆花生M&M放在三個杯子中的一個下面,並扮演了蒙提·霍爾的角色。在斷斷續續地沮喪了10年後,一切終於豁然開朗。
嘗試站在蒙提的角度思考
讓我們再玩一次。這次,您是主持人。
您知道每扇門後是什麼,但玩家不知道。
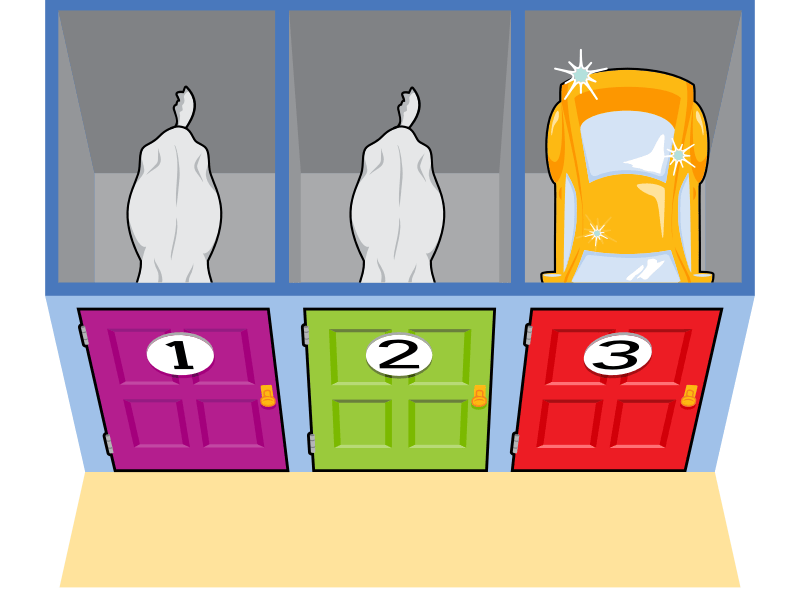
您要求玩家選擇一扇門。
偶爾——平均每三次中一次——玩家會隨機選擇一扇藏有汽車的門作為他們的首選。在這一輪中,那是三號門。
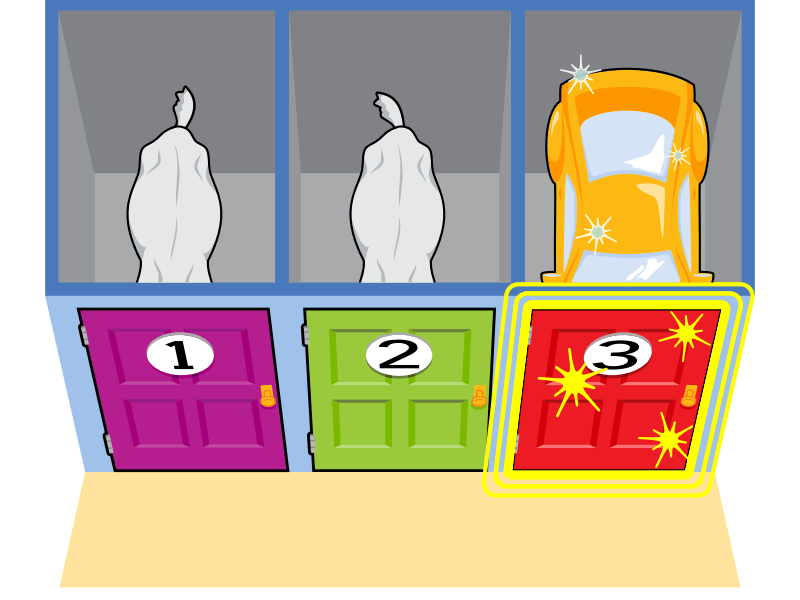
作為主持人,您然後可以開啟另外兩扇門中的任意一扇,因為它們都藏著山羊。(主持人只能選擇揭示山羊。)
您開啟二號門,露出一隻山羊。
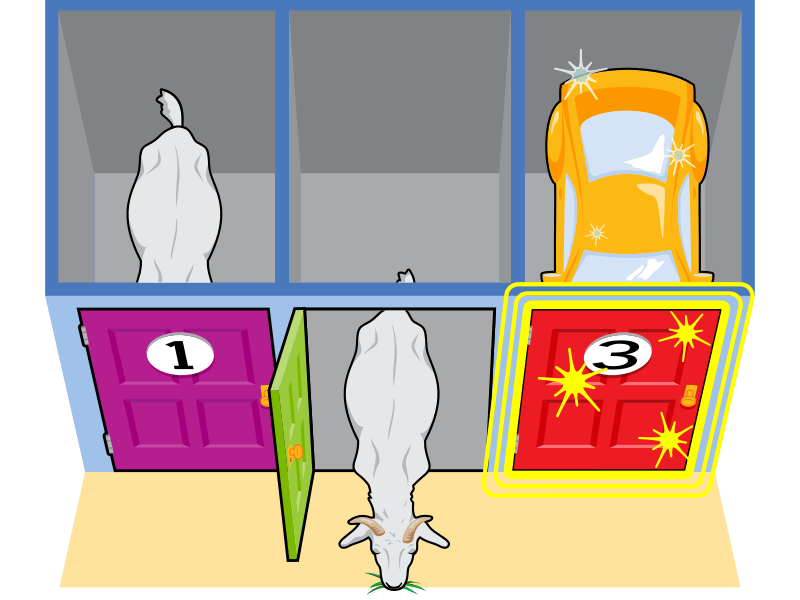
然後您給玩家選擇,是否將他們的選擇改為一號門。

在這種情況下,如果玩家堅持他們最初的選擇,三號門,他們就會獲勝。
但更常見的情況是——每三次中有兩次——玩家會選擇一扇藏著山羊的門作為他們的首選。
讓我們重置遊戲。在這一輪中,玩家首先選擇一號門。

作為主持人,您現在必須開啟另外兩扇門中的一扇。您不能選擇汽車。
因此,作為主持人,您唯一的選擇是三號門。您開啟三號門,露出一隻山羊。
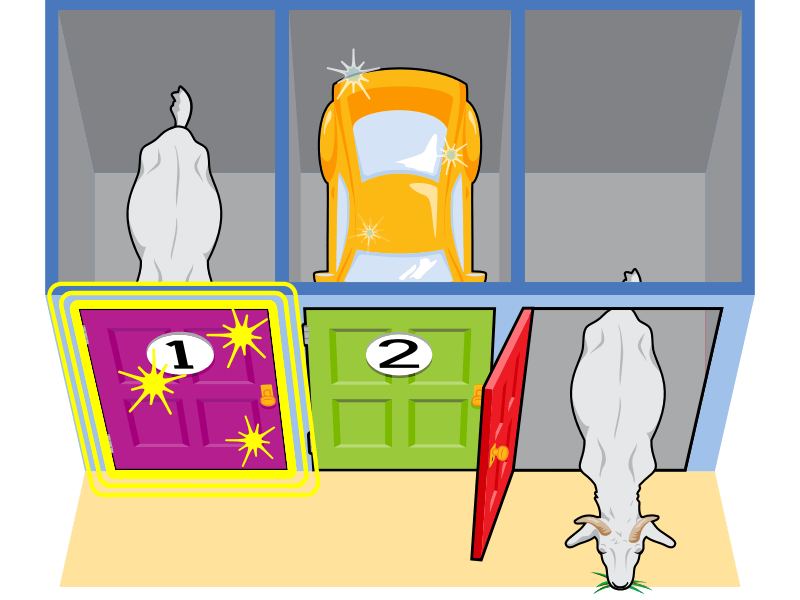
現在您給玩家選擇,是堅持選擇一號門還是換成二號門。
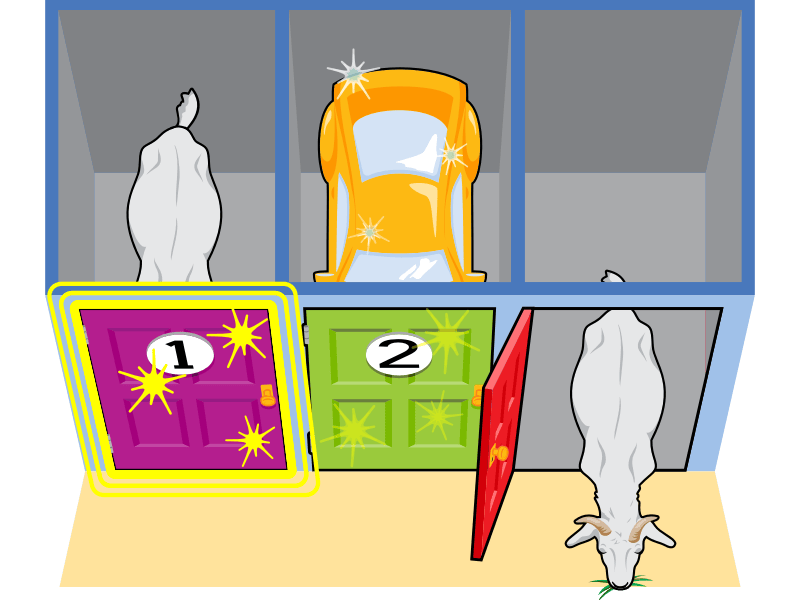
如果他們堅持,他們就會輸。如果他們換門,他們就會贏。
所以,是的,即使在三分之一的情況下,玩家可能會首先選擇汽車,並從不改變主意中獲益……

……但從統計學上講,玩家始終更換他們的門選擇才是最符合他們利益的。
從扮演參賽者轉變為扮演主持人有助於許多人理解為什麼他們應該換門。在2003年的一項研究中,研究人員發現,從蒙提的角度玩遊戲的人比那些作為參賽者玩遊戲的人更傾向於說遊戲節目參與者應該換門。(他們還必須被提示思考如果參與者選擇了三扇門中的每一扇會發生什麼。)彼得羅切利和他的同事在他們自己的研究中也有同樣的經歷。他說,將問題程式設計到他們的研究中,使換門具有如此優勢的原因“非常清楚”。
當您扮演主持人時,您可以看到的是:蒙提·霍爾不是什麼神秘人物,做出一些陰暗的決定來操縱、欺騙或以其他方式欺騙參賽者。事實上,蒙提幾乎沒有做出任何有意義的決定——以至於扮演主持人幾乎很無聊。在三分之二的遊戲中,參賽者第一次選擇了一隻山羊,這意味著主持人在他們開啟哪扇門來戲弄他們時沒有選擇。在三分之一的遊戲中,參賽者第一次選擇了汽車,因此主持人隨機在兩扇山羊門之間選擇進行戲弄揭示。
雖然戲弄揭示對參賽者來說感覺像是新的和重要的資訊,但蒙提看到這只是一種干擾。主持人告訴參賽者一些他們已經知道的事情:“嘿,這兩扇門中的一扇肯定沒有汽車。”作為蒙提,您看到透過開啟一扇山羊門,您不是在給他們資訊——您是在給他們一個機會。
這個機會是以一扇門的價格獲得兩扇門的機率。在這樣的遊戲中,您不能選擇兩扇門。但這實際上是參賽者在決定換門時所做的事情。
像這樣想象一下:您是參賽者,您選擇三號門。然後主持人問您是否想換成一號門和二號門。當然,是的——如果這是一個選項,您當然會選擇兩扇門。然後主持人開啟一號門,露出一隻山羊。您仍然想堅持選擇一號門和二號門,還是換成三號門?您堅持選擇一號門和二號門,因為沒有任何改變。您已經知道您的兩扇門中的一扇包含一隻山羊。那是舊聞了。但您仍然有2/3的機率您的選擇包含獲勝的門。您的兩扇門中的一扇被開啟,而您所有的希望現在都寄託在另一扇門上的事實是完全無關緊要的。
當戲弄揭示門被開啟時,“人們認為一切都改變了,但情況與最初相同,”巴塞羅那大學的心理學家伊麗莎白·圖鮑說。那“是問題中的錯覺”。
“這幾乎就像一個魔術,對吧?”研究邏輯和科學哲學的西方伊利諾伊大學的哲學家克里斯托弗·潘尼斯說。您可能看到面前有兩扇可能的門,但這只是一些巧妙的障眼法。您真正押注的不是一扇門與另一扇門,而是您第一次選擇正確的機率與您沒有選擇正確的機率。您有機會押注您的最初選擇,由於拋棄式的戲弄揭示,兩扇門的機率被摺疊成一扇門。
蒙提霍爾困境在這裡利用了一種叫做等機率偏差的東西:我們假設所有呈現的結果都同樣可能。比利時魯汶大學研究科學方法論和統計學的帕特里克·翁格納解釋說,在一種誇張的形式中,這就像擲骰子,並詢問某人您擲出一點或“非一點”的機率是多少。如果您不瞭解骰子是如何工作的,您可能會錯誤地認為賠率是五五開,因為呈現給您的是兩個選項。但是,一旦您瞭解骰子有六個面,您就會明白這兩個選擇並不等同。
雖然我現在已經獲得了蒙提霍爾頓悟,但以“正確”的方式思考這個問題仍然感覺像是在扭曲我的思維。我仍然固執地回到那個問題:為什麼一旦只剩下兩扇門,機率就不能重置呢?
當我向潘尼斯詢問這個問題時,他的回答揭示了我一生都對機率存在誤解。“想象一下,您[在遊戲進行到一半時]開啟電視,只有兩扇門。您什麼都不知道,您選擇了一扇門,”他說。“那是一個真正的五五開的選擇。您沒有第三個選擇的選項,因為您是在之後才進入這種情況的。”
但與您不同,遊戲節目參賽者如果換門,仍然有2/3的機率做對。那是因為我們一直在談論的機率與門、汽車和山羊無關,而是與觀察者有關。換句話說,機率在觀察者的眼中。
這種更主觀的機率思考方式是所謂貝葉斯推理的核心。托馬斯·貝葉斯牧師是一位生活在18世紀的神學家,他從基於證據的確定程度的角度思考機率。他的定理可以利用事件發生的先驗機率知識,並在新資訊出現時對其進行更新。這種統計方法以個人做出估計為中心——以及這個人對不同結果可能性的瞭解。
今天,貝葉斯定理被用於測試疫苗、繪製宇宙地圖和訓練機器學習演算法。但它不是科學家和數學家處理機率問題的預設方式。這個榮譽歸於一種叫做頻率主義推理的東西,它將機率更像是一種物理屬性,可以透過重複測試或模擬來揭示。這枚硬幣有偏差嗎?頻率主義者多次拋擲它以找出答案。我應該換門還是堅持不動?頻率主義者執行許多計算機模擬,並看到汽車在2/3的時間裡都在“換門”後面。在這裡,這些事件的機率被視為一種物理事物,一種有待發現的客觀真理。
不幸的是,這種方法對揭示蒙提霍爾困境的細微差別幾乎沒有作用。頻率主義者,看著遊戲節目的舞臺,可能會將機率附加到門和汽車上,而不是附加到做出猜測的參與者身上。“我的假設,”瓦佐尼在保羅·霍夫曼的《愛數字的人》中說,“是埃爾德什認為機率是附加在物理事物上的,這就是為什麼他不明白為什麼換門是有道理的。”
當我問1990年《Parade》專欄的作者沃斯·薩文特,她認為蒙提霍爾困境的持久教訓是什麼時,她的回答不涉及統計學中的競爭理論。她說,這個謎題是關於謙遜。“它促進了對人類弱點的一種絕妙展示,”沃斯·薩文特解釋說,“不相信我們可能會犯錯,以及我們堅持早期判斷的頑固,有時甚至是委屈,特別是當我們感覺確定的時候。”