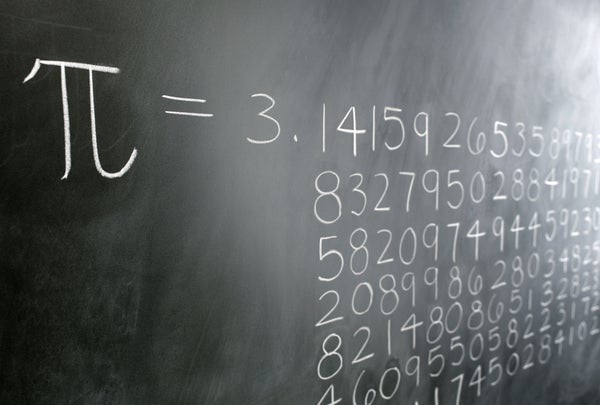簡而言之,pi——寫作希臘字母 p,即 π——是任何圓的周長與直徑之比。無論圓的大小如何,這個比率始終等於 pi。以十進位制形式表示,pi 的值約為 3.14。但 pi 是一個無理數,這意味著它的十進位制形式既不會終止(如 1/4 = 0.25)也不會重複(如 1/6 = 0.166666...)。(精確到小數點後 18 位,pi 是 3.141592653589793238。)因此,為周長與直徑之比使用速記很有用。根據 Petr Beckmann 的《π 的歷史》,希臘字母 π 最初由 William Jones 在 1706 年用於此目的,可能是 periphery(外圍)的縮寫,並在大約 30 年後成為標準的數學符號。
做一個簡單的實驗:用圓規畫一個圓。取一根繩子,將其放在圓上,正好繞一圈。現在拉直繩子;它的長度稱為圓的周長。用尺子測量周長。接下來,測量圓的直徑,即從圓上的任何一點直線穿過圓心到另一側點的長度。(直徑是半徑的兩倍,半徑是從圓上的任何點到圓心的長度。)如果您將圓的周長除以直徑,您將得到大約 3.14——無論您畫的圓有多大!較大的圓將具有較大的周長和較大的半徑,但比率始終相同。如果您可以完美地測量和除法,您將得到 3.141592653589793238...,即 pi。
換句話說,如果您剪下幾段長度等於直徑的繩子,您將需要略多於三段繩子才能覆蓋圓的周長。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
Pi 最常用於某些關於圓的計算中。Pi 不僅關聯周長和直徑。令人驚訝的是,它還透過以下公式將圓的直徑或半徑與圓的面積聯絡起來:面積等於 pi 乘以半徑的平方。此外,pi 經常意外地出現在許多數學情況中。例如,無窮級數的和
1 + 1/4 + 1/9 + 1/16 + 1/25 + ... + 1/n2 + ... 是 π2/6
pi 的重要性至少在 4,000 年前就已被認識到。《π 的歷史》指出,到公元前 2000 年,“巴比倫人和埃及人(至少)已經意識到常數 π 的存在和意義”,認識到每個圓的周長與直徑之比都是相同的。巴比倫人和埃及人都對 pi 的值進行了粗略的數值近似,後來古希臘的數學家,特別是阿基米德,改進了這些近似值。到 20 世紀初,已知大約 500 位 pi 的數字。隨著計算的進步,感謝計算機,我們現在知道超過前六十億位 pi 的數字。