開啟您最喜歡的社交媒體平臺,記下您有多少朋友或關注者。具體來說,記下這個數字的第一位數字。例如,如果您有400個朋友,則首位數字是4,如果您有79個朋友,則是7。假設我們要求很多人這樣做。我們可能會預期各種各樣的回應——普遍的直覺表明,朋友的數量應該在某種程度上是隨機的,因此它們的首位數字也應該是隨機的,1到9均勻分佈。奇怪的是,這不是我們會發現的情況。相反,我們會看到一個明顯的失衡,幾乎一半的朋友數量以1或2開頭,而只有可憐的10%以8或9開頭。請記住,這與擁有更多或更少的朋友無關;1,000個朋友遠遠多於8個。
1和2這種奇怪的過度代表現象不僅限於朋友和關注者,還擴充套件到點贊和轉發,甚至遠遠超出社交媒體,擴充套件到無數個數字世界的角落:國家人口、河流長度、山脈高度、死亡率、股票價格,甚至是典型《大眾科學》雜誌中發現的各種數字集合。不僅較小的首位數字更常見,而且它們還遵循精確且一致的模式。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
如果所有數字都均等地表示,那麼它們中的每一個都將出現九分之一(約11.1%)的時間。然而,在驚人數量的真實世界資料集中,令人震驚的是,30.1%的條目以1開頭,17.6%以2開頭,依此類推。這種現象被稱為本福特定律。即使您更改資料的單位,該定律仍然成立。以英尺或弗隆測量河流,以美元或第納爾測量股票價格——無論您如何測量,這些首位數字的確切比例都保持不變。儘管數學家已經提出了幾個聰明的理由來解釋為什麼這種模式可能會出現,但其純粹的普遍性仍然無法用簡單的解釋來概括。
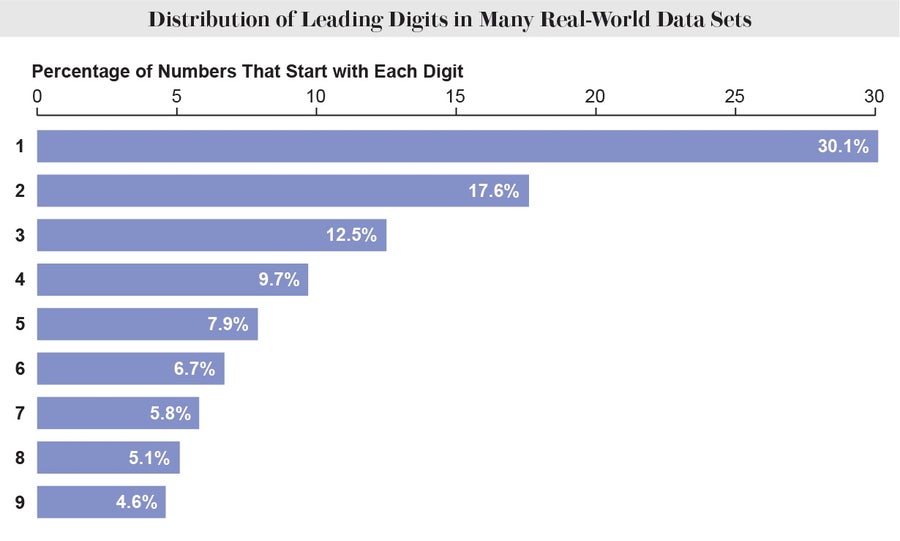
來源:Amanda Montañez;來源:Simon Newcomb在《美國數學雜誌》第4卷第1期,1881年發表的“關於自然數中不同數字使用頻率的註釋” (資料)
碰巧的是,本福特並非第一個發現本福特定律的人。在計算器出現之前,人們將繁瑣的算術外包給稱為對數表的參考書。1881年,天文學家西蒙·紐科姆注意到,對數表的早期頁面(對應於以1開頭的數字)與後面的頁面相比,顯得骯髒和磨損。他推斷,較小的首位數字在自然資料集必然更常見,並且他公佈了正確的百分比。物理學家弗蘭克·本福特在1938年也做出了同樣的觀察並普及了該定律,彙編了超過20,000個數據點來證明其普遍性。
該定律已被用於將人們送入監獄。當檢察官在法庭上辯稱金融顧問韋斯利·羅茲被判犯有欺詐投資者罪時,他的檔案與預期的首位數字分佈不符,因此可能是偽造的。該原則後來幫助計算機科學家詹妮弗·戈爾貝克揭露了Twitter上的一個俄羅斯機器人網路。她觀察到,對於大多數使用者來說,其關注者的關注者數量都符合本福特定律,但虛假賬戶則明顯偏離該模式。本福特定律應用於欺詐檢測的例子比比皆是,從希臘操縱宏觀經濟資料以申請加入歐元區,到I朗2009年總統選舉中的舞弊行為。資訊很明確:有機過程產生的數字傾向於較小的首位數字,而偽造資料的幼稚方法則不然。
為什麼自然界會產生大量的1而缺少9?首先,重要的是要說明許多資料集不符合本福特定律。當以英尺為單位測量時,成年人的身高大多以4、5和6開頭。輪盤賭落在以2開頭的數字上的可能性與落在以1開頭的數字上的可能性相同。該定律更可能適用於跨越多個數量級且從某些型別的隨機過程演變而來的資料集。
指數增長是一個特別直觀的例子。想象一下,一個島嶼最初居住著100只動物,其數量每年翻一番:一年後有200只動物,兩年後有400只。我們已經注意到首位數字的一些奇怪之處。在整個第一年中,島嶼人口的首位數字都是1。在第二年,人口數量在相同的時間長度內跨越了200和300,從而減少了每個首位數字統治的時間。這種情況在第三年繼續,從400到800,此時首位數字的更替速度更快。
原因是,例如,從1,000增長到2,000需要翻一番,而從8,000增長到9,000僅增長12.5%,並且這種趨勢在每個新的數量級都會重置。我們島嶼示例中選擇的引數沒有什麼特別之處。例如,我們可以從43只動物的人口開始,每年增長1.3倍,我們將看到完全相同的首位數字模式。幾乎所有這種型別的指數增長都將趨向於本福特定律。
該定律對測量單位的頑固漠視提供了另一個關於為什麼這種模式在自然界如此常見的暗示。無論我們以米還是英里記錄河流長度,河流長度都遵循本福特定律,而非本福特定律相容的資料(例如成年人的身高)在轉換為米時會徹底改變其首位數字的分佈,因為沒有人是四米高的。值得注意的是,本福特定律是唯一對這種單位變化免疫的首位數字分佈。
我們可以將更改單位視為將資料集中的每個值乘以某個數字。例如,我們將長度集合乘以1,609.34,以將其從英里轉換為米。本福特定律實際上對更一般的變換具有彈性。取符合本福特定律的資料並將每個值乘以不同的數字(而不是固定的數字,例如1,609.34)將不會擾亂首位數字的分佈。這意味著,如果自然現象是由幾個獨立來源的乘積產生的,那麼這些來源中只需要一個符合本福特定律,整體結果就會符合。本福特定律具有蠶食性,就像一堆相乘的數字中的一個零使結果為零一樣。
這些解釋並不能解釋為什麼從《大眾科學》雜誌中挑選出來的各種數字集合會遵守本福特定律。這些數字不會呈指數增長,我們也沒有將它們相乘。數學家特德·希爾發現了許多人認為是首位數字定律的最終證明。他認為,如果您從大量隨機資料集中挑選大量隨機數字,它們將趨向於本福特定律。換句話說,儘管無數資料集顯示本福特模式,但體現它的最可靠方法是從不同的來源提取數字,例如我們在報紙上看到的那些數字。
我已經花了很多時間思考本福特定律,它仍然讓我驚訝於它出現的頻率如此之高。關注您在日常生活中遇到的數字,您可能會開始發現它的例子。
