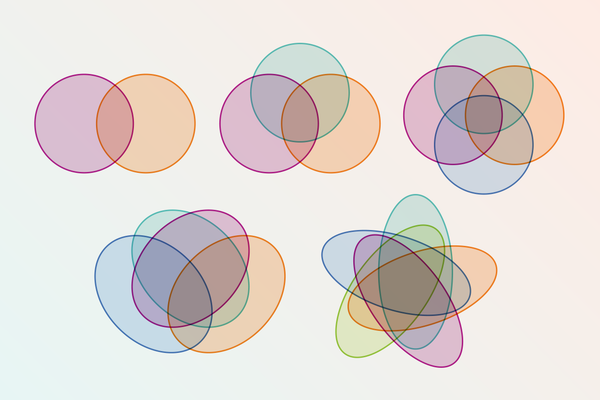在《數學宇宙》一書中,數學家威廉·鄧納姆這樣評價約翰·維恩以其名字命名的遺產——維恩圖:“在漫長的數學史上,沒有人因為更少的東西而更出名。” 雖然維恩圖可能沒有解決任何長期存在的未解難題,但這些相互交錯的圓環當然值得更多讚譽。它們對群體關係的簡潔表示解釋了它們在教室、資訊圖表和網際網路迷因中持久的吸引力。
維恩圖不僅僅是視覺輔助工具,它們還可以幫助我們解決日常邏輯問題,並引發令人驚訝的幾何問題。您見過用四個重疊圓圈組成的合適的維恩圖嗎?沒有,因為這是不可能的。維恩本人發現了這一點,並提出了一個巧妙的解決方案,但這僅僅引發了更深層次的幾何難題,數學家們至今仍在研究。
維恩在1880年首次展示了他的圖表,作為一種視覺化邏輯學當代進展的方法。然後,它們在密切相關的數學分支——集合論中找到了應用,集合論專注於物件的集合。維恩圖通常由重疊的圓圈組成,每個圓圈代表一組元素(例如,可愛的東西或百老匯演出)。兩個圓圈之間的重疊區域包含屬於兩個集合的元素(例如,“貓”)。就像使用統計學中的散點圖或幾何學中繪製形狀一樣,看到問題通常可以澄清問題。
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
想象一下,您正在計劃一個晚宴,並在朋友們善變的偏好中周旋。如果威爾瑪參加,那麼弗雷德也會參加。如果巴尼參加,那麼其他人也會參加。如果威爾瑪來,巴尼就不會來,但如果她不來,他就會來。如果弗雷德和巴尼都參加,那麼威爾瑪也會參加。您應該期望誰會來?當我們只給出文字時,這個難題很難解決。維恩圖提供了一種系統的方法來視覺化和解決它。每個陳述都排除了某些可能的結果,我們透過對維恩圖的相應區域進行陰影處理來表示這些結果。
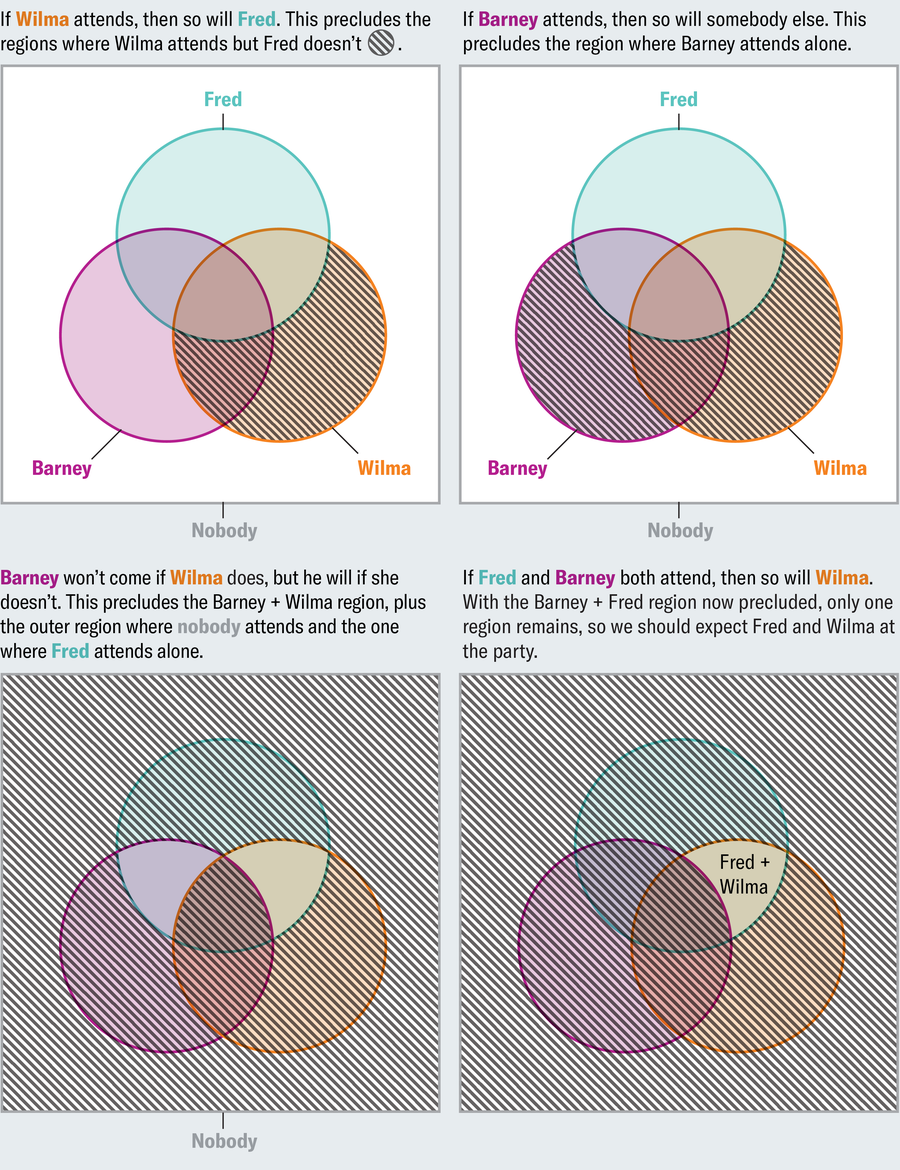
阿曼達·蒙塔涅斯
您遇到的大多數維恩圖都描繪了兩個或三個重疊的圓圈,但是如果您有四個或更多集合要考慮怎麼辦?
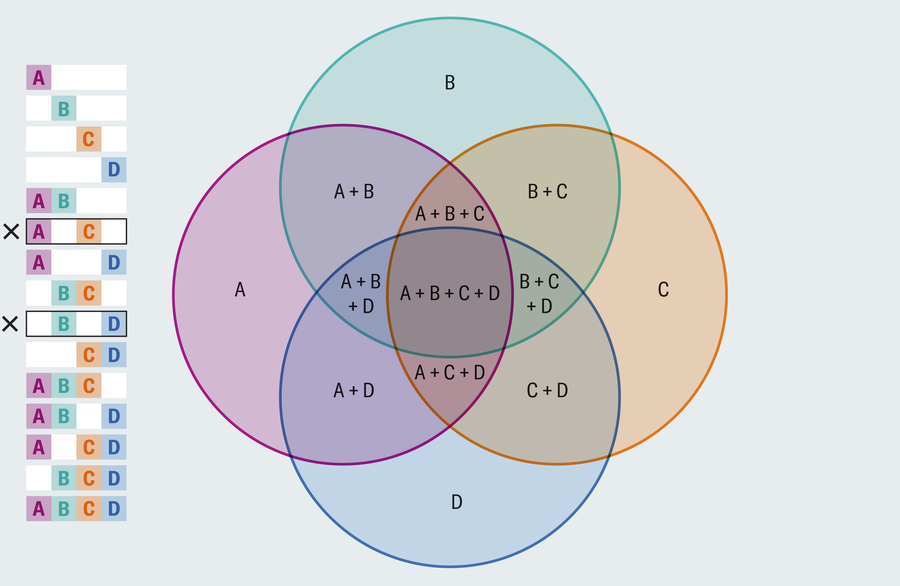
阿曼達·蒙塔涅斯
您發現問題了嗎?沒有一個區域僅包含A和C的重疊,而不包含另一個區域,B和D也是如此。一個合適的維恩圖描繪了所有交叉點的組合。重新調整佈局無濟於事。每個四圓圖都存在同樣的缺陷。
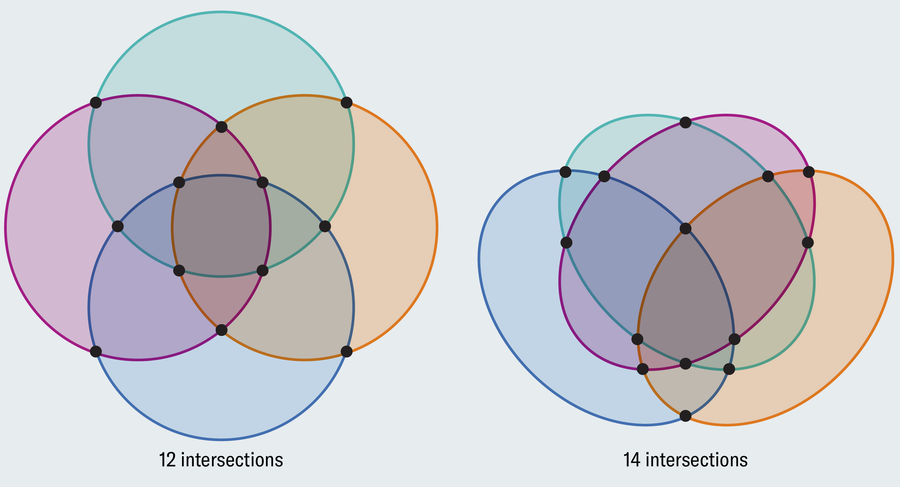
要了解原因,請從一個圓圈開始,並注意它建立了兩個區域——內部和外部。當我們新增第二個元素集合(一個新的圓圈)時,我們將可能性增加了一倍,因此我們需要將區域數量增加一倍(第一個集合、第二個集合、兩個集合和兩個都不是集合)。唯一的方法是讓第二個圓圈在兩點與第一個圓圈相交(僅在一個點接觸將導致只有三個區域:第一個集合、第二個集合或兩者都不是)。這種趨勢持續下去,如果我們想表示所有邏輯可能性,則每個新圓圈都必須使區域數量翻倍。但是新區域的數量不能超過新的交點的數量,並且一個新圓圈只能在兩個點與現有圓圈相交。當新增第三個圓圈時,這很好,因為我們需要新增四個區域,並且新圓圈可以在兩個點與兩個現有圓圈相交,總共四個新的交點。但是,當使用第四個圓圈時,它會崩潰,我們需要八個新區域,但只能聚集六個新的交點。
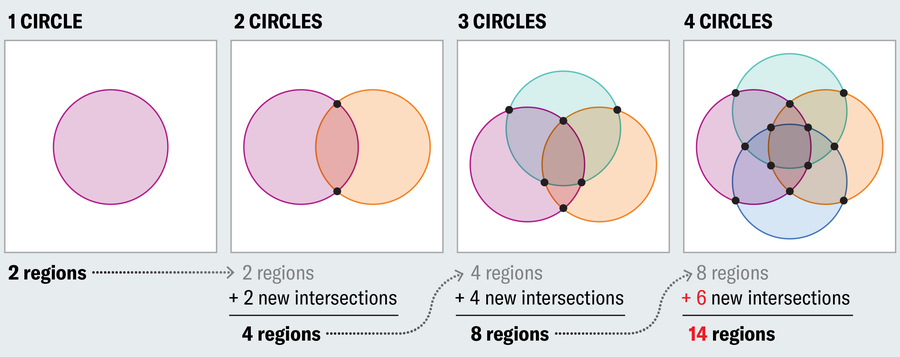
阿曼達·蒙塔涅斯
當然,我們不需要將自己限制在圓圈上。我們可以輕鬆地透過三圓圖追蹤一個彎曲的環,以便它劃分出必要數量的區域,但我們會失去圖表的優雅性。四個相交的球體也可以表示正確數量的區域,但是三維視覺效果很難解析。約翰·維恩知道圓圈的缺點,因此他提出了用橢圓來表示四個集合。
阿曼達·蒙塔涅斯;資料來源:“維恩圖和集合的獨立族”,布蘭科·格林鮑姆著,載於《數學雜誌》,第48卷,第1期;1975年1月 (參考文獻)
與圓圈不同,兩個橢圓可以在四個點相交。這克服了圓圈的侷限性,但這只是暫時的。橢圓適用於四個和五個集合,然後以與圓圈相同的方式失效。隨著集合數量的增長,我們需要越來越奇特的形狀來描繪它們。
有人可能會合理地爭辯說,超過四個元素集合,維恩圖就失去了它們的效用。四橢圓影像已經非常混亂。也許對於五個或更多集合,我們應該放棄視覺表示。但是,效用並沒有像美和好奇心那樣激發數學家的興趣。儘管維恩圖最初應用於邏輯和集合論,但四圓難題提出了一個有趣的幾何學問題。這個種子已經發展成為對維恩圖幾何學的迷人研究,並且一直延續至今。
維恩和他的繼任者認為,橢圓無法描繪五個集合圖所需的所有32個區域。直到1975年,數學家布蘭科·格林鮑姆才透過例項證明他們錯了

阿曼達·蒙塔涅斯;資料來源:“維恩圖和集合的獨立族”,布蘭科·格林鮑姆著,載於《數學雜誌》,第48卷,第1期;1975年1月 (參考文獻)
另請注意,格林鮑姆的圖表顯示出令人愉悅的旋轉對稱性。將其旋轉整整五分之一圈,它又會回到自身,使原始形狀保持不變。典型的兩圓和三圓維恩圖也具有此屬性。將兩圓維恩圖旋轉180度(或將三圓維恩圖旋轉120度),它看起來還是一樣。但是四橢圓圖沒有旋轉對稱性。這可以修復嗎?二、三和五有什麼共同之處,而四沒有?
1960年,當時斯沃斯莫爾學院的本科生大衛·W·亨德森,透過一項驚人的發現回答了這個問題(斯坦·瓦根和彼得·韋伯後來填補了一些空白):只有當集合的數量是素數時,才有可能實現旋轉對稱的維恩圖——素數是隻能被1和自身整除的數字,例如2、3和5,但不是4。亨德森只表明素數個集合是必要的,而不是說您總是可以為每個素數設計對稱的維恩圖。因此,尋找越來越大的示例的競賽開始了。這是一個看起來很狂野的來自彼得·漢堡的11個集合的維恩圖。
南卡羅來納大學的數學家在2004年解決了這個問題,他們證明了對於每個素數個集合都存在旋轉對稱的維恩圖。如果您認為這導致數學家收拾鉛筆,停止對維恩圖的研究,那麼您就沒有繼續關注。相反,社群提高了他們的審美標準,尋求具有更精緻屬性的圖形。
我們開篇引用的內容認為維恩圖被高估了。即使是那些同意這種觀點的人也必須承認它們具有一種奇特的魅力。以邏輯學、幾何學和視覺化中感興趣的主題集合為例,您會在交集處找到維恩圖。