全球數字安全專家都密切關注著 Y2Q——“量子時代還有幾年”——時鐘。它倒計時著預計的日期,屆時量子計算機將能夠破解現代密碼學的一種重要形式。它被稱為公鑰密碼學,因為它具有在公共場合共享金鑰的巧妙方法,當您在網上購物時,它可以保護您的信用卡號安全,並確保您手機的軟體更新來自電話公司而不是駭客。舉報人使用它來聯絡記者,企業使用它來發送機密檔案。
但是量子計算機將使標準的公鑰密碼學型別變得無用。“這真的非常嚴重,”雲安全聯盟量子安全安全工作組聯合主席布魯諾·胡特納說。“如果明天出現量子計算機,我們將無法在任何安全保障的情況下進行對話。”
胡特納是 Y2Q 時鐘的建立者之一,其命名類比於 20 世紀 90 年代末的 Y2K 危機。20 世紀的軟體程式用兩位數字表示年份,這意味著對於計算機來說,2000 年是“00”——與 1900 年相同。涉及此類日期的程式預計在新千年到來時會發生故障,從而可能造成大規模中斷。但最終,當年份改變時,沒有銀行倒閉,沒有電閘道器閉,也沒有飛機從天空墜落。過渡是無縫的——主要是因為企業和政府競相修復了 Y2K 漏洞。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您將幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
沒有人確切知道何時會開發出足夠大的量子計算機來破解密碼學標準。Y2Q 時鐘當前的截止日期 2030 年 4 月 14 日只是一個猜測。但大多數研究人員認為,這種轉變將在未來幾十年內發生。“威脅即將來臨,”胡特納說,Y2Q 時鐘就是一個提醒。“確定一個日期有助於人們集中注意力。”
對於需要長期保密的政府和其他機構來說,真正的截止日期要早得多。如果今天傳送的加密資料被儲存起來,那麼未來的量子計算機可能會追溯解密這些訊息。“如果您需要保守秘密 20 年,並且您認為在 20 年內可能會出現破解您的密碼學的量子計算機,那麼您今天就遇到了問題,”密歇根大學的計算機科學家克里斯·佩克特說。
為了應對這一威脅,美國國家標準與技術研究院 (NIST) 於 2016 年發起了一項公開競賽。它徵集了“後量子”或“抗量子”密碼學的想法——可以在今天的計算機上執行,但非常強大,即使是量子計算機也無法破解的程式碼。為了強調緊迫性,美國國會在 2022 年 12 月通過了《量子計算機網路安全準備法案》,該法案要求政府機構制定過渡到此類演算法的計劃。
經過四輪提交和評估後,NIST 在公鑰加密類別中選出了一個獲勝者,名為 CRYSTALS-Kyber,在用於安全識別訊息傳送者的數字簽名類別中選出了三個獲勝者。NIST 現在正在與研究人員合作,將獲勝的演算法標準化,以便程式設計師可以開始奠定防量子保密的基礎。
然而,令人有些擔憂的是,四個選定的演算法中有三個,包括 CRYSTALS-Kyber,都是基於格數學。專家們相信這些問題非常難以解決——但沒有人能保證未來的突破不會破解它們。
最早已知的密碼學形式之一是用於替換書寫字母的密碼。在凱撒大帝的訊息中,他將每個字母替換為羅馬字母表中三個位置之後的字母。在英語中,這意味著“a”變成“d”,“b”變成“e”,依此類推。要解密來自凱撒的訊息,您只需反轉該過程,將字母移動三個字母位置即可。
凱撒替換方案有無數種變體——在課堂上傳紙條的孩子可以建立自己的方案,用心形替換“a”,用星形替換“b”,依此類推——但它們很容易破解。沒收孩子紙條的老師可能會注意到它包含許多孤立的三角形,代表一個字母的單詞,並推斷出三角形代表“I”或“a”。密碼破譯者通常可以透過比較不同符號的頻率與普通英語文字中字母的頻率來解決更復雜的替換方案。
現代密碼學的黃金標準,稱為高階加密標準或 AES,極大地擴充套件了凱撒的方法。它透過重複替換條目並像洗撲克牌一樣洗牌來打亂訊息。經過足夠的洗牌和替換後,很難重建原始版本。
要解密訊息,您必須透過撤消每次洗牌和替換來解擾訊息。對於一副實體撲克牌來說,這幾乎是不可能的——洗牌順序由細微的動作決定。但是計算機根據一組精確的指令(例如,“將第二個條目移動到第五個位置”)對訊息進行洗牌,這些指令很容易撤消。計算機只需反向執行指令即可:“將第五個條目移動到第二個位置。”
與凱撒密碼一樣,AES 具有對稱的加密和解密程式。它向前和向後應用相同的過程,就像在相反方向轉動鑰匙來鎖定和解鎖門一樣。在 20 世紀 70 年代之前,所謂的對稱密碼學(也稱為對稱金鑰密碼學)是唯一的密碼學型別。但它有一個主要限制:傳送者和接收者需要在交換任何訊息之前,親自或透過可信賴的單獨通訊模式,就加密和解密程式達成一致。
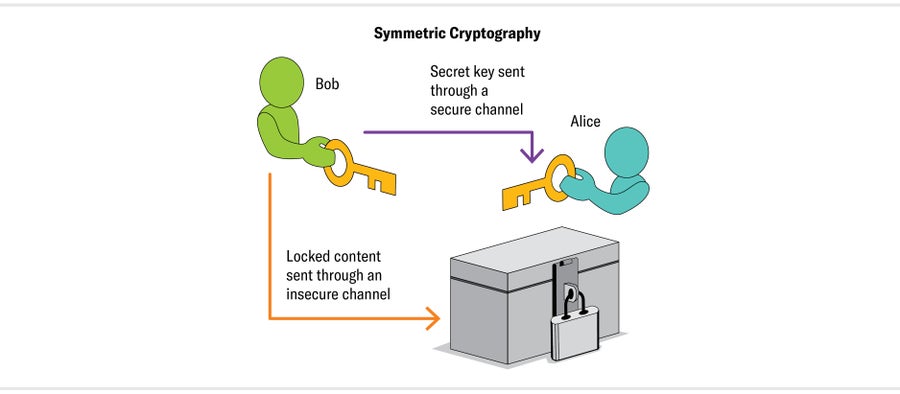
圖片來源:Jen Christiansen
很難想象在沒有這種約束的情況下,對稱密碼學的替代方案。1974 年,加州大學伯克利分校的本科生拉爾夫·默克爾提出了一個課程專案,研究“兩個人如何在沒有任何事先安排的情況下安全通訊”的方法,他預料到這個想法可能顯得多麼離譜,並補充說,“不,我不是在開玩笑。”默克爾設想了一個系統,兩個人完全公開地交換訊息,始終假設有人在監聽。透過這種公開通訊,他們設法建立了一個編碼和解碼方案,並用它來發送秘密訊息。如果其他人正在閱讀這些訊息,他們將無法弄清楚該方案。默克爾的提案因其“不切實際的工作假設”而被一位專家拒絕。
然而,值得注意的是,幾篇數學論文在幾年後就實現了默克爾的願景。提出的兩種演算法,稱為 Diffie-Hellman 和 RSA(Rivest-Shamir-Adleman 的縮寫,其建立者的姓氏),在現代通訊中無處不在。事實證明,甚至在默克爾的課程專案之前,英國情報組織的研究人員就已經發現了這種編碼——公鑰密碼學——並將其保密。
當您線上檢視您的銀行賬戶時,您的計算機和銀行的伺服器正在交換訊息:您傳送您的密碼,銀行傳送您的餘額。當這些資訊在網際網路上傳輸時,其他人可能會讀取它。訊息需要加密。
大多數訊息都使用對稱密碼學(例如 AES)進行加密,這種密碼學可以快速有效地打亂訊息。但首先,您的計算機和通訊伺服器需要就特定的打亂程式達成一致。他們不能簡單地寫下來,因為他們的所有通訊都可能被竊聽者捕獲。他們需要使用公鑰密碼學。
為了理解這個過程是如何工作的,讓我們想象一下,兩個朋友,愛麗絲和鮑勃,擁有一家麵包店,裡面有一個絕密的布朗尼食譜。這個食譜非常秘密,甚至愛麗絲和鮑勃也不知道完整的食譜。他們每個人都新增一種只有新增者才知道的特殊成分。為了製作布朗尼,愛麗絲和鮑勃輪流開始食譜。有時,愛麗絲將基本成分與她的秘密成分混合在一起,然後將麵糊傳送給鮑勃,鮑勃新增他的秘密成分並烘烤。有時,鮑勃先將基本成分與他的秘密成分混合在一起,然後再運送給愛麗絲,愛麗絲混合她的秘密成分並烘烤布朗尼。
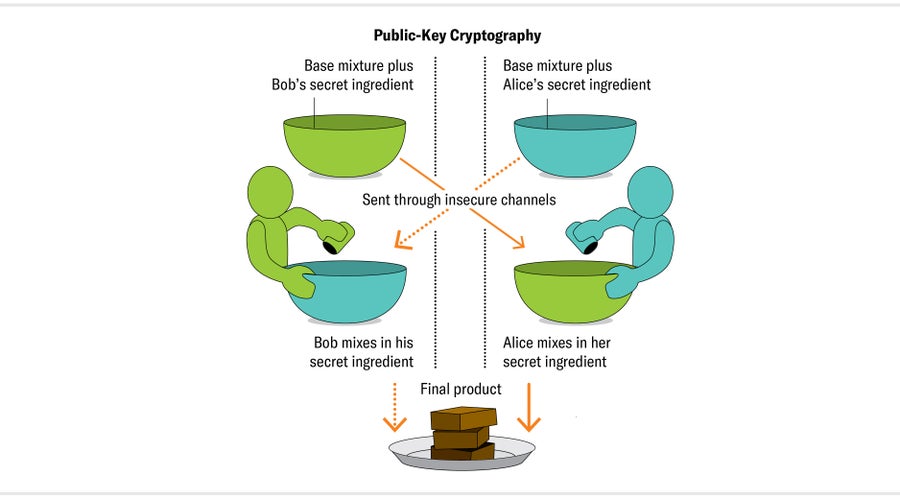
圖片來源:Jen Christiansen
愛麗絲和鮑勃總是得到相同的布朗尼——但他們從不與任何人(包括彼此)分享完整、確切的成分。即使是他們狡猾的送貨司機伊芙也無法弄清楚食譜。(在密碼學中,交換秘密的兩個人傳統上被命名為愛麗絲和鮑勃,而潛在的間諜通常被命名為伊芙。)伊芙無法推斷出秘密成分,因為無論何時她運輸它們,它們都與所有基本成分混合在一起——不可能將它們分開。
當然,計算機不烤布朗尼。它們處理數字和數學。在真正的公鑰密碼學中,目標是最終得到一個共享的秘密數字——類似於授予訪問私人對話許可權的臨時密碼。然後,兩臺計算機可以繼續使用對稱密碼學(例如 AES)進行加密對話。
不同型別的公鑰密碼學以不同的方式建立和共享臨時密碼。愛麗絲和鮑勃透過在運輸前混合成分來向伊芙隱藏他們的布朗尼食譜。實施公鑰密碼學的人將改為使用數學函式來混合秘密數字。
函式就像機器,可以接收數字,攪動它們並吐出一個新數字。公鑰密碼學中使用的函式非常特殊。它們需要在輕鬆混合數字的同時,使其非常難以解混合。即使伊芙看到了函式的輸出,她也不應該能夠猜出哪些秘密數字作為輸入。
例如,RSA 密碼學基於乘法函式及其相反的運算,即因式分解。即使數字非常大,計算機也很容易透過將數字相乘來混合數字。但是,如果數字很大,則撤消乘法運算或因式分解非常困難。(因式分解意味著回答問題:我必須將哪些數字相乘才能得到這個數字?例如,因式分解 21 會得到 3 和 7。)解密使用 RSA 建立的密碼需要因式分解一個大數字。最好的方法是過濾許多數字以找到它們的特定組合——這需要計算機很長時間。
哈佛大學的計算機科學家博阿茲·巴拉克說:“我們實際上已經轉向基於非常非常簡單的東西(如整數因式分解)的密碼學,而不是試圖使密碼學方案越來越複雜,而整數因式分解已經被研究了數千年。”
1994 年,應用數學家彼得·肖爾,時任貝爾實驗室的研究科學家,發現了一種方法,量子計算機可以透過這種方法破解使用 RSA 或 Diffie-Hellman 加密的任何程式碼。正如肖爾告訴我的那樣,他參加了一個關於使用量子計算機解決具有周期性或重複結構的數學問題的講座。這讓他想起了“離散對數”問題。對數函式是指數函式的逆函式——例如,在方程 2x = 16 中找到 x。
通常很容易找到對數,但離散對數問題是關於使用替代算術形式計算對數,在這種形式中,人們像在時鐘上一樣在一個圓圈中計數。正如 RSA 基於因式分解一樣,Diffie-Hellman 基於離散對數問題。計算機科學家普遍認為,使用經典計算機沒有快速找到離散對數的方法。但是肖爾找到了一種在量子計算機上做到這一點的方法。然後,他應用類似的邏輯來展示如何使用量子計算機快速分解大數字。這些解決方案合起來被稱為肖爾演算法。
肖爾並沒有想象要程式設計一臺真正的量子計算機——他只是在黑板和紙上做數學。“當時,量子計算機似乎還遙遙無期,”肖爾說。“所以我主要認為這是一個非常好的數學定理。”但他的演算法對公鑰密碼學具有重大意義。量子計算機可以使用它來破解目前使用的大多數密碼系統。
經典計算機執行在稱為位元的長字串 0 和 1 上,但量子計算機使用量子位元,它是“量子”和“位元”的混合詞。量子位元可以處於疊加態——0 和 1 的奇異組合。透過在兩種狀態之間徘徊,量子位元使量子計算機能夠比經典計算機更快地執行某些任務。但量子計算機很挑剔。量子位元需要在演算法執行時保持疊加態,但它們傾向於“坍縮”成 0 和 1 的字串。
量子計算機看起來令人印象深刻——它們像巨大的金色枝形吊燈一樣從天花板上垂下來——但它們仍然不是很強大。科學家們已經能夠使用少量的量子位元執行計算,並且他們使用肖爾演算法在量子計算機上分解的最大數字是 21。2012 年,英國布里斯托爾大學的研究人員使用量子計算機推斷出 21 是 3 乘以 7。
許多專家認為,足夠大的量子計算機來破解 RSA 和 Diffie-Hellman 將在未來幾十年內建成,但他們很快承認時間表是不確定的。對於需要搶在量子計算機之前的密碼學家來說,這種不確定性令人擔憂。“每個行業都有其工作的某些方面,這對他們來說非常重要,”IBM 的雷·哈里香卡爾說。醫療保健公司需要保護他們在醫學研究中使用的資料,電力公司必須保護電網免受駭客攻擊。“最壞的情況:如果發生不好的事情,他們將完全暴露,”哈里香卡爾說。
每種型別的公鑰密碼學都基於一個難解的數學問題。為了保護秘密免受量子未來的影響,研究人員需要使用非常難解的問題,即使是量子計算機也無法在合理的時間內解決這些問題。NIST 挑戰賽徵集了公鑰密碼演算法的提名,這些演算法可以廣泛地在標準計算機上實施,作為 RSA 和 Diffie-Hellman 的替代方案。人們使用的許多不同的連線系統和裝置都必須“相互交流這種新型密碼學”,NIST 的數學家莉莉·陳說。
在 2017 年的截止日期之前,研究人員提交了 82 種不同的後量子密碼學提案。(令人困惑的是,“量子密碼學”指的是其他東西——使用量子現象作為安全方案的一部分。)在接下來的一年裡,研究人員測試了這些演算法,然後 NIST 專家選擇了 26 種演算法進入下一輪。
公眾意見是 NIST 競賽的重要組成部分。密碼系統不能保證安全,因此研究人員試圖找出其中的漏洞。候選演算法之一使用了“基於同源”的密碼學,這種密碼學已經研究了十年,看起來很有希望。但兩位研究人員注意到,一個 25 年前的數學定理可以用來破解該演算法。他們僅用一臺標準筆記型電腦就花費了一個小時。
NIST 專家最終確定了幾種最終候選演算法,其中大多數基於格數學。“格是一種自然的選擇,”IBM 的瓦迪姆·柳巴舍夫斯基說,他是 CRYSTALS-Kyber 的作者之一。“人們已經在各種偽裝下研究這個問題超過二十年了。”
格是點的重複陣列。最簡單的一種看起來像釘板——點排列成正方形網格。數學家認為這個格是由兩條基本線構成的:一條垂直線和一條長度相等的水平線。想象一下在一張紙的中心畫一個點,畫一系列垂直或水平線,所有線都等長,從中心向外延伸,並標記線鏈末端的點。如果您對所有可能的鏈重複這些步驟,這些點將形成一個正方形網格。不同的初始線集建立不同的格。這兩條線的長度可能不相等,或者它們可能不是完全水平或垂直的,而是可以傾斜一定的角度。繪製此類線的鏈仍然會產生重複的點模式,但行和列會偏移或高度不同。
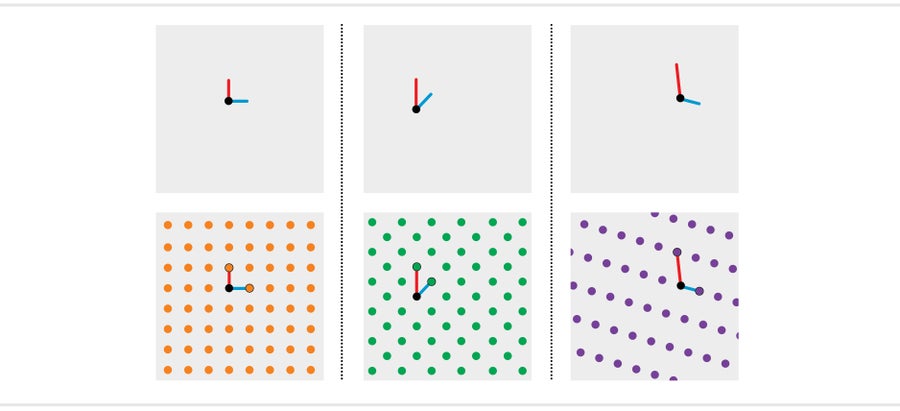
圖片來源:Jen Christiansen
格是一些看似棘手的數學問題的背景。假設我在一張紙上畫兩條線,並告訴您它們是格的構建塊。然後我在頁面上的某個地方畫一個點。您能找到最接近該點的格點嗎?
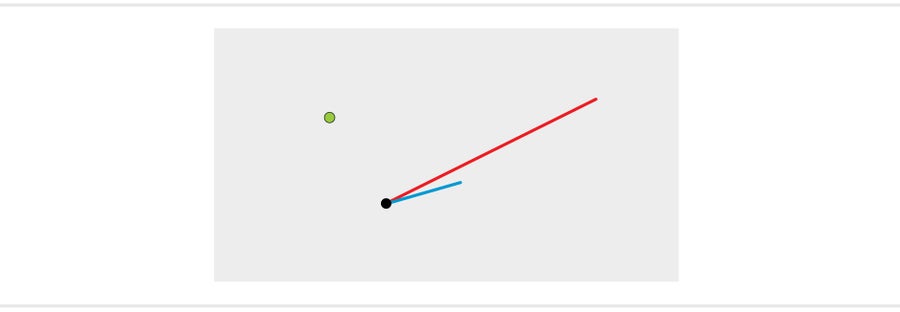
圖片來源:Jen Christiansen
您可能可以使用基本線開始繪製格點,並最終找到最接近的點。但這隻有在紙上的格是二維的情況下才有可能。我們的視覺想象力通常僅限於三維,但數學家可以描述數百維的格。在這些維度中,很難找到最近的格點。
研究人員使用這種巨大的格來構建密碼系統。例如,從一個 1,000 維的格開始。從這片點海中,選擇一個點。這個點的精確位置代表秘密訊息。然後在這個點附近稍微晃動一下,漂離格進入周圍空間。您可以公開共享新位置,而無需洩露秘密點的位置——找到附近的格點是一個非常難解的數學問題。就像混合成分保護布朗尼食譜一樣,晃動遠離秘密點會模糊其精確位置。
計算機科學家已經研究這些問題數十年,並且相當確信它們非常難以解決。但在設計新演算法時,密碼學家需要在安全性與許多其他考慮因素之間取得平衡,例如兩臺計算機需要交換的資訊量以及加密和解密訊息所需的計算難度。在這方面,基於格的密碼學表現出色。“格符合這個適中的位置,一切都合理——沒有太糟糕的,也沒有太好的,”佩克特說。“這有點像金髮姑娘。”
問題是,沒有人能保證基於格的密碼學永遠安全。為了防止數學突破解決底層問題——並破解程式碼——密碼學家需要訪問各種演算法型別。但 NIST 流程中四個最終候選演算法中有三個是基於格的演算法。在通用公鑰加密類別中選擇標準化的唯一演算法是 CRYSTALS-Kyber。

為了保護其脆弱的量子行為,量子計算機必須與其環境隔離並進行超冷冷卻。懸掛裝置使計算機(封裝在底部的隔間中)能夠冷卻。圖片來源:克里斯托弗·佩恩/Esto
NIST 競賽還設有數字簽名演算法類別,該類別提供有關誰傳送了訊息以及訊息未被修改的保證。加密演算法回答了“我知道沒有人會閱讀這個嗎?”這個問題,加利福尼亞州蒙特雷海軍研究生院的密碼學家布里塔·黑爾解釋說,而數字簽名回答了“我可以相信這些資料沒有被修改嗎?”這個問題。目前使用的數字簽名演算法也容易受到肖爾演算法的攻擊。NIST 選擇標準化三種數字簽名演算法,其中兩種是基於格的演算法。
如此嚴重地依賴單一型別的數學問題是有風險的。沒有人能確定數學家最終不會破解它。它也沒有給使用者任何靈活性——可能會發現另一種型別的密碼學更適合他們的特定需求。出於這些原因,NIST 擴充套件了這兩個類別的標準化過程,以研究非基於格的演算法。“我們的目標不是依賴任何一個數學族來選擇演算法,”NIST 的數學家達斯汀·穆迪解釋說。
即使是已經選擇標準化的演算法也需要在過程中進行調整。在第一輪提交後,研究人員注意到 CRYSTALS-Kyber 存在一個小問題,作者解決了這個問題。在競賽的後期,他們找到了一種稍微改進演算法的方法。“我們更改了引數以獲得更多的安全位元,”德國波鴻馬克斯·普朗克安全與隱私研究所的彼得·施瓦布說,他是 CRYSTALS-Kyber 的建立者之一。
NIST 現在正處於制定標準的階段,標準詳細描述了計算機程式設計師應如何逐步實施演算法。“網際網路上的一切都必須有非常具體、非常枯燥的標準,包含每一個小細節。否則計算機就無法相互通訊,”柳巴舍夫斯基說。標準制定後,每個計算機系統都需要切換到後量子密碼學。不會有所有人同時撥動開關的那一刻。各個軟體公司需要升級他們的協議,政府需要更改他們的要求,物理硬體裝置需要更換。
完全過渡到後量子密碼學可能需要很多年,甚至幾十年。在此之前,使用舊形式密碼學傳送的任何訊息都可能被未來的量子計算機讀取。根據您希望保守秘密的時間長短,擔憂的時間可能已經過去。正如黑爾所說,“在密碼學方面,每個人都在看錶,說,‘你們已經過期了。’”

