有時你的直覺會誤導你——尤其是在數學中,你經常會遇到看似不可能的結果。例如,無窮大並非總是等於無窮大,而烏龜可能超越人類運動員——至少從某種數學角度來看是這樣。
還有許多乍一看(或第二眼或第三眼)似乎自相矛盾的情況。然而,這些悖論是可以解釋的。它們不是錯誤,而是提醒我們不應在數學中過分依賴直覺。以下是該領域中最奇怪的三個悖論。
希爾伯特旅館
支援科學新聞報道
如果您喜歡這篇文章,請考慮訂閱以支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您將幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事能夠擁有未來。
想象一下,您正在前往一個城市旅行,卻忘記提前預訂房間。幸運的是,您偶然發現一家以著名數學家大衛·希爾伯特命名的美麗酒店,您非常欣賞他的工作。您走到接待處,看到這家酒店有無限數量的房間:房間號對應於自然數 1、2、3、4,...,永無止境。
然而,接待員告訴您酒店已滿。但您精通數學,所以不會輕易被敷衍了事。您知道一個技巧,可以讓您以及所有其他無數的客人也找到房間。您向接待員建議,讓每位客人搬到房間號比他們當前住宿房間號大一號的房間。因此,1 號房間的人搬到 2 號房間,2 號房間的人搬到 3 號房間,依此類推。
因為希爾伯特旅館擁有無限數量的可用房間,即使客滿,仍然有空間容納更多客人。而且這不僅僅適用於一個人:他們可以帶一整車也想要房間的人。在這種情況下,酒店客人必須搬到房間號不止大一號的房間。
更奇怪的是。即使您帶無限數量的人來到希爾伯特旅館,您仍然可以在客滿的酒店中容納他們。為此,1 號房間的客人必須搬到 2 號房間,2 號房間的客人搬到 4 號房間,3 號房間的客人搬到 6 號房間,依此類推。當每個人都搬到房間號是他們當前房間號兩倍的房間時,無限數量的奇數房間就空出來了。
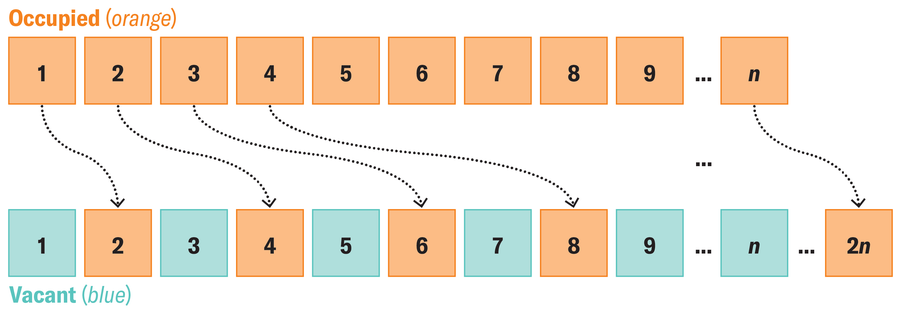
透過將每位客人移到房間號是他們當前房間號兩倍的房間中,就有空間容納無限數量的額外人員。
Jan Beránek/維基共享資源 (CC BY-SA 4.0),由阿曼達·蒙塔內斯重新設計
德國數學家大衛·希爾伯特在 1925 年關於無窮大的講座中提出了這個所謂的悖論。這個例子說明了並非所有概念都可以從有限情況轉移到無限情況:“每個房間都住滿了”和“酒店不能再接待更多客人”這兩個陳述在現實世界中是同義的——但在一個擁有無窮大的世界中則不然。
生日悖論
下一個悖論對許多人來說更熟悉。當我在學校時,我的幾個同學在同一天過生日的情況並不少見。事實上,我也和一個同學同一天生日。乍一看,這似乎是一個巨大的巧合。畢竟,一年有 365 天(閏年有 366 天,但為了簡單起見,我們忽略這一點),一個班級大約有 20 到 30 名學生。因此,我們的直覺告訴我們,兩個孩子在同一天出生的可能性不大。
但事實並非如此。事實上,在 23 人一組中,有兩人在同一天過生日的機率超過 50%。為了更好地理解這一點,最好不要看人數,而是看人與人之間的對數。從 23 個人中,可以形成 (23 x 22) / 2 = 253 對——這個數字超過了一年中天數的一半。如果我們看一下一個 23 人的班級中,有一個學生在特定日期出生的機率,那麼這個機率只有 1- ((365-1) /365)^23=6.1%。
因此,生日悖論的產生是由於檢視學生對會比只看個人給出更多的可能性。
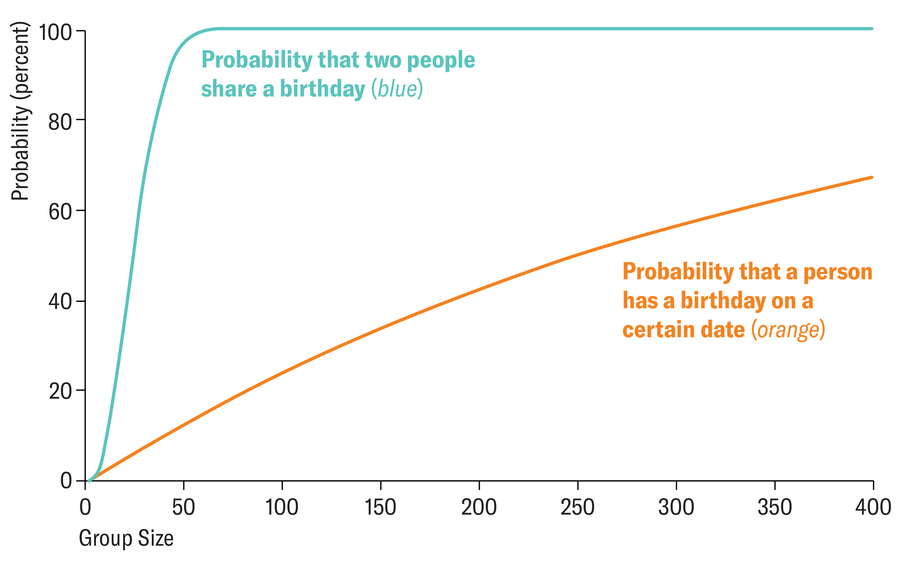
藍線表示一組人(x 軸上標明瞭組的大小)中有兩人生日相同的機率。橙線對應於一個人在特定日期過生日的機率。
Toobaz/維基共享資源 (CC BY-SA 4.0),由阿曼達·蒙塔內斯重新設計
這個事實在密碼學中具有實際效果。例如,如果您想簽署一份數字合同,則會使用“雜湊函式”:當文件被簽署時,它會被轉換為固定長度的字串(“雜湊”)。即使對原始文件進行最小的更改,從中形成的雜湊也會完全不同。透過保留他們的雜湊,簽名者可以證明他們最初簽署的內容——使該過程具有防篡改性。然而,兩個完全不同的文件會生成同一個雜湊的可能性極低,這會帶來安全風險。
通常,雜湊函式的長度被選擇為使得這種“衝突”(兩個不同的資料記錄產生相同的雜湊)極為罕見。然而,駭客可以進行“生日攻擊”:他們可以生成許多不同的文件,並將它們的雜湊函式成對比較——就像老師比較同學的生日而不是關注特定日期和單個學生一樣。
在實踐中,生日攻擊可能是這樣的:我首先建立兩個合同,V1 和 V2。V1 是一份公平的合同,但 V2 的措辭對我有好處。然後我在兩個合同的各個地方進行更改:我新增空格、製表符和換行符以建立 V1 和 V2 的變體。這些更改對於讀者來說幾乎是不可見的,但它們會徹底改變文件的雜湊函式。
如果我成對比較修改後的合同 V1 和 V2 的各個雜湊函式,我會比專門嘗試重現特定雜湊(例如 V1 的雜湊)更快地找到匹配的雜湊。如果我找到一對匹配的 V′1 和 V′2,我可以給您合同 V′1 簽名,但在事後聲稱您簽署了 V′2。因為兩者生成相同的雜湊,所以數字簽名軟體無法檢測到欺詐行為。
羅素悖論
英國哲學家伯特蘭·羅素在 1901 年提出了一個悖論,有時稱為羅素悖論——一個描述兩個看似矛盾的想法的術語。與希爾伯特旅館和生日悖論不同,羅素悖論不僅僅是一個逃脫我們直覺的結果。它本身就違反了邏輯規則。該悖論產生既非假亦非真的陳述。
有幾個例子可以說明羅素悖論,但一個著名的例子是“理髮師悖論”。假設一位理髮師為鎮上所有不給自己刮鬍子的人刮鬍子——並且只為這些人刮鬍子。理髮師給自己刮鬍子嗎?如果他給自己刮鬍子,那麼他就不再屬於不給自己刮鬍子的人群。但如果他不給自己刮鬍子,那麼根據定義,他就必須給自己刮鬍子(因為所有不給自己刮鬍子的居民都會去找他)。
這個問題是由於集合定義不明確而引起的。在羅素提出悖論的時候,集合通常指的是事物的集合:例如,自然數形成一個集合,所有不給自己刮鬍子的居民的集合也是如此。這也允許集合包含自身或將自身作為一個整體來引用——而這些屬性會導致矛盾。因此,這個悖論導致了數學家所稱的“樸素集合論”的終結。
數學的基礎仍然依賴於集合論。但是,這種結構中的集合不再僅僅是集合,而必須滿足某些條件。例如,集合必須由已存在的集合組成,並且不得引用自身。這排除了諸如理髮師悖論之類的悖論。
用數學符號表示:鎮上可以長鬍須的男性構成集合 M。該集合包括給自己刮鬍子的男性和不給自己刮鬍子的男性。接下來,集合 C 包括理髮師的所有顧客。要形成 C,您必須遵循現代集合論的規則:如果理髮師是一個有鬍鬚的男人,或者 M 的一部分,那麼顧客集合就不能定義為“所有不給自己刮鬍子的男性居民”——因為在這種情況下,定義會引用自身,理髮師和顧客都是 M 的一部分。集合論根本不允許這樣的定義。但是,如果理髮師不是 M 的一部分——例如,如果理髮師是女性或無法長出鬍鬚——那麼這個定義是被允許的。
我們現在可以鬆一口氣了:悖論已經解決,數學並沒有註定失敗。然而,不能保證數學規則在某個時候不會產生無法解決的矛盾。邏輯學家庫爾特·哥德爾在 20 世紀 30 年代證明了這一點——並且這樣做清楚地表明,不能確定數學將永遠以自洽的方式運作。我們能做的最好的事情是希望永遠不會出現無法解決的矛盾。
本文最初發表在《科學世界》雜誌上,經許可轉載。
