你能想象到的最奇異的實數是什麼?可能很多人會想到像 pi (π) 或尤拉數這樣的無理數。事實上,這些值可以被認為是“狂野的”。畢竟,它們的十進位制表示是無限的,沒有數字會重複。然而,即使是這些看起來很瘋狂的數字,連同所有有理數,也僅佔實數(或可以出現在數軸上的數字)的一小部分。(提醒一下,這些是可以用於各種常見測量的數字型別,包括時間、溫度和距離。)
但事實證明,如果你碰巧在數軸上隨機選擇一個數字,你幾乎肯定會抽到一個“不可計算”的數字。對於這樣的值,沒有辦法精確地確定它們。
實數由有理數和無理陣列成。有理數(即可寫成p⁄q分數的數,其中p和q是整數)包括自然數(0、1、2、3...)和整數(...、–2、–1、0、1、2...)。數軸上的其餘數字是無理數。這些數字也可以分為不同的類別——其中大多數是我們甚至無法想象的。
支援科學新聞業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞業 訂閱。透過購買訂閱,您正在幫助確保關於塑造我們今天世界的發現和想法的具有影響力的故事的未來。
無窮大、無窮小、虛數或其他不尋常的數字空間可能難以描述,這似乎並不太令人驚訝。但人們會認為我們現在可以完全理解描述我們世界中距離的實數。不幸的是,事情並非那麼簡單。要理解這一點,我們必須仔細研究無理數。
什麼是無理數?
所有不能表示為兩個整數之比的實數都是無理數。(提醒:整數是整數。)無理數包括,例如,2 的平方根,其十進位制表示是無限的,且永不重複。事實上,√2 是最簡單的無理數之一,因為它是可構造的——也就是說,它可以透過使用圓規和直尺繪製兩條邊長為 1 個單位的直角三角形來生成。那麼該三角形的斜邊長度為 √2。以類似的方式,黃金比例 φ 可以幾何構造,許多其他無理數值也可以。
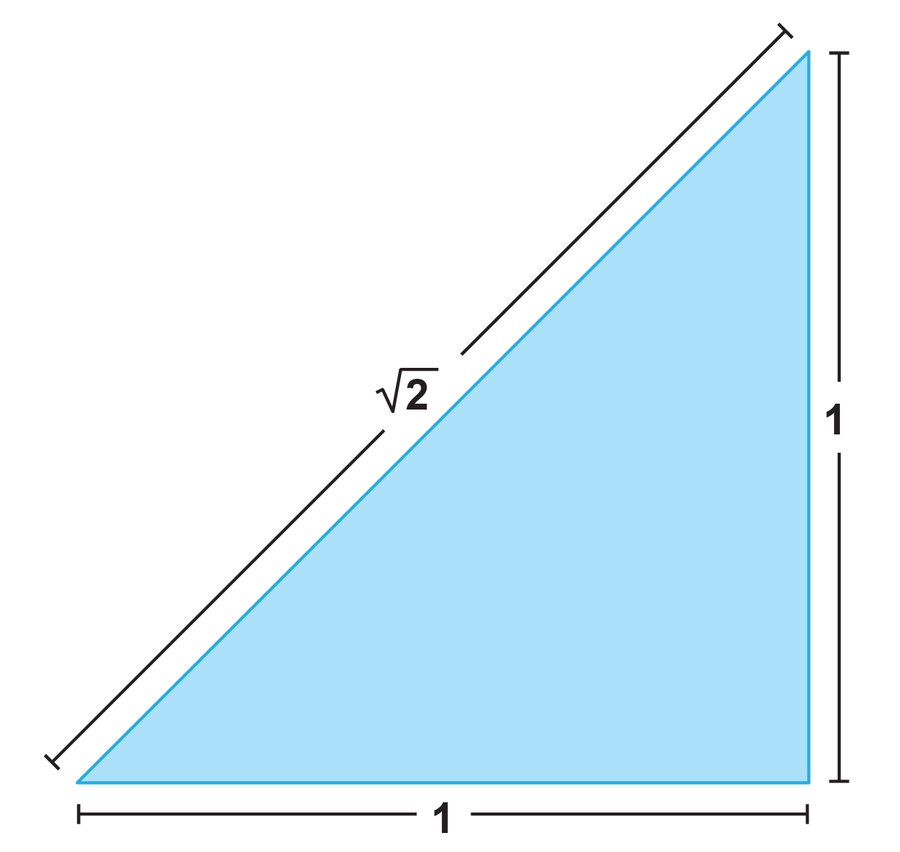
透過建立一個兩條邊長為 1 的直角三角形,可以幾何構造 2 的平方根。剩餘邊的長度將為 2 的平方根。圖片來源:Rubber Duck/ Pbroks13/Wikimedia Commons,由大眾科學設計
然而,即使在古代,人們也遇到了無法以如此簡單的幾何方式生成的數字。一個著名的例子是立方倍積問題:如何將邊長為 1 的立方體構造為體積是其兩倍的立方體?正如數學家皮埃爾·萬策爾在 1837 年發現的那樣,這個新立方體所需的邊長 ∛2 無法使用圓規和直尺構造。但是 ∛2 屬於代數數,它可以寫成多項式方程的解。對於 ∛2,相應的方程是 x3 = 2。
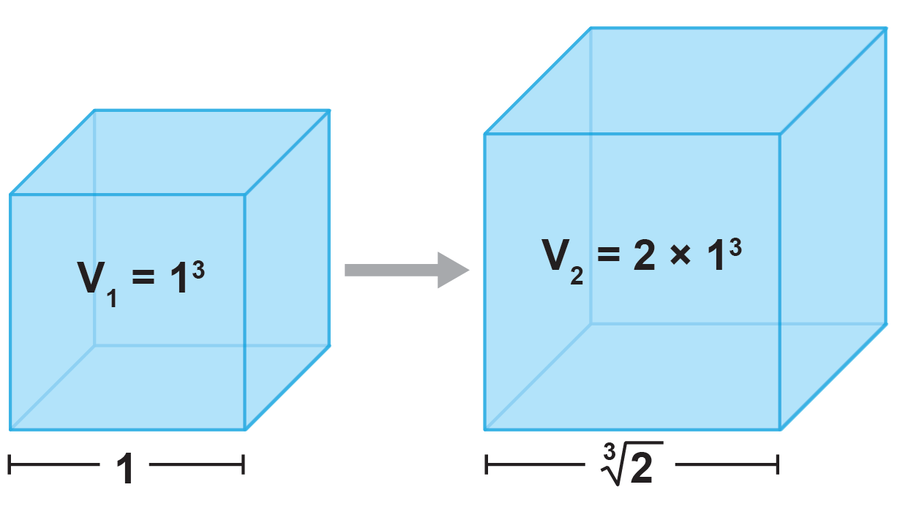
有些無理數無法通過幾何方式構造。例如,一個邊長為 1 的立方體,如果不使用多項式方程(即 2 的立方根)來表示體積,就無法將體積翻倍。圖片來源:Petrus3743/Wikimedia Commons (CC BY-SA 4.0),由大眾科學設計
有些數字是超越數
還有一些超越數,它們不能表示為這種方程的解。也就是說,沒有簡單的公式可以計算它們。著名的 π 就屬於這一類。但這並不意味著我們不知道它的值。希臘數學家阿基米德發現了一個計算規則來確定 π,至少是近似值。此外,還有許多演算法可以隨意吐出 π 的第 5.87 億位小數。在足夠的計算能力和時間下,至少在理論上,這個數字可以被確定到任意精度。尤拉數 (e) 或 2√2 也同樣適用。
超越數蘊藏著許多謎團。雖然有明確的方法來判斷一個數是否是可構造的,但相比之下,證明一個值是否是超越數卻很困難。例如,在 1934 年,蘇聯數學家亞歷山大·蓋爾豐德成功證明複合數 eπ 是超越數。但是,πe 或 π x e 或 π – e 的值是代數數還是超越數,至今仍不清楚。
不可計算數更加奇怪
直到 20 世紀初,人們還認為超越數是實數所能提供的最瘋狂的東西。但這是錯誤的。1937 年,英國數學家艾倫·圖靈發表了一篇關於可計算數的論文。他用這個術語來描述所有那些存在計算規則(即演算法)的值,計算機可以執行該規則來計算任意精度的數值。
幾乎所有已知的超越數,例如 π 和 e,都屬於這一類。畢竟,我們至少知道它們的近似數值,以及如何計算它們。然而,正如圖靈在他的工作中表明的那樣,也存在同樣不可計算的數字,其值無法以任意精度逼近——也就是說,我們不知道它們是什麼樣子。
更糟糕的是:幾乎所有實數都是不可計算的。
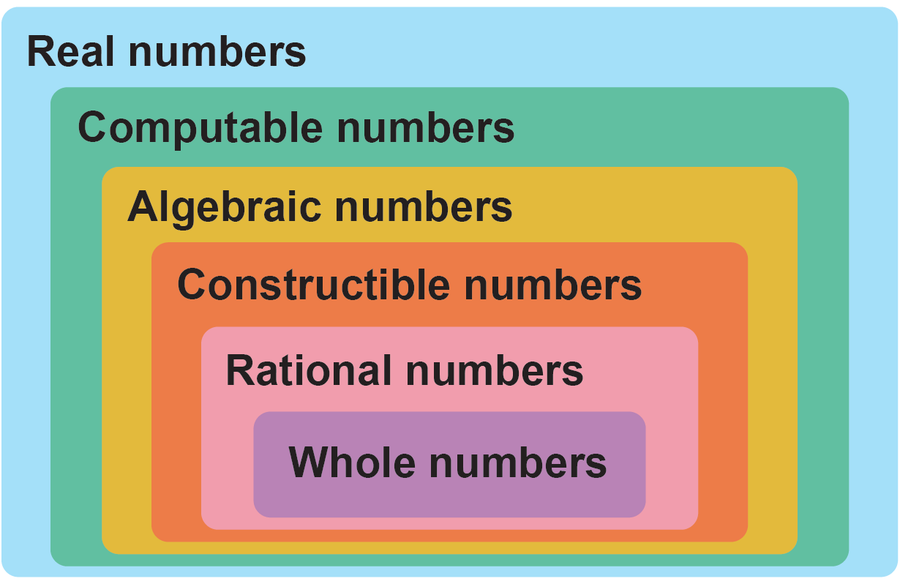
實數包括可計算數、代數數、可構造數、有理數和整數。圖片來源:Spektrum der Wissenschaft/馬農·比肖夫,由大眾科學設計
如果思考不同數集的無限大小,就會認識到這一點。數學家格奧爾格·康托爾在 19 世紀末為這個想法奠定了基礎。當時,他能夠證明,例如,自然數、整數和有理數的集合具有相同的基數(集合大小的數學表示式)。為什麼會這樣?要理解這一點,首先應該注意到,有限數的相同計算規則不適用於無窮大。以自然數和整數為例:可以將一個正整數和一個負整數交替分配給每個自然數,例如 (0, 0)、(1, –1)、(2, 1)、(3, –2)、(4, 2),等等。由於自然數沒有盡頭,因此我們找到了兩個集合之間的一一對映。這就像在公共汽車站為每個人分配一個座位,反之亦然。在這種情況下,我們知道公共汽車上的座位和公共汽車站的人數一樣多。自然數和整數也是如此。
在有理數和自然數之間可以找到類似的一一對映。正如康托爾能夠證明的那樣,自然數的基數是最小的可能無窮大。他稱之為“可數無限”。
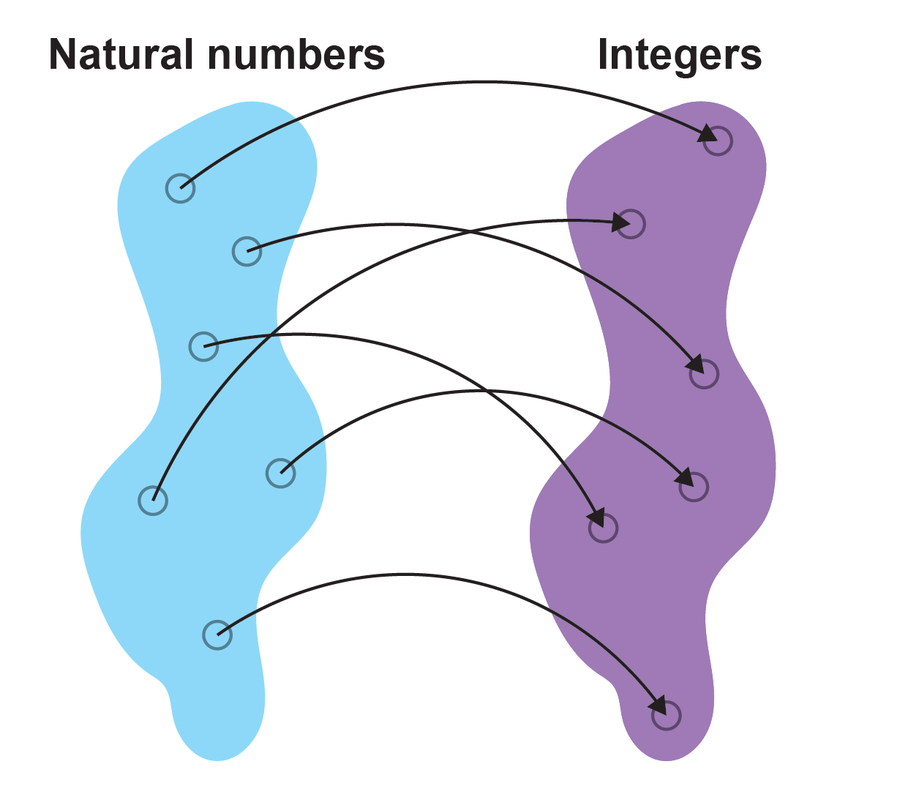
如果各個集合的元素之間存在一一對映,則兩個集合相等。圖片來源:Spektrum der Wissenschaft/馬農·比肖夫,由大眾科學設計
另一方面,實數是不可數的。康托爾能夠證明,實數的基數必然大於自然數的基數。他透過證明,無論列表有多長,都無法列舉所有實數而不遺漏某些值。因此,實數構成一個不可數集。
康托爾的推理如下:假設有一個包含所有實數的列表。那麼可以將此列表想象成一個表格。在每一行中,都有一個數字,每一列都為小數點位置提供一個位置。康托爾證明,如果在該表格中圍繞一組形成對角線的數字(例如,第一行中的第一位數字,第二行中的第二位數字等)畫一個圓圈,則可以透過將 1 新增到每個對角線條目來建立一個新的實數。這個新數字不能包含在列表中。因此,您最初的所有實數列表是不完整的。
但是正如圖靈所說,所有可計算數都必須是可數的。對於這些數字中的每一個,都可以開發一臺機器,該機器只需計算其值即可。由於可以對這些計算機器進行編號,因此可計算數必然是可數的。反過來,這導致不可計算數在絕大多數實數中占主導地位:它們的數量是不可數的!
因此,如果你計算隨機抽取一個實數時會遇到哪種實數的機率,你將得到一個明確的結果:在 100% 的情況下,這個數字將是不可計算的。但這並不意味著你不能抽取任何其他數字。對於無限組事件,機率為零並不意味著結果是不可能的。
考慮到我們知道的可計算數的豐富性,不可計算數如此豐富這一事實更加令人驚訝,
停機問題作為靈感
少數現有的不可計算數示例是由計算機科學中著名的停機問題定義的。要思考這個問題(由圖靈提出),請想象一臺計算機執行一組特定的指令以解決問題(換句話說,計算機正在使用演算法)。在停機問題中,要求您想象一臺機器,它可以判斷執行給定演算法的計算機是否會在某個時候停止,還是會永遠繼續下去。正如圖靈所證明的那樣,雖然這樣一臺機器可以判斷某些演算法是否可以在有限時間內執行,但顯然沒有一種方法可以對所有可能的程式程式碼執行此操作。停機問題是數學家的直接應用
庫爾特·哥德爾不完備性定理,該定理指出並非所有數學陳述都可以證明。
阿根廷裔美國數學家格雷戈裡·柴廷使用停機問題來定義不可計算數。所謂的柴廷常數 Ω 對應於計算機的理論模型(圖靈機)對於任何給定輸入停止的機率:Ω = –∑p½|p|,其中 p 表示所有在有限執行時後停止的程式,|p| 描述了程式的長度,單位為位元。
因此,要精確計算柴廷常數,就需要知道哪些程式停止,哪些程式不停止,根據停機問題,這是不可能的。儘管如此,在 2000 年,數學家克里斯蒂安·S·卡盧德和他的同事成功地計算出了柴廷常數的前幾位數字:0.0157499939956247687....
這意味著,如果你在卡盧德及其同事使用的語言中隨機生成一個程式,它將以大約 1.58% 的機率在有限的執行時間內停止。即使結果具有很高的精度,柴廷常數也無法以任意精度計算。
一個不可計算數和一隻忙碌的海狸
另一個不可計算數來自“忙碌的海狸函式”,或 BB(n)。此函式計算演算法可以從 n 位產生的最大可能輸出(以位元為單位測量)。
例如,不可計算數來自以下構造:∑n½BB(n)。到目前為止,只知道忙碌的海狸函式的前四個值。至少可以估計另外兩個值。
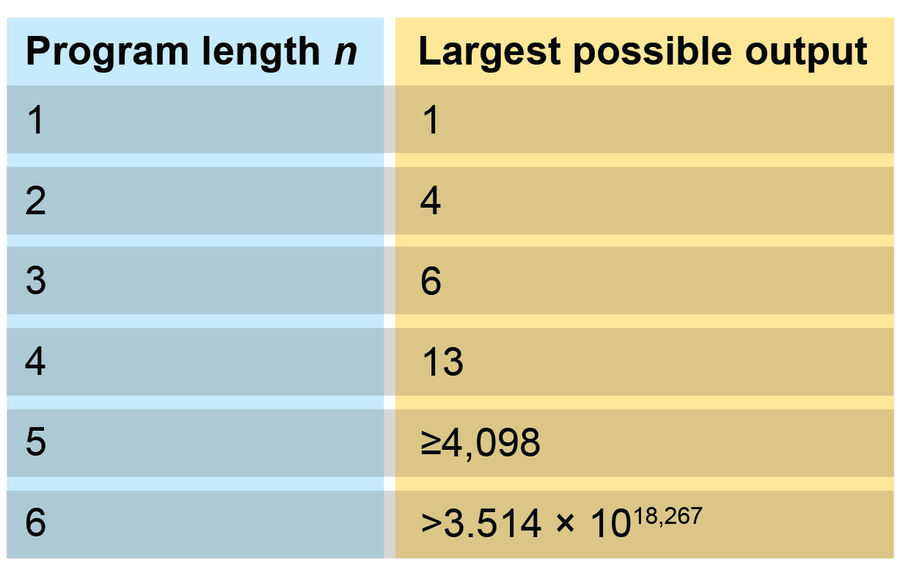
忙碌的海狸函式計算演算法可以從給定數量 (n) 的位元產生的最大可能輸出(以位元為單位測量)。圖片來源:Spektrum der Wissenschaft/馬農·比肖夫,由大眾科學設計
因此,這個不可計算數的前幾位數字是 ∑n½BB(n) = 0.51562548....
還有其他複雜的方法可以定義不可計算數。也許你也可以想出一個變體。儘管如此,鑑於我們知道的可計算數的豐富性,不可計算值主導實數——從而主導我們的世界,這始終令人驚訝。
本文最初發表在《Spektrum der Wissenschaft》雜誌上,並經許可轉載。
編者注(2023 年 6 月 13 日):本文在釋出後進行了編輯,以更正忙碌的海狸函式的圖形以及關於隨機生成卡盧德及其同事使用的語言的程式時會發生什麼情況的描述。