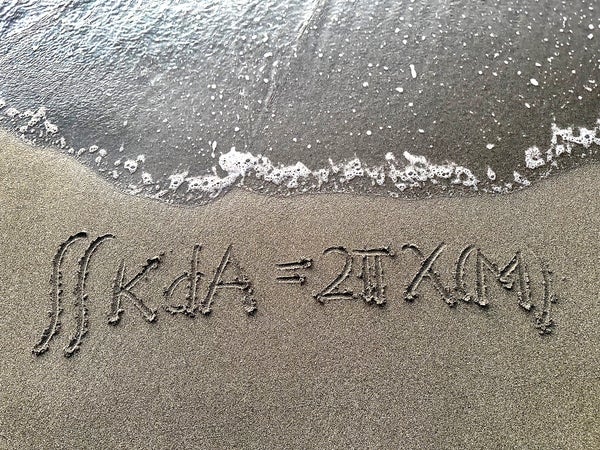對於數學家來說,方程就是藝術。正如許多人會被繪畫或音樂所感動一樣,對於那些欣賞和理解數學的人來說,數字、變數、運算以及量與量之間關係的表達也同樣引人入勝。
正如藝術美一樣,數學美也存在於觀察者的眼中。一位數學家可能會珍視簡單明瞭、簡潔的方程,而另一位數學家可能更喜歡相反的方程。正如有些人喜歡現代藝術,而另一些人則喜歡中世紀作品一樣,古代和現代的方程都因其巧妙、強大和可能性而受到讚賞。
以下是一些數學家選擇的最美麗的數學方程,以及他們自己關於哪些因素使它們如此精美的看法。
關於支援科學新聞業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞業 訂閱。透過購買訂閱,您正在幫助確保關於塑造我們今天世界的發現和想法的具有影響力的故事的未來。
洛伊納微分方程
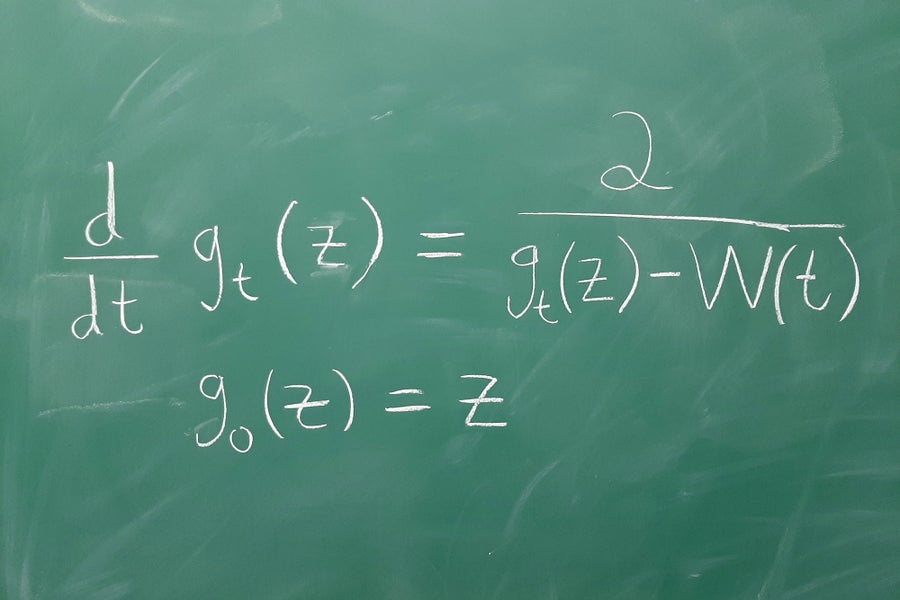
尤恩·格溫
有些方程之所以美麗,是因為它們揭示了不同學科之間意想不到的關係。洛伊納微分方程由查爾斯·洛伊納於 1923 年提出,描述了定義在複平面子集上的一系列共形(保角)函式的時間演化。該方程的輸入是一個連續函式 W(t),稱為驅動函式。
近 80 年後的 1999 年,奧德·施拉姆發現,當驅動函式被視為布朗運動(機率論研究的中心物件)時,洛伊納方程的解具有特殊的對稱性。在施拉姆的發現基礎上,證明了對於驅動函式的這種選擇,洛伊納方程的解,稱為施拉姆-洛伊納演化,描述了二維統計力學中各種臨界模型的大尺度行為。在施拉姆的工作之前,洛伊納方程在機率論中的這種應用是完全出乎意料的。它徹底改變了統計力學的數學研究,並導致了過去二十年數學領域一些最激動人心的突破。——尤恩·格溫,芝加哥大學
高斯-博內方程
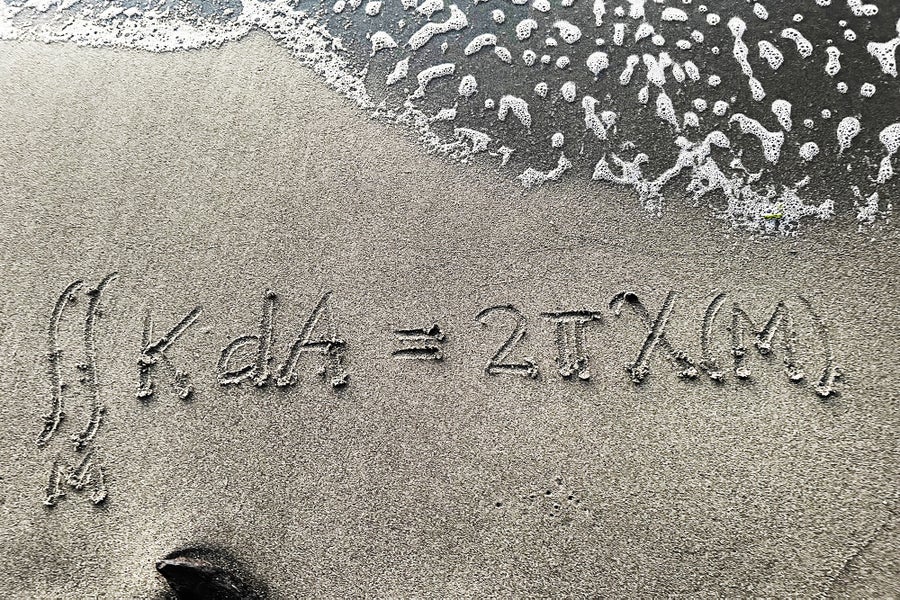
艾拉娜·弗雷澤
高斯-博內公式是微分幾何中一個美麗的方程,它斷言曲面上高斯曲率的積分等於一個常數乘以曲面的尤拉示性數。這個方程之所以引人注目,是因為它將兩個非常不同的量聯絡起來:一方面是曲面的曲率,另一方面是曲面的拓撲結構。曲面上一點的曲率是該點曲面彎曲程度的度量,或者曲面偏離平面的程度。尤拉示性數是曲面的全域性拓撲不變數,它描述了曲面的拓撲結構,而與其彎曲方式無關。這個方程令人驚訝,例如,它意味著如果您連續地變形一個曲面,總曲率將保持不變。高斯-博內方程的各種版本最初由卡爾·弗里德里希·高斯和皮埃爾·奧西恩·博內於 19 世紀上半葉提出,它仍然是幾何學中最美麗和最引人注目的方程之一。這個方程的一些美麗之處在於其表示式的簡潔性和它所表達的深刻性。 ——艾拉娜·弗雷澤,不列顛哥倫比亞大學
索博列夫不等式
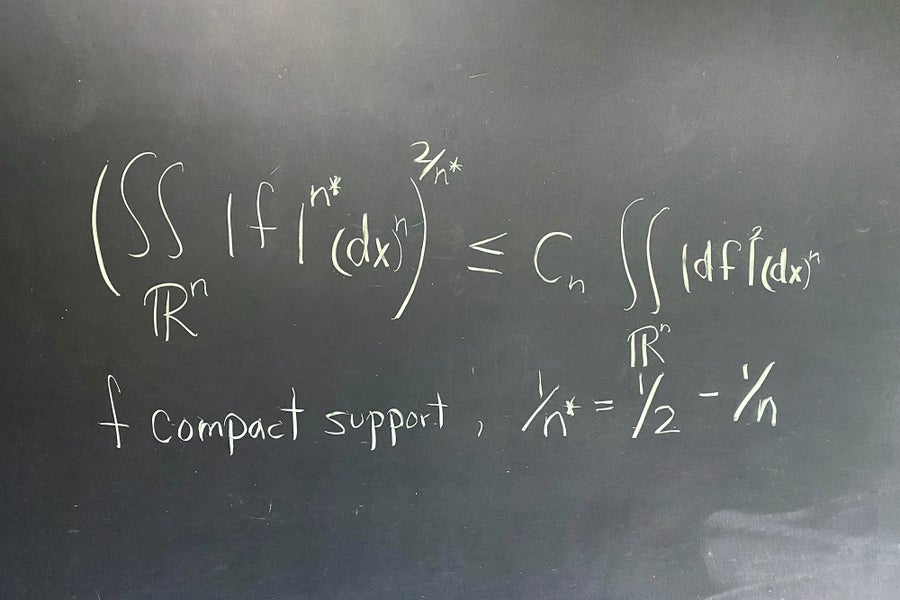
凱倫·烏倫貝克
我喜歡不等式。索博列夫不等式和相關不等式估計了導數項中的函式,構成了我們理解偏微分方程的基礎。當 n = 2 時不等式的失敗與 n = 2 特有的性質有關。——凱倫·烏倫貝克,普林斯頓高等研究院
黎曼-羅赫等式
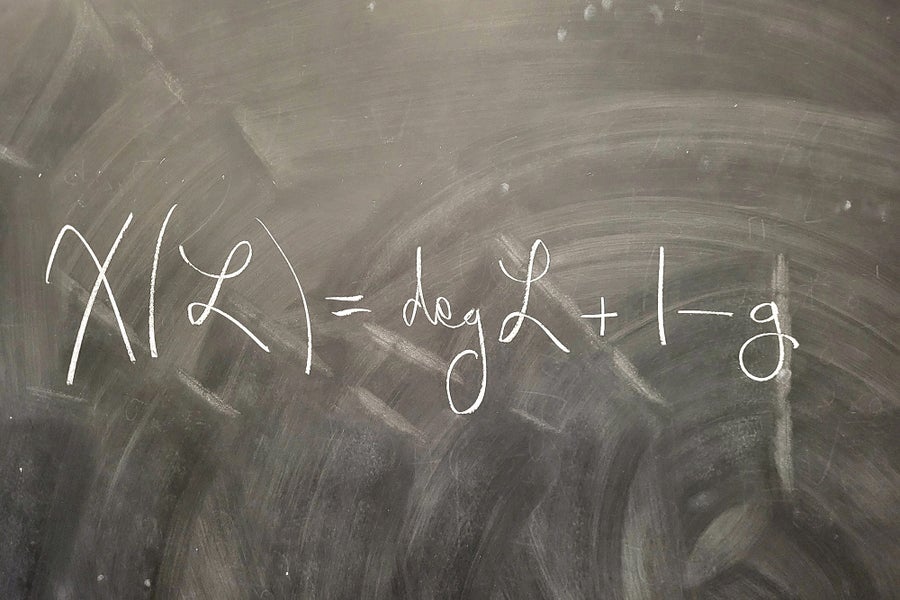
桑多爾·科瓦奇
黎曼曲面是一個緊緻可定向曲面。黎曼曲面的區別在於它們容納的孔或把手的數量。這個數字稱為虧格,用 g 表示。例如,虧格 g=0 的黎曼曲面是一個球面,虧格 g=1 的黎曼曲面是一個環面,或甜甜圈。復黎曼曲面是一個具有復結構的黎曼曲面。換句話說,它也是一個複流形。
黎曼曲面上的除子是有限多個點的選擇。除子的次數是其中點的數量。它用“deg”表示。先驗地,除子僅僅取決於拓撲資訊,除子的次數也是如此。然而,一旦黎曼曲面配備了復結構——換句話說,當它被視為複流形時——那麼人們可能會問關於該復結構的問題,例如是否存在亞純函式,其零點或極點與給定的除子一致。這引出了經典米塔-列夫勒問題的一個版本。由復結構確定的最簡單的不變數之一是除子的全純尤拉示性數,它在某種程度上是該特定黎曼曲面上米塔-列夫勒問題的校正項。對於除子 ℒ,其全純尤拉示性數用 χ(ℒ) 表示。
現在我們準備陳述黎曼-羅赫等式。考慮虧格為 g 的復黎曼曲面以及其上的除子 ℒ。該方程為 χ(ℒ) = degℒ + 1 – g。
這個看似簡單的方程具有深遠的意義。除其他外,它意味著全純尤拉示性數僅取決於拓撲資訊。
至於是什麼使一個方程變得美麗,我想說,我發現那些要麼揭示意想不到的東西,要麼連線看似無關的不變數的方程很有趣。——桑多爾·科瓦奇,華盛頓大學
分次環之間的同構

大衛·阿亞拉
我發現這個方程很美,因為它新穎且令人驚訝,並且資訊顯然從右側項 (RHT) 流向左側項 (LHT)。事實上,LHT 顯然是幾何的,而 RHT 純粹是代數的。此外,由於 RHT 是可計算的,因此該方程給出了流形的分類,這是一項深入研究的企業。最後,這個結果是同類首創,其證明技術促使了數學許多領域中富有創造力的新方法和視角。——大衛·阿亞拉,蒙大拿州立大學
無窮級數
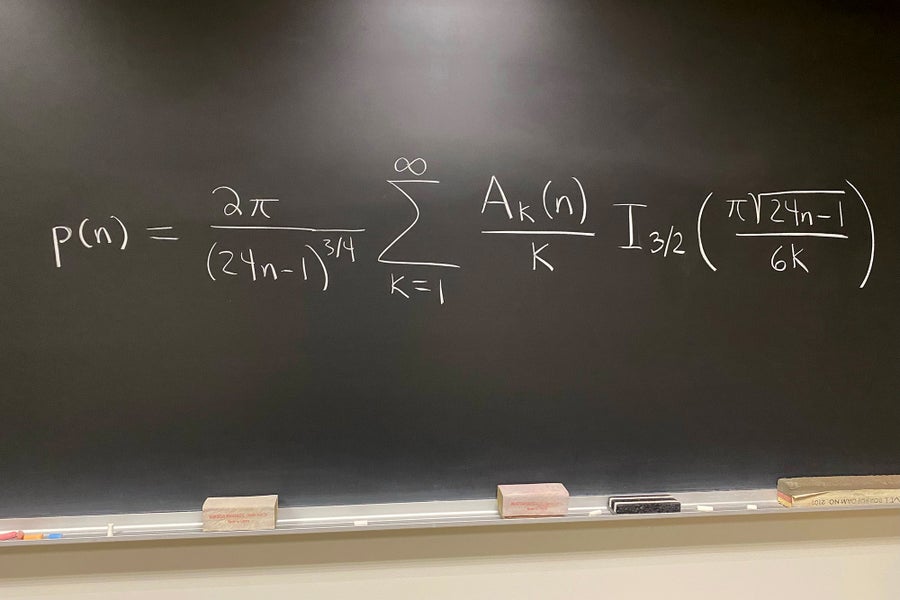
阿曼達·L·福爾瑟姆
我不認為存在一個最美麗的數學方程,但這個方程對我來說很突出。在撰寫這篇文章時,我向一個年幼的孩子展示了它的照片。我們首先討論了方程是什麼(一個用等號連線兩個事物的數學陳述,例如 4 = 2 + 1 + 1),他們問為什麼這個方程這麼大。我們討論了右側在視覺上是較大的一側,但左側不是——右側是一個和(如 2 + 1 + 1),但有無限多項,而左側與數論中的整數分拆有關。例如,n = 4 有五個分拆 (4, 3 + 1, 2 + 2, 2 + 1 + 1, 1 + 1 + 1 + 1),因此在 n = 4 處評估的分拆函式 p(n) 為 5 (p(4) = 5)。
這個重要且看似基本的功能與加法和計數有關,但它非常複雜,這也許是出乎意料的。例如,p(100) 超過 1.9 億,但可以肯定的是,找出答案的方法不是寫出 n = 100 的數百萬個分拆並計算有多少個。感謝漢斯·拉德馬赫在 1937 年的工作,他擴充套件了 G. H. 哈代和斯里尼瓦薩·拉馬努金的早期相關工作,這個方程的右側是 p(n) 的精確公式。有些人可能會認為(大的)右側,一個涉及復(虛)數 (Ak(n))、分數冪(3/4 和平方根)、超越數 pi 等等的無限和,與美麗相反,或者令人望而生畏——特別是考慮到它取代了(視覺上很小的)左側,即使是孩子也能理解。解析數論以及拉德馬赫和哈代以及拉馬努金的工作的美麗之處在於,它表明 p(n) 的這個公式是存在的——這本身就是一項壯舉——並且事實證明,透過截斷無限和並進行四捨五入,它對於計算 p(n) 是實用的。這裡出現的無限和收斂,意味著它求和為有限值、一個計算重要事物的實數,並且不會不斷累積——更不用說數學遺產、進一步的研究以及與今天仍然存在的其他領域的聯絡,現在已經接近一個世紀了。——阿曼達·福爾瑟姆,阿默斯特學院
尤拉乘積公式
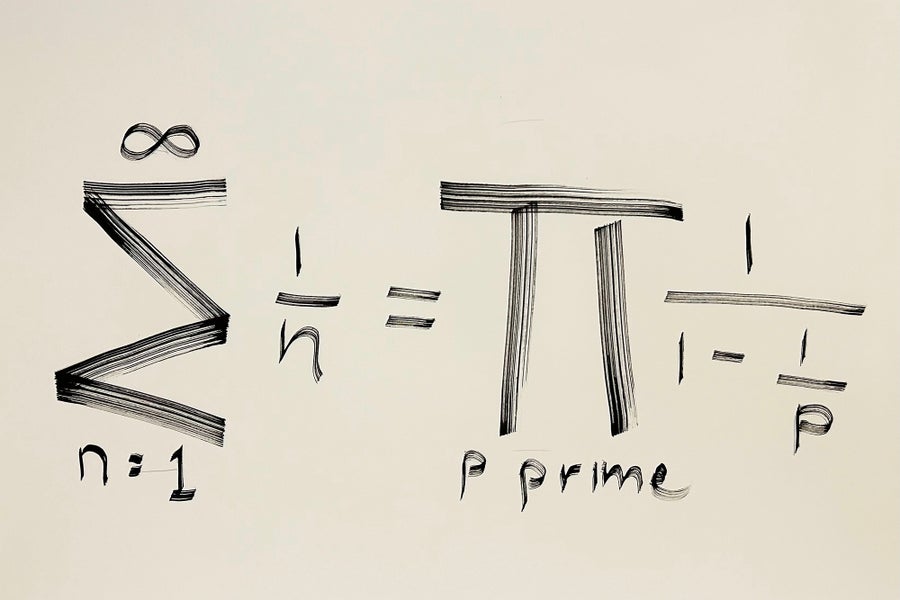
理查德·施瓦茨
很難挑選出數學中最美麗的單個方程,但我認為尤拉乘積公式在任何此類列表中都名列前茅。讓我讚揚一下這個公式的優點。首先,它很簡單。它只涉及加法、減法、乘法和除法運算。其次,它是基本的:它表達了左側計數數字和右側質數之間的深刻關係。第三,它令人驚訝且出乎意料,以一種非常新穎的方式將基本運算交織在一起。第四,它有用且功能強大。僅僅作為一個開始,它就給出了質數無窮性的另一種證明。左側是一個發散級數。如果只有有限多個質數,則右側將是有限的,這是一個矛盾。人們還可以從方程中擠出關於質數的更深層資訊。例如,人們可以使用尤拉乘積公式來證明質數倒數的和是發散的。這個結果遠遠超出了歐幾里得關於質數無窮性的經典證明。第五,該公式非常流行。它仍然在數論中發揮著重要作用,並且是理解質數分佈的關鍵工具之一,即使在今天也是如此。第六,它是可訪問的:它有一個優雅的證明,使用了整數可以唯一分解的事實,以及幾何級數的簡潔性質。——理查德·施瓦茨,布朗大學
賴芬貝格平坦集
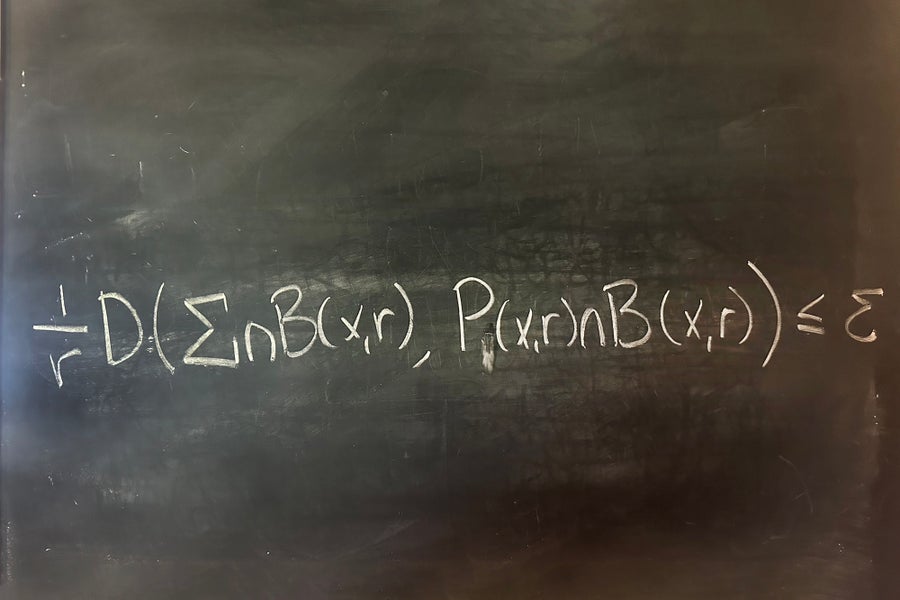
西爾維婭·吉納西
滿足圖片中不等式(它們是隱藏的,但有兩個!)的集合 Σ 稱為賴芬貝格平坦。與往常一樣,數學中的符號 ε 代表一個很小的量;我們基本上是在說,在每個球 B(x,r) 中,在每個尺度和位置,都存在一個平面 P(x,r),其與我們集合的距離非常小(εr)。
彼得·賴芬貝格在 1960 年證明,拓撲上,這些集合是圓盤。(這是一件好事:沒有撕裂、孔洞或奇怪的扭曲。)事實上,正如最近的結果表明,要求這些集合稍微額外平坦會導致更平滑的引數化。對於一個集合來說,平坦性要求很高,但它在正則性方面確實得到了回報。平坦性(幾何)和正則性(分析)之間的相互作用是我熱愛數學一切事物的核心,這也是大多數讀者已經知道但可能沒有意識到的:我們很早就知道導數給了我們切線!
我不認為數學之美在於方程,儘管我確信良好的筆跡可以創造奇蹟。我絕大多數時候在那些能夠將兩個數學宇宙結合在一起,為新概念創造空間,同時增強我們對舊概念的理解的想法中找到它。——西爾維婭·吉納西,華盛頓大學
(1/p) + (1/q) + (1/r) = 1
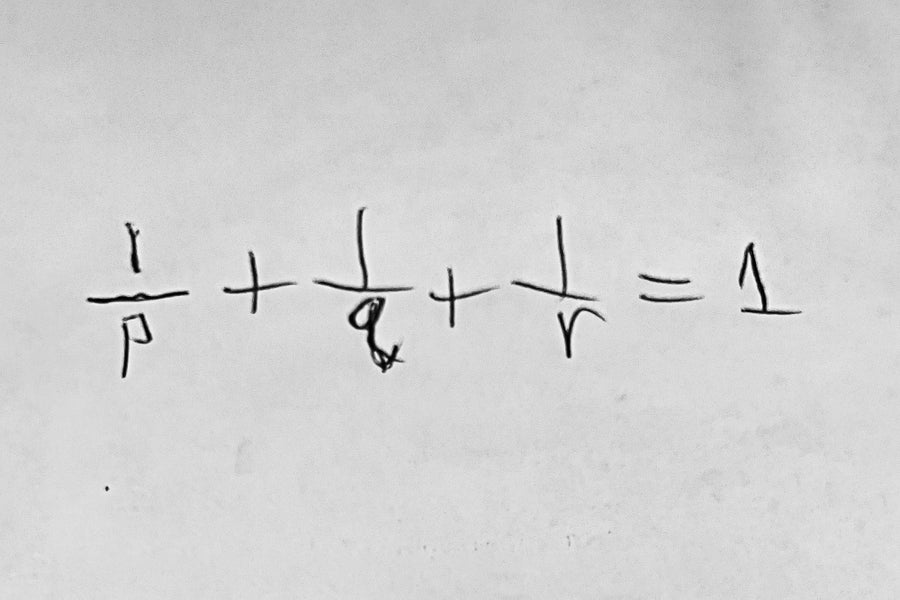
蒙蒂·麥戈文
我最喜歡的方程是 (1/p) + (1/q) + (1/r) = 1。它在正整數中唯一的解是 p = q = r = 3;p = 2, q = r = 4;和 p = 2, q = 3, r = 6。這個方程與一類稱為考克斯特群或反射群的美麗群有關,並標誌著這類群的有限群和無限群之間的關鍵邊界。它的解與僅有的幾種用正多邊形平鋪平面的方法密切相關,即用等邊三角形、正方形或六邊形平鋪平面。——蒙蒂·麥戈文,華盛頓大學