無法解決的問題

我們三人當時正坐在奧地利阿爾卑斯山深處小鎮塞費爾德的一家咖啡館裡。那是2012年的夏天，我們遇到了難題。並不是被困在咖啡館裡——陽光明媚，阿爾卑斯山上的積雪閃閃發光，美麗的景色非常誘人，我們差點就放棄了讓我們陷入困境的數學問題，跑到戶外去了。我們當時試圖探索庫爾特·哥德爾和艾倫·圖靈在20世紀取得的數學成果與量子物理學之間的聯絡。至少，那是我們的夢想。這個夢想始於2010年，當時我們在斯德哥爾摩附近的米塔格-萊夫勒研究所參加了一個為期一個學期的量子資訊專案。

我們研究的一些問題以前曾被其他人探索過，但對我們來說，這個研究方向是全新的，所以我們從一些簡單的事情開始。當時，我們正試圖證明一個很小且不太重要的結果，以便對事情有所瞭解。幾個月以來，我們已經有了這個結果的（某種）證明。但是為了使證明有效，我們不得不以一種人為的且令人不滿意的方式設定問題。感覺就像為了迎合答案而改變問題，我們對此很不滿意。在2012年將我們聚集在一起的塞費爾德研討會的第一次會談結束後，我們在休息期間再次研究這個問題，但仍然看不到任何解決問題的方法。我們中的一人（邁克爾·沃爾夫）半開玩笑地問：“我們為什麼不證明一些人們真正關心的事情的不可判定性，比如譜隙？”

當時，我們對物理學中的某些問題是否“可判定”或“不可判定”感興趣——也就是說，它們是否有可能被解決？我們陷入了困境，試圖探究一個更次要問題的可判定性，這個問題很少有人關心。“譜隙”問題是邁克爾建議我們解決的問題（我們稍後會解釋），它是物理學的核心問題之一。我們當時不知道這個問題是否可判定（儘管我們預感它不可判定），也不知道我們是否能夠證明任何一種情況。但是如果我們能做到，結果將對物理學具有真正的意義，更不用說這是一項重大的數學成就。邁克爾提出的雄心勃勃的建議，幾乎是開玩笑地提出的，開啟了我們一段宏大的冒險。三年後，在146頁的數學證明之後，我們關於譜隙不可判定性的證明發表在《自然》雜誌上。

關於支援科學新聞報道

如果您喜歡這篇文章，請考慮透過以下方式支援我們屢獲殊榮的新聞報道： 訂閱。透過購買訂閱，您正在幫助確保有關塑造我們當今世界的發現和想法的有影響力的故事的未來。

為了理解這意味著什麼，我們需要回到20世紀初，追溯一些孕育出現代物理學、數學和計算機科學的線索。這些不同的想法都指向德國數學家大衛·希爾伯特，他通常被認為是過去100年中該領域最偉大的人物。（當然，數學界以外的人沒有人聽說過他。數學學科不是通往名聲和名譽的好途徑，儘管它有自身的獎勵。）

量子力學的數學

希爾伯特對數學的影響是巨大的。早期，他發展了一個名為泛函分析的數學分支——特別是稱為譜理論的領域，這最終將成為我們證明中問題的關鍵。希爾伯特出於純粹抽象的原因對這個領域感興趣。但正如經常發生的那樣，他的數學結果最終恰好是理解當時困擾物理學家的問題所必需的。

如果你加熱一種物質，它會開始發光，因為其中的原子會發出光（因此有“紅熱”這個詞）。鈉路燈發出的黃橙色光就是一個很好的例子：鈉原子主要在可見光譜的黃色部分，波長為590奈米處發光。當原子內的電子在能級之間“躍遷”時，原子會吸收或釋放光，光的精確頻率取決於能級之間的能量差。因此，加熱材料發出的光的頻率為我們提供了原子不同能級之間間隙的“地圖”。解釋這些原子發射是20世紀上半葉物理學家們努力解決的問題之一。這個問題直接導致了量子力學的發展，而希爾伯特的譜理論數學發揮了主要作用。

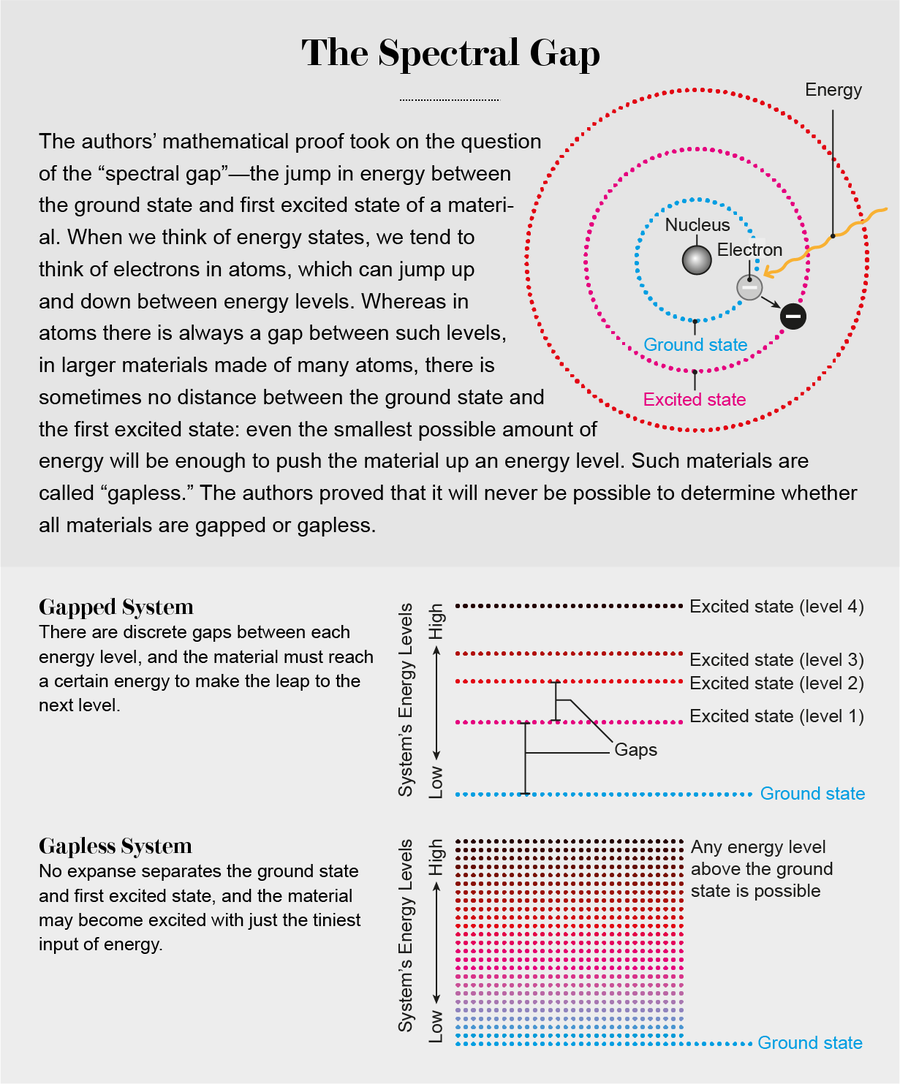
量子能級之間的這些間隙中，有一個特別重要。物質的最低可能能級稱為其基態。這是它在沒有熱量時的狀態。為了使物質進入基態，科學家必須在實驗室中將其冷卻到極低的溫度。然後，如果物質要做任何不同於處於基態的事情，就必須將其激發到更高的能量。最簡單的方法是吸收它可以吸收的最小能量，剛好足以將其帶到高於基態的下一個能級——第一激發態。基態和第一激發態之間的能量間隙非常關鍵，以至於它通常被稱為譜隙。

在某些材料中，基態和第一激發態之間存在很大的間隙。在另一些材料中，能級一直延伸到基態，沒有任何間隙。材料是“有隙”還是“無隙”對其在低溫下的行為具有深遠的影響。它在量子相變中起著尤為重要的作用。

當材料的性質發生突然而劇烈的變化時，就會發生相變。我們都非常熟悉一些相變——例如水從固態冰轉變為液態。但是，即使溫度保持在極低的水平，也會發生更奇特的量子相變。例如，改變材料周圍的磁場或對其施加的壓力會導致絕緣體變成超導體，或導致固體變成超流體。

材料如何在絕對零度（−273.15攝氏度）的溫度下發生相變？在絕對零度下，根本沒有熱量來提供能量。這歸結為譜隙。當譜隙消失——當材料無隙時——達到激發態所需的能量變為零。最微小的能量也足以推動材料發生相變。事實上，由於在這些極低溫度下主導物理學的奇怪量子效應，材料可以暫時從虛空中“借用”這種能量，經歷相變，然後“歸還”能量。因此，為了理解量子相變和量子相，我們需要確定材料何時有隙以及何時無隙。

由於譜隙問題對於理解物質的量子相如此根本，因此它在理論物理學的各個領域中都會出現。凝聚態物理學中許多著名且長期存在的開放性問題都歸結為解決特定材料的這個問題。一個密切相關的問題甚至出現在粒子物理學中：有非常好的證據表明，描述夸克及其相互作用的基本方程具有“質量間隙”。來自日內瓦附近大型強子對撞機等粒子對撞機的實驗資料以及來自超級計算機的大量數值計算結果都支援這一觀點。但是，從理論上嚴格證明這一觀點似乎極其困難。事實上，這個問題被稱為楊-米爾斯質量間隙問題，已被克萊數學研究所命名為七個千禧年難題之一，任何解決它的人都有權獲得100萬美元的獎金。所有這些問題都是一般譜隙問題的特例。但是，對於任何試圖解決這些問題的人來說，我們都有壞訊息。我們的證明表明，一般問題比我們想象的還要棘手。原因歸結為一個稱為判定問題的問題。

無法回答的問題

到20世紀20年代，希爾伯特開始關注將數學的基礎建立在堅實、嚴謹的基礎上——這一努力被稱為希爾伯特綱領。他認為，無論人們提出什麼數學猜想，原則上都有可能證明它是真的還是假的。（最好不要證明它既是真又是假，否則數學就出問題了！）這個想法似乎很明顯，但數學是關於絕對確定地建立概念的。希爾伯特想要一個嚴謹的證明。

1928年，他提出了判定問題。英文翻譯為“the decision problem”。它詢問是否存在一種程式或“演算法”，可以判定數學陳述是真還是假。

例如，陳述“任何整數乘以2都得到一個偶數”都可以很容易地使用基本邏輯和算術證明為真。其他陳述則不太清楚。以下面的例子為例：“如果你取任何整數，並重復將其乘以3，如果是奇數則加1，如果是偶數則除以2，你總是最終會得到數字1。”（請思考一下。）

不幸的是，希爾伯特的希望破滅了。1931年，哥德爾發表了一些非凡的成果，現在被稱為他的不完備性定理。哥德爾證明，關於整數的完全合理的數學陳述，既不能被證明也不能被證偽。從某種意義上說，這些陳述超出了邏輯和算術的範圍。並且他證明了這個斷言。如果這很難理解，你並不孤單。哥德爾的不完備性定理動搖了數學的根基。

以下是哥德爾思想的精髓：如果有人告訴你“這句話是謊言”，那麼這個人是在說真話還是在說謊？如果他或她在說真話，那麼這個陳述一定確實是謊言。但如果他或她在說謊，那麼它就是真的。這種困境被稱為說謊者悖論。即使它看起來是一個完全合理的英語句子，也沒有辦法確定它是真還是假。哥德爾設法做的是僅使用基本算術構建了說謊者悖論的嚴格數學版本。

判定問題故事中的下一個主要人物是英國計算機科學家艾倫·圖靈。圖靈因其在二戰期間破解德國恩尼格瑪密碼中的作用而在公眾中最為出名。但在科學家中，他最出名的是他1937年的論文《論可計算數及其在判定問題中的應用》。年輕的圖靈深受哥德爾結果的影響，他對希爾伯特的判定問題給出了否定回答，證明不存在可以判定數學陳述是真還是假的一般演算法。（美國數學家阿隆佐·邱奇也在圖靈之前獨立地證明了這一點。但圖靈的證明最終更重要。通常在數學中，一個結果的證明比結果本身更重要。）

為了解決判定問題，圖靈必須精確地定義“計算”某物的含義。如今，我們認為計算機是放在我們桌子上、膝蓋上甚至口袋裡的電子裝置。但我們所知的計算機在1936年並不存在。事實上，“計算機”最初指的是用筆和紙進行計算的人。然而，像你在高中時那樣用筆和紙進行計算，在數學上與使用現代臺式計算機進行計算沒有什麼不同——只是慢得多，而且更容易出錯。

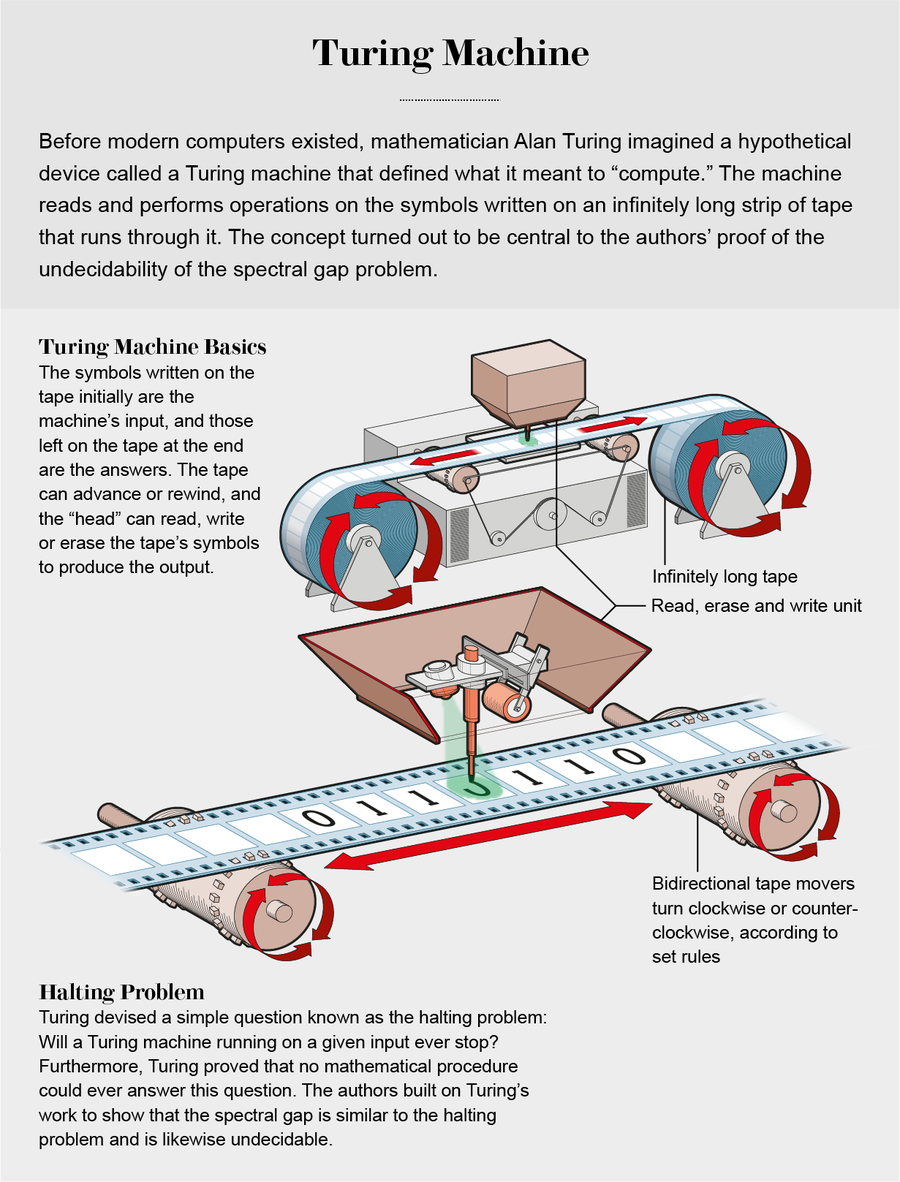
圖靈提出了一個理想化的、虛構的計算機，稱為圖靈機。這種非常簡單的虛構機器看起來不像現代計算機，但它可以計算最強大的現代計算機可以計算的一切。事實上，任何可以計算的問題（即使是在量子計算機或31世紀尚未發明的計算機上）也可以在圖靈機上計算。只是圖靈機需要更長的時間。

圖靈機有一條無限長的帶子和一個“頭”，它可以一次在帶子上讀取和寫入一個符號，然後沿帶子向右或向左移動一步。計算的輸入是最初寫在帶子上的任何符號，輸出是當圖靈機最終停止執行（停止）時留在帶子上的任何內容。圖靈機的發明甚至比判定問題的解決方案更重要。透過對計算的含義給出精確的、數學上嚴謹的表述，圖靈創立了現代計算機科學領域。

在構建了他的計算機的虛構數學模型之後，圖靈繼續證明，關於圖靈機有一個簡單的問題，任何數學程式都無法判定：在給定輸入的情況下執行的圖靈機是否會停止？這個問題被稱為停機問題。當時，這個結果令人震驚。數學家們已經習慣了這樣一個事實，即我們正在研究的任何猜想都可能是可證明的、可證偽的或不可判定的。

我們的貢獻

在我們的結果中，我們不得不將所有這些分散的線索重新聯絡起來。我們想將譜隙的量子力學、不可判定性的計算機科學和希爾伯特的譜理論結合起來，以證明——就像停機問題一樣——譜隙問題是哥德爾和圖靈教給我們的那些不可判定問題之一。

2012年，在塞費爾德那家咖啡館裡聊天時，我們想到了如何證明一個與譜隙相關的較弱的數學結果。我們討論了這個想法，甚至沒有在餐巾紙背面亂塗亂畫，而且它似乎是可行的。然後下一場會談開始了。我們就此擱置了它。

幾個月後，我們中的一人（託比·庫位元）拜訪了慕尼黑的邁克爾，我們做了我們在塞費爾德沒有做的事情：在紙片上潦草地寫下了一些方程式，並確信這個想法是可行的。在接下來的幾周裡，我們完成了論證，並在一個四頁的私人筆記中正確地寫了下來。（在數學中，在你寫下來——或者更好的是，打出來並展示給同事審查之前，沒有任何東西是真正被證明的。）從概念上講，這是一個重大進步。在那之前，證明譜隙不可判定性的想法與其說是嚴肅的前景，不如說是一個玩笑。現在我們第一次看到了它實際上可能實現的曙光。但這仍然有很長的路要走。我們無法擴充套件我們最初的想法來證明譜隙問題本身是不可判定的。

熬夜苦幹

我們試圖透過將譜隙問題與量子計算聯絡起來來實現下一步飛躍。1985年，諾貝爾獎獲得者物理學家理查德·費曼發表了一篇論文，啟動了量子計算機的想法。在那篇論文中，費曼展示瞭如何將量子系統的基態與計算聯絡起來。計算是一個動態過程：你向計算機提供輸入，它經過幾個步驟來計算結果並輸出答案。但是量子系統的基態是完全靜態的：基態只是材料在零溫度下所處的配置，什麼也不做。那麼它如何進行計算呢？

答案來自於量子力學的定義特徵之一：疊加，即物體同時佔據多種狀態的能力，例如，埃爾溫·薛定諤著名的量子貓可以同時處於活和死的狀態。費曼提出構建一種量子態，該量子態處於計算各個步驟的疊加態——初始輸入、計算的每個中間步驟和最終輸出——全部同時進行。加州理工學院的阿列克謝·基塔耶夫後來透過構建一種虛構的量子材料，其基態看起來完全像這樣，從而大大發展了這個想法。

如果我們使用基塔耶夫的構造將圖靈機的整個歷史以疊加態放入材料的基態中，我們能否將停機問題轉化為譜隙問題？換句話說，我們能否證明，任何解決譜隙問題的方法也會解決停機問題？由於圖靈已經證明停機問題是不可判定的，這將證明譜隙問題也一定是不可判定的。

將停機問題編碼到量子態中並不是一個新想法。現在在麻省理工學院的塞思·勞埃德早在近二十年前就提出了這個想法，以證明另一個量子問題的不可判定性。滑鐵盧 Perimeter 理論物理研究所的丹尼爾·戈特斯曼和加州大學歐文分校的桑迪·伊拉尼使用基塔耶夫的想法證明，即使是相互作用的量子粒子的單行線也可能表現出非常複雜的行為。事實上，我們希望利用的是戈特斯曼和伊拉尼版本的基塔耶夫構造。

但是譜隙是一個不同型別的問題，我們面臨著一些顯然難以逾越的數學障礙。第一個障礙與向圖靈機提供輸入有關。請記住，停機問題的不可判定性是關於圖靈機在給定輸入的情況下是否會停止。我們如何設計我們的虛構量子材料，使其能夠讓我們選擇要編碼在基態中的圖靈機輸入？

在研究早期的問題（我們仍然在塞費爾德的咖啡館裡陷入困境的那個問題）時，我們想到了如何透過在粒子之間的相互作用中加入“扭曲”並使用這種旋轉角度來建立圖靈機的輸入，從而糾正這個問題。2013年1月，我們在北京的一次會議上會面，共同討論了這個計劃。但我們很快意識到，我們必須證明的東西非常接近於與關於量子圖靈機的已知結果相矛盾。我們決定，在進一步推進該專案之前，我們需要一個完整而嚴謹的證明，證明我們的想法是可行的。

此時，託比已經在馬德里康普頓斯大學大衛·佩雷斯-加西亞的研究小組工作了兩年多。同月，他搬到了劍橋大學，但他在那裡的新公寓尚未準備好，因此他的朋友和量子資訊理論家同事阿什利·蒙塔納羅提出要收留他。在那兩個月裡，他開始著手對這個想法進行嚴格的證明。他的朋友早上會在廚房的桌子上發現他，旁邊放著一排空咖啡杯，準備睡覺，他通宵工作，弄清楚細節並將它們打出來。在那兩個月結束時，託比發出了完成的證明。

為了紀念過去的鋪磚

這份29頁的證明展示瞭如何克服將量子材料的基態與圖靈機計算聯絡起來的障礙之一。但是，實現該目標甚至存在更大的障礙：由此產生的量子材料始終是無隙的。如果它始終是無隙的，那麼對於這種特定材料的譜隙問題就非常容易解決：答案是無隙！

我們最初在塞費爾德提出的想法，雖然證明的結果比我們想要的要弱得多，但仍然設法繞過了這個障礙。關鍵是使用“鋪磚”。想象一下你要用瓷磚覆蓋一個大的浴室地板。事實上，想象一下這是一個無限大的浴室。瓷磚上的圖案非常簡單：瓷磚的四個邊每個邊都是不同的顏色。你有很多箱瓷磚，每箱瓷磚的顏色排列都不同。現在想象一下，每箱瓷磚都有無限供應。你當然希望鋪滿無限大的浴室地板，使相鄰瓷磚上的顏色匹配。這有可能嗎？

答案取決於你有哪些箱瓷磚可用。使用某些彩色瓷磚組，你將能夠鋪滿無限大的浴室地板。使用另一些，你將無法做到。在你選擇購買哪些箱瓷磚之前，你想知道它們是否有效。對你來說不幸的是，1966年，數學家羅伯特·伯格證明了這個問題是不可判定的。

鋪滿無限大的浴室地板的一種簡單方法是首先鋪一個小矩形，使其相對兩側的顏色匹配。然後你可以透過重複這個矩形圖案來覆蓋整個地板。由於這些圖案每隔幾個瓷磚重複一次，因此被稱為週期性的。鋪磚問題不可判定的原因是也存在非週期性鋪磚：覆蓋無限大地板但永不重複的圖案。

當我們討論我們最初的小結果時，我們研究了加州大學伯克利分校的拉斐爾·M·羅賓遜在1971年對伯格原始證明進行的簡化。羅賓遜構建了一組56種不同的瓷磚，當用於鋪設地板時，會產生越來越大的正方形的互鎖圖案。這種分形圖案看起來是週期性的，但事實上，它永遠不會完全重複自身。我們廣泛討論了使用鋪磚結果來證明量子性質不可判定性的方法。但當時，我們甚至沒有考慮譜隙。這個想法一直處於休眠狀態。

2013年4月，託比拜訪了IBM托馬斯·J·沃森研究中心的查理·貝內特。在成為量子資訊理論的奠基人之一之前，貝內特的眾多成就之一是他在20世紀70年代在圖靈機方面做出的開創性工作。我們想就我們證明中的一些技術細節向他請教，以確保我們沒有忽略某些東西。他說他已經40年沒有考慮過這些東西了，現在是年輕一代接手的時候了。（然後他非常樂於助人地解釋了他20世紀70年代工作的一些微妙的數學細節，這使我們確信我們的證明是沒問題的。）

貝內特擁有大量的科學知識。由於我們一直在談論圖靈機和不可判定性，他透過電子郵件傳送了幾篇他認為我們可能會感興趣的關於不可判定性的舊論文的副本。其中一篇就是羅賓遜在1971年發表的同一篇論文，我們之前研究過。現在，在我們早期的討論中播下的種子到了煥發生機的時候了。再次閱讀羅賓遜的論文，我們意識到這正是我們防止譜隙消失所需要的。

我們最初的想法是將圖靈機的一個副本編碼到基態中。透過仔細設計粒子之間的相互作用，如果圖靈機停止，我們可以使基態能量稍微升高。然後，譜隙——到第一激發態的能量躍遷——將取決於圖靈機是否停止。這個想法只有一個問題，而且是一個大問題。隨著粒子數量的增加，對基態能量的額外貢獻越來越接近於零，導致材料始終是無隙的。

但是透過改編伯格的鋪磚構造，我們可以將許多副本完全相同的圖靈機編碼到基態中。事實上，我們可以將一個副本附加到羅賓遜鋪磚圖案中的每個正方形。由於這些是同一圖靈機的相同副本，如果其中一個停止，則它們全部停止。來自所有這些副本的能量貢獻會累加起來。隨著粒子數量的增加，鋪磚圖案中的正方形數量變得更大。因此，圖靈機的副本數量增加，它們的能量貢獻變得巨大，這為我們提供了譜隙的可能性。

考試和截止日期

我們證明的結果仍然存在一個重大的弱點。我們無法說明當材料有隙時，能量間隙有多大。這種不確定性使我們的結果容易受到批評，即間隙可能非常小，以至於它可能根本不存在。我們需要證明，當間隙存在時，實際上是很大的。當我們考慮三維材料而不是我們之前一直在考慮的平面材料時，我們找到了第一個解決方案。

當你無法停止思考一個數學問題時，你會在最意想不到的地方取得進展。大衛在監考時，在腦海中研究了這個想法的細節。在考場裡沿著一排排桌子走動時，他對周圍學生們緊張地考試渾然不覺。一旦考試結束，他就將證明的這部分寫在紙上。

我們現在知道獲得大的譜隙是可能的。我們也可以在二維中獲得它嗎，還是必須是三維的？記住鋪滿無限大的浴室地板的問題。我們需要證明的是，對於羅賓遜鋪磚，如果你在某個地方放錯了一塊瓷磚，但其他地方的顏色仍然匹配，那麼瓷磚形成的圖案只會以這塊錯放的瓷磚為中心在一個小區域內被破壞。如果我們能證明羅賓遜鋪磚的這種“魯棒性”，那就意味著沒有辦法透過僅稍微破壞鋪磚來獲得小的譜隙。

到2013年夏末，我們覺得我們已經掌握了證明工作所需的所有要素。但仍有一些重要的細節需要解決，例如證明鋪磚的魯棒性可以與所有其他證明要素合併，從而給出完整的結果。劍橋大學的艾薩克·牛頓數學科學研究所將在2013年秋季學期舉辦一個關於量子資訊的特別研討會。我們三人都被邀請參加。這是共同完成該專案的絕佳機會。但大衛無法在劍橋待太久。我們決心在他離開之前完成證明。

艾薩克·牛頓研究所到處都有黑板——甚至在浴室裡！我們選擇了走廊裡的一個黑板（離咖啡機最近的那個）進行討論。我們花了很長時間在黑板上推導缺失的想法，然後將使這些想法在數學上嚴謹的任務分配給我們。這個過程總是比在黑板上看起來花費更多的時間和精力。隨著大衛離開日期的臨近，我們整天和大部分晚上都不間斷地工作。就在他回家前幾個小時，我們終於得到了一個完整的證明。

在物理學和數學領域，研究人員通常透過在arXiv.org預印本伺服器上釋出論文草稿，然後在提交給期刊進行同行評審之前，首次公開大部分研究成果。儘管我們現在相當確信整個論證是可行的，最困難的部分已經過去，但我們的證明尚未準備好釋出。還有許多數學細節需要補充。我們還想重寫和整理論文（我們希望在此過程中減少頁數，儘管在這方面我們將徹底失敗）。最重要的是，儘管我們中至少有一個人檢查了證明的每個部分，但沒有人從頭到尾完整地看過一遍。

2014年夏天，大衛在慕尼黑工業大學與邁克爾一起休假。託比出去加入了他們。計劃是花時間逐行檢查和完成整個證明。大衛和託比共用一間辦公室。每天早上，大衛都會帶著一份新的論文草稿列印稿、大量的筆記以及潦草地寫在頁邊和夾頁上的問題來到辦公室。我們三個人會喝咖啡，然後從我們昨天停下的地方繼續，在黑板上討論證明的下一部分。下午，我們分工合作，重寫論文，新增新材料，並瀏覽證明的下一部分。託比患有椎間盤突出，無法坐下，因此他將筆記型電腦放在桌子上倒扣的垃圾桶上工作。大衛坐在對面，越來越多的列印稿和筆記佔據了他越來越多的辦公桌。在幾次情況下，我們發現了證明中的重大漏洞。這些漏洞最終被證明是可以克服的，但彌合這些漏洞意味著要新增大量材料。頁數繼續增加。

在六週後，我們檢查、完成並改進了證明的每一行。還需要六個月才能完成所有的撰寫工作。最終，在 2015 年 2 月，我們將論文上傳到了 arXiv.org。

這一切意味著什麼

這 146 頁複雜的數學最終告訴了我們什麼？

首先，也是最重要的，它們給出了一個嚴格的數學證明，證明量子物理學的基本問題之一通常是無法解決的。請注意，這裡的“通常”至關重要。即使停機問題通常是不可判定的，但對於圖靈機的特定輸入，通常仍然有可能判斷它是否會停機。例如，如果輸入的第一個指令是“停機”，答案就很清楚。如果第一個指令告訴圖靈機永遠迴圈，情況也是如此。因此，儘管不可判定性意味著譜隙問題對於所有材料都無法解決，但對於特定材料來說，完全有可能解決它。事實上，凝聚態物理學中充滿了這樣的例子。儘管如此，我們的結果嚴格證明，即使對材料粒子之間的微觀相互作用進行完美、完整的描述，也並不總是足以推匯出其宏觀性質。

您可能在問自己，這一發現對“真實的物理學”有何影響。畢竟，科學家總是可以嘗試在實驗中測量譜隙。想象一下，如果我們能夠從我們的數學證明中設計出量子材料，並在實驗室中製造出一塊。它的相互作用非常複雜，遠遠超出了科學家們可能做到的任何事情。但是，如果我們能夠做到這一點，然後取一塊材料並嘗試測量其譜隙，該材料不能簡單地攤手說：“我無法告訴你——它是不可判定的。”實驗必須測量某些東西。

這個明顯的悖論的答案在於，嚴格來說，“有隙”和“無隙”這兩個術語只有在材料無限大的時候才有數學意義。現在，即使是非常小的一塊材料中包含的約 10²³ 個原子也代表著一個非常大的數字。對於普通材料來說，這已經非常接近無窮大了，以至於可以忽略不計。但是，對於我們的證明中構建的非常奇怪的材料來說，大並不等同於無窮大。也許對於 10²³ 個原子，材料在實驗中看起來是無隙的。為了確保這一點，您取一個尺寸是原來兩倍的材料樣本並再次測量。仍然是無隙的。然後，在深夜，您的研究生走進實驗室，只添加了一個額外的原子。第二天早上，當您再次測量時，材料變成了有隙的！我們的結果證明，這種轉變可能發生的大小是不可計算的（與您現在熟悉的哥德爾-圖靈意義相同）。這個故事目前完全是假設性的，因為我們無法設計出如此複雜的材料。但這透過嚴格的數學證明表明，科學家在推斷更大尺寸下相同材料的行為時，必須格外小心地推斷實驗結果。

在本文描述的工作完成後，我們繼續將其擴充套件到一維繫統和相圖。此後，量子物理學中的其他重要問題也被證明可以使用計算機科學的技術來判定為不可判定，這對數學產生了深遠的影響。1935 年，愛因斯坦、波多爾斯基和羅森意識到，量子力學預測了他們所謂的“幽靈般的超距作用”——糾纏量子粒子對之間的關聯，這在經典物理學中是不可能的。在一次重大突破中，由悉尼科技大學的季錚鋒領導的團隊最近宣佈了一項結果，證明即使在一定的合理精度範圍內，估計這種關聯在一般情況下也是不可判定的。他們的結果反駁了數學中一個懸而未決 40 多年的深刻猜想。

現在我們回到楊-米爾斯問題——描述夸克及其相互作用的方程是否具有質量間隙的問題。計算機模擬表明答案是肯定的，但我們的結果表明，確定答案可能又是另一回事。如果我們將模擬稍微擴大一點，楊-米爾斯質量間隙的計算機模擬證據是否會消失？我們的結果無法說明，但它確實為楊-米爾斯問題以及其他對物理學家重要的問題可能是不可判定的這一有趣的可能打開了大門。

那麼，我們多年前在奧地利阿爾卑斯山的一家咖啡館裡試圖證明的最初的、微小的且不太重要的結果呢？實際上，我們仍在研究它。