三體問題

到 2014 年春天，我基本上已經放棄了三體問題。由於沒有想法，我開始在我的筆記型電腦上程式設計，以生成和搜尋近似解。

這些嘗試永遠無法徹底解決我的問題，但它們可能會為答案收集證據。我缺乏程式設計專業知識以及由此產生的不耐煩減慢了程序，這對像我這樣喜歡紙筆的數學家來說是一種不愉快的體驗。我找到了我的老朋友卡爾斯·西蒙，巴塞羅那大學的一位教授，說服他幫助我進行笨拙的搜尋。

那年秋天，我前往西班牙與西蒙會面，他以其在天體力學領域最有創意和最細緻的數值分析師之一而聞名。他也是一個直率的人，不會浪費時間或拐彎抹角。我在他辦公室的第一個下午，在我解釋了我的問題之後，他用銳利的目光看著我，問道：“理查德，你為什麼關心？”

關於支援科學新聞報道

如果您喜歡這篇文章，請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱，您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。

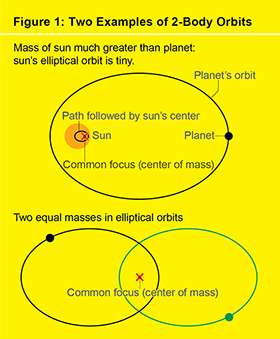
答案可以追溯到三體問題的起源。艾薩克·牛頓最初提出並解決了二體問題（見圖 1），當時他在 1687 年出版了他的《原理》。他問道：“如果作用在兩個質量上的唯一力是它們彼此的引力，那麼這兩個質量在空間中將如何運動？” 牛頓將這個問題構建為求解微分方程組的問題——這些方程根據物體當前的位置和速度來決定物體未來的運動。他完全解決了他的二體方程。這些解，也稱為軌道，使每個物體都沿著圓錐曲線——圓、橢圓、拋物線或雙曲線運動。在找到所有可能的軌道時，牛頓推匯出了約翰內斯·開普勒的行星運動定律，開普勒在 1609 年釋出的經驗定律，綜合了他已故僱主第谷·布拉赫數十年的天文觀測。開普勒第一定律指出，每顆行星（或彗星）都沿著以太陽為焦點的圓錐曲線運動。然而，在牛頓的解中，這兩個物體——太陽和行星——在兩個獨立的圓錐曲線上運動。這些圓錐曲線共享一個焦點，即兩個物體的質心。太陽比任何行星都重得多，以至於太陽-行星系統的質心位於太陽內部，非常靠近太陽的質心，太陽的質心幾乎不會在共同中心周圍以微小的橢圓路徑擺動。

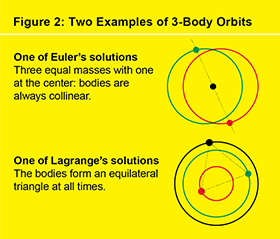
用三個質量代替兩個質量，你就得到了三體問題。與其前身一樣，它的軌道是微分方程組的解。然而，與其前身不同的是，找到軌道的顯式公式幾乎是不可能的。時至今日，儘管有現代計算機和一些最優秀的物理學家和數學家進行了數百年的工作，我們仍然只有五個軌道族的顯式公式，其中三個是由萊昂哈德·尤拉（1767 年）發現的，兩個是由約瑟夫-路易斯·拉格朗日（1772 年）發現的（見圖 2）。1890 年，亨利·龐加萊在三體問題中發現了混沌動力學，這一發現意味著我們永遠無法像牛頓對二體問題的完整解那樣，在細節層面上了解該問題的所有解。然而，透過一種稱為數值積分的過程，在計算機上高效完成，我們仍然可以生成近似軌道的有限段，這個過程對於空間任務的規劃至關重要。透過延長計算機的執行時間，我們可以使近似值達到我們想要的精度。

日食

西蒙的話讓我喘不過氣來。“當然，我在乎，”我想。“我研究這個問題已經快二十年了！” 事實上，我一直專注於問題中的一個特定問題，這個問題讓我很感興趣

每個週期性日食序列是否都是平面三體問題的某個週期性解的日食序列？

讓我解釋一下。想象一下三個物體——把它們想象成恆星或行星——在一個平面上運動，彼此之間施加引力。將物體編號為一、二和三。有時，所有三個物體將對齊成一條直線（見圖 3）。將這些時刻視為日食。（從技術上講，這種“日食”稱為合朔，是一個在絞刑遊戲中無與倫比的詞。）隨著時間的推移，記錄每次發生的日食，並將其標記為一、二或三，以表示哪顆恆星在中間。透過這種方式，我們得到一個由一、二和三組成的列表，稱為日食序列。

例如，在我們簡化的太陽-地球-月球系統中，月球（我們將其標記為物體“3”）每月繞地球（物體“2”）轉一圈，而地球每年繞太陽（物體“1”）轉一圈。這種運動是重複的，所以它會給我們一個週期性的日食序列。具體來說：2、3、2、3、2、3、2、3、2、3、2、3、2、3、2、3、2、3、2、3、2、3、2、3。序列中沒有 1，因為太陽永遠不會落在地球和月球之間。一年中，該列表長 24 個數字，一年 12 個月，每個月都有一個 2、3。

解決方案的日食序列沒有理由必須重複自身。它可能會永遠持續下去，沒有明顯的模式。但是，如果解決方案在一段時間後完全重複自身，就像地球-月球-太陽系統在一年後一樣，那麼序列會重複：地球-月球-太陽系統的相同 24 個數字每年都會重播。所以，回到我的問題：每個週期性日食序列是否都是平面三體問題的某個週期性解的日食序列？我懷疑答案是肯定的，但我無法證明。

帶孔物體

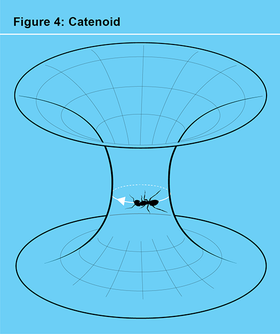
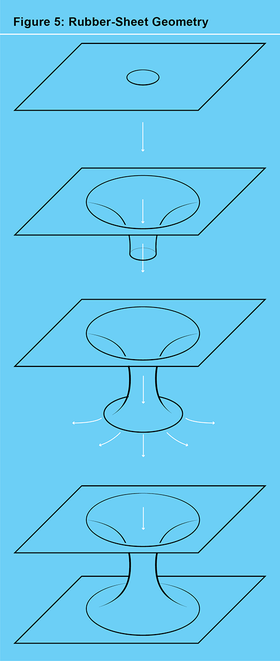
為了證明我的問題的重要性，我提醒西蒙一個基本事實，它將數學的三個分支聯絡在一起：拓撲學，有時稱為橡皮膜幾何；黎曼幾何，彎曲曲面的研究；以及動力學，事物運動方式的研究。想象一隻蟲子沿著一個彎曲的表面行走，這個表面形狀像“蟲洞表面”，也稱為懸鏈面（見圖 4）。蟲子的工作是找到繞孔一週的最短迴路。就拓撲學而言，蟲洞表面（見圖 5）與x-y平面上穿了一個孔的表面相同。實際上，想象一下一個孔穿過一塊柔性橡皮膜。透過向下推孔並向外拉伸它，你可以製作出蟲洞表面。如果孔已經充分向外張開，那麼不僅存在這個最短迴路，而且它還滿足一個非常類似於三體方程的微分方程。透過這種方式，我們的蟲子找到了一個有趣的微分方程的週期解。

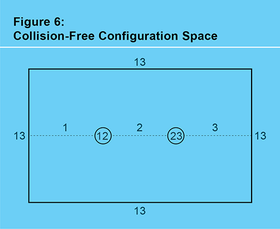
在三體問題中，蟲洞表面的作用由稱為配置空間的東西來扮演——一個空間，其點同時編碼所有三個物體的位置，因此配置空間中的一條曲線指定了三個物體中每個物體的運動。透過堅持我們的物體不相互碰撞，我們在配置空間中穿孔。正如我們將看到的，就拓撲學或橡皮膜幾何而言，由此產生的無碰撞配置空間與x-y平面上穿了兩個孔的平面相同（見圖 6）。我們將孔標記為“12”，表示物體 1 和 2 發生了碰撞，將孔標記為“23”，表示物體 2 和 3 發生了碰撞，並將孔放在x軸上。我們還將在無窮遠處放置第三個孔，並將其標記為“13”，以表示物體 1 和 3 碰撞。這些孔將x軸分成三個段，分別標記為 1、2 和 3。這個兩次穿孔平面中的一條曲線表示所有三個物體的運動——也就是說，三體問題的潛在解。當曲線穿過段 1 時，表示發生了 1 型日食，同樣，穿過段 2 或 3 時也是如此。透過這種方式，日食序列表示圍繞我們的碰撞孔纏繞的方式。

現在，我們的蟲子試圖最小化其路徑的長度，因為它繞著蟲洞繞了一圈。為了獲得蟲子問題和三體問題之間的正確類比，我們必須用一個稱為路徑作用量的量代替路徑的長度。（作用量是路徑表示的運動的瞬時動能減去勢能的平均值。）力學中一個古老的定理指出，配置空間中任何最小化作用量的曲線都必須是牛頓三體問題的解。因此，我們可以嘗試透過在產生固定日食序列的所有閉合路徑中搜索那些最小化作用量的閉合路徑來解決我們的日食序列問題。

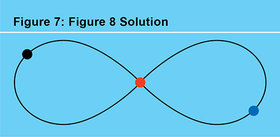
這種策略——在配置空間中為具有特定日食序列的環路尋求最小化作用量——在過去 17 年的大部分時間裡一直困擾著我，並導致了許多不錯的結果。例如，在 2000 年，巴黎狄德羅大學的阿蘭·切辛納和我重新發現了似乎是零角動量三體問題的第一個已知週期解。這是一個 8 字形解（見圖 7），最早由聖塔菲研究所的克里斯·摩爾在 1993 年發現。在這種情況下，三個質量相等的物體在平面上沿著 8 字形相互追逐。它的日食序列是 123123，永遠重複。我們的工作普及了 8 字形，並給出了嚴格的存在性證明。它還導致了對等質量N體問題的許多新軌道的爆炸式發現，這些軌道被西蒙（見圖 8）命名為“舞蹈”，他發現了數百個這些新的軌道族。我們的 8 字形軌道甚至進入了劉慈欣的暢銷中國科幻小說，其英文譯名為《三體問題》。

在我與西蒙分享我的思考的第二天早上，他說了一些深深影響我的話。“理查德，如果你對你的問題的想法是真的，那麼一定存在一種動力學機制。” 換句話說，如果我對我問題的答案是肯定的看法是正確的，那麼一定存在一些關於這些物體如何運動的因素使之如此。

這幾個字讓我質疑我的信念，並讓我放棄了長達 17 年的嘗試，即透過最小化路徑的作用量來回答我的問題。我對這個問題中的哪些動力學機制有所瞭解？我想知道。我能想到兩種，其中只有一種抱有希望。這種機制與龐加萊發現的混沌有關，它讓我反思了我最近的一位合作者，明尼蘇達大學的裡克·莫克爾的舊作。在 20 世紀 80 年代，他展示了來自三體問題中的三重碰撞的稱為雙曲纏結的曲線如何導致驚人的結果。當我重讀他的舊論文時，我覺得莫克爾掌握了我問題的關鍵。我聯絡了他，幾天之內，莫克爾和我回答了我的問題！好吧，幾乎。我們回答了一個無限接近的問題。

形狀球體

理解莫克爾的動力學機制，以及三體配置空間與上面描述的帶有兩個孔的平面之間的關係，需要思考一個稱為形狀球體的物體。當三個物體在平面上移動時，它們在每個瞬間都形成三角形的三個頂點。與其跟蹤每個頂點的位置，不如只跟蹤三角形的整體形狀。結果是形狀球體上的曲線，形狀球體是一個球體，其點表示三角形的“形狀”。

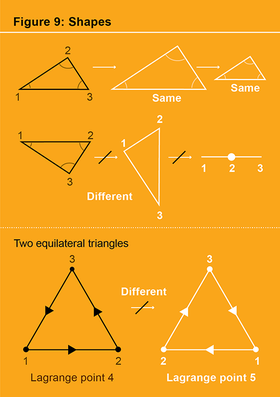
什麼是“形狀”？如果我們可以透過平移、旋轉或縮放一個圖形將其變成另一個圖形，則平面中的兩個圖形具有相同的形狀（見圖 9）。從通常的三體配置空間（也就是說，從瞭解三角形所有三個頂點的位置）傳遞到形狀球體中的點的操作是一個遺忘的過程——忘記三角形的大小、其質心的位置以及三角形在平面中的方向。形狀球體是二維的，這很容易從高中幾何學中理解：如果我們知道三角形的所有三個角，我們就知道三角形的形狀，但由於三個角的總和始終為 180 度，我們實際上只需要三個角中的兩個角——因此，兩個數字足以描述三角形的形狀。形狀球體實際上是一個球體，這更難理解，並且要求我們允許三角形退化，也就是說，我們允許由位於同一條線上的三個頂點組成的“三角形”被稱為三角形。這些所謂的退化零面積三角形構成了形狀球體的赤道：它們就是日食！

三角形的面積除以其大小 (r) 的平方，是其到赤道的距離。球體的北極和南極代表那些具有最大可能面積的三角形，並且是兩個等邊三角形形狀。但是為什麼有兩個等邊形狀呢？這兩個等邊三角形形狀因其頂點的迴圈順序而不同（見圖 9）。無法透過平面的旋轉、平移或縮放將其中一個等邊三角形變成另一個等邊三角形：它們代表不同的形狀。然而，在平面中繞一條線（任何線）反射的操作會將一個等邊三角形形狀變成另一個等邊三角形形狀。這種反射操作作用於所有三角形，因此也作用於形狀球體本身，在形狀球體中，它透過繞赤道反射來起作用，保持赤道（退化三角形）的點固定，同時交換南北半球。

在退化三角形中，包括二元碰撞：那些“三角形”，其中三個頂點中的兩個頂點彼此重疊。恰好有三個這樣的二元碰撞三角形，標記為“12”、“23”和“13”，具體取決於哪兩個頂點彼此重疊。

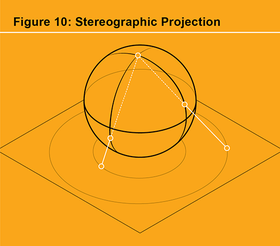
我現在可以解釋形狀球體如何向我們展示三體配置空間在拓撲上與通常的x-y平面減去兩個點相同。我們必須知道，球體減去一個點在拓撲上與通常的x-y平面是相同的物件（見圖 10）。瞭解關於球體的這個事實的一種方法是使用球面投影，它將移除了單個點（“光源”）的球體對映到通常的x-y平面上。當球體上的一個點趨向於光源時，它在x-y平面上的影像點會移動到無窮遠，因此我們也可以說，添加了無窮遠點的平面在拓撲上等於球體。將光源視為形狀球體的 13 二元碰撞點，以便x-y平面的無窮遠點對應於 13 碰撞點。定向球體，使其赤道面與x-y平面的x軸相交。然後球面投影將退化三角形的赤道對映到平面的x軸，而其他兩個二元碰撞點被對映到該x軸上的兩個點。透過這種方式，我們恰好得到了前面描述的圖片。

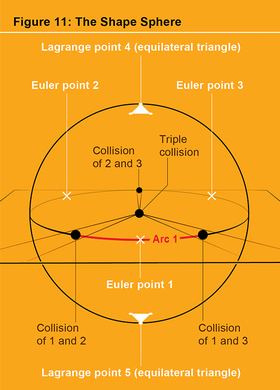
三個二元碰撞點在形狀球體上形成三個特殊點。除了這三個點之外，形狀球體上還有其他特殊點，稱為中心構型。這五個中心構型對應於尤拉和拉格朗日發現的五個解族。它們的解是唯一的三體解，其中三角形的形狀在三角形演化過程中不會改變！在拉格朗日解中，三角形在每個瞬間都保持等邊形；正如我們所見，存在兩種拉格朗日構型，它們構成了形狀球體的北極和南極（見圖 11）。我們將它們標記為“拉格朗日點 4”和“拉格朗日點 5”。其餘三個中心構型是尤拉構型，標記為“尤拉點 1”、“尤拉點 2”和“尤拉點 3”。它們是共線的（都在一條線上），退化的構型，因此它們位於
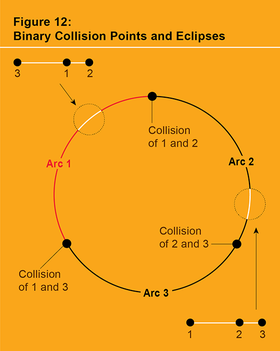
形狀球體的赤道。它們位於赤道上，介於三個二元碰撞點之間（見圖 12）。（它們沿赤道的間距取決於物體三個質量之間的質量比。）例如，尤拉點 1 位於標記為 1 的赤道弧上，因此是物體 1 位於物體 2 和 3 之間的共線形狀。（通常，所有五個中心構型點都稱為拉格朗日點，其中尤拉點標記為“L1”、“L2”和“L3”。）

人們可以透過掉落三個物體來理解中心構型解，我的意思是，讓三個物體從靜止開始，沒有初始速度。通常，當人們這樣做時，會發生各種瘋狂的事情：近距離二元碰撞、狂野的舞蹈，甚至可能是一個物體逃逸到無窮遠。但是，如果在一個物體以五個中心構型形狀之一排列時掉落這三個物體，那麼它們形成的三角形只會縮小到一個點，保持與開始時完全相同的形狀，三個質量均勻地相互拉動，直到解以同時三重碰撞結束。

通往三重碰撞的五條道路

三重碰撞是三體問題中的一個本質奇點，有點像問題中心的大爆炸，它是其大部分混沌和困難的根源。在 20 世紀初，芬蘭數學家卡爾·桑德曼證明，五個中心構型（如剛剛描述的掉落解所代表的那樣）是通往三重碰撞的唯一道路。這意味著任何以三重碰撞結束的解都必須以非常接近這五個掉落的中心構型解之一的方式接近它，並且隨著它越來越接近三重碰撞，解的形狀必須接近五個中心構型形狀之一。

桑德曼的工作是一項複雜的代數和分析壯舉。然後，在我高中畢業的那一年（完全沒有注意到三體問題），美國數學家理查德·麥戈希發明了他的所謂膨脹方法，該方法使我們能夠以圖形方式理解桑德曼的工作，並更詳細地研究三重碰撞附近的動力學。設 r 表示到三重碰撞的距離——三角形整體大小的度量。隨著 r 接近於零，牛頓方程變得非常糟糕，許多項趨於無窮大。麥戈希找到了配置空間變數和時間的變化，這減慢了接近三重碰撞的速度，並將三重碰撞點（即 r = 0）變成了一整組點：碰撞流形。驚喜！碰撞流形本質上是形狀球體。麥戈希的方法擴充套件了牛頓方程，最初牛頓方程僅對大於零的 r 有效，擴充套件為一個微分方程組，當 r = 0 時也有意義。

牛頓方程沒有平衡點，這意味著沒有三個物體的構型可以靜止不動：三顆恆星，彼此吸引，不能只是靜止在空間中而不移動。但是，當牛頓方程擴充套件到碰撞流形時，平衡點就出現了。恰好有 10 個平衡點，每個平衡點對形狀球體上的五個中心構型點中的每個點都有一對。一對中的一個元素表示相應掉落的中心構型在其接近三重碰撞時的最終結果。牛頓方程即使我們倒退時間也保持不變，因此我們可以反向執行任何解並獲得另一個解。當我們反向執行掉落的中心構型解時，我們會得到一個從三重碰撞中爆炸出來的解，在掉落的構型處達到其最大尺寸。該對的另一個元素表示此“爆炸”解的初始起點。這兩個中心構型解——碰撞和噴射——平滑地擬合在一起，形成一個單一的噴射-碰撞解，該解離開 r = 0 處的噴射平衡點，進入 r 大於零的區域，在該區域中，它達到最大尺寸，然後縮小以在三重碰撞流形上結束於那裡的碰撞平衡點。這個完整的解將平衡對的一個元素連線到另一個元素。

透過建立與中心構型相關的這些平衡點，這些平衡點深深地埋藏在三體問題中，麥戈希給了莫克爾一個金鑰，使他能夠應用現代動力學系統中的最新成果——牛頓、拉格朗日或桑德曼無法獲得的成果——從而在三體問題上取得一些有趣的進展。

莫克爾的遊走

在莫克爾的論文中，我看到了一張圖，其中有五個頂點，標記為中心構型，並透過邊連線在一起（見圖 13）。

圖上的遊走是穿過其頂點的可能迴路，沿著邊從一個頂點行進到另一個頂點。莫克爾證明，你可以在他的圖上進行的任何可能的遊走都對應於三體問題的解，該解在一段時間內接近於由相應頂點標記的中心構型解。例如，遊走 E1 L4 E2 L5 對應於一個非常接近與尤拉點 1 相關的尤拉噴射-碰撞解的解，然後接近幾乎沿著拉格朗日 L4 中心構型解的三重碰撞，但在實現完全三重碰撞之前，這三個物體沿著五條“道路”之一射出，非常接近尤拉點 2 中心構型解。然後，最終，當這個尤拉解向三重碰撞坍縮時，該解會旋出成拉格朗日 L5 等邊形狀。此外，如果我們重複相同的遊走，使其週期性，則跟隨它的解也將是週期性的。

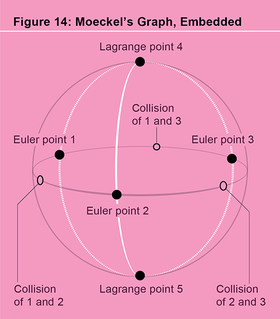
在西蒙告訴我必須存在動力學機制後不久，我意識到莫克爾的圖嵌入到形狀球體中（見圖 14）。關於這個嵌入圖的重要之處在於，它承載了帶有三個二元碰撞孔的球體的所有拓撲結構。實際上，我們可以將三次穿孔球體變形到圖上，並在這樣做時將穿孔球體中的任何環路變成圖上的遊走。為了看到這種變形，將球體想象成氣球的表面。在氣球上戳三個針孔，每個針孔位於一個二元碰撞孔處。氣球由非常柔韌的材料製成，因此我們可以拉伸我們的三個針孔，擴大它們，直到三個孔的邊緣幾乎相互接觸，並且剩餘的材料形成一條緊貼嵌入圖的帶狀物。在進行這種變形的過程中，三次穿孔球體中的任何閉合環路都會變形為這個帶狀結構中的閉合環路，並從那裡變形為莫克爾的嵌入圖上的遊走。

為了將這張圖變成關於解的定理，我需要證明，如果我將莫克爾定理保證的解投影到形狀球體上，那麼它們永遠不會偏離這個嵌入圖太遠。如果它們偏離得太遠，它們可能會纏繞在二元碰撞周圍，甚至會撞擊其中一個，從而殺死或新增一些拓撲上重要的環路，從而改變日食序列。我給莫克爾發電子郵件尋求幫助。他回覆道：“你的意思是你要強迫我讀我 20 多年前寫的論文？” 儘管如此，他還是重新投入到他的舊研究中，並證明他多年前以符號方式編碼的解的投影永遠不會偏離嵌入圖太遠。我的問題得到了解答——幾乎。

為了使他的證明奏效，莫克爾需要一點點角動量。（在這種情況下，角動量是衡量系統總“旋轉”量的指標，並且對於每個解都是恆定的。）但在我與西蒙對話之前的 17 年裡，我一直堅持要求解具有零角動量。這種堅持源於在具有給定日食序列的所有曲線中最小化作用量的解必須具有零角動量。另一方面，莫克爾需要少量角動量才能使解沿著他的圖的邊行進。數學分析中微小正量的符號是 epsilon。我們需要 epsilon 的角動量。

莫克爾的結果還有另一個問題：當他的解在尤拉點 E1、E2 和 E3 附近穿過形狀球體的赤道時，它們將在那裡在赤道上來回振盪，然後再向上移動到北極或南極，因為它們沿著相應的拉格朗日道路 L4 或 L5 接近三重碰撞。為了解釋這些振盪，取一個正整數 N，如果序列中每次出現一個數字，則稱日食序列為“N 長”，它至少連續出現 N 次。例如，序列 1112222333332222 是 3 長的，但它不是 4 長的，因為只有三個 1 連續出現。

最後，這是我們的主要定理：考慮具有小非零角動量 epsilon 和大開放範圍內的質量的三體問題。那麼存在一個大的正整數 N，它具有以下意義。如果我們選擇任何日食序列——它是 N 長的——那麼就存在一個相應的我們三體問題的解，該解恰好具有這個日食序列。如果該序列被設定為週期性的，那麼實現它的解也是週期性的。

我最初的問題呢？那裡沒有提到大的 N。我問的是每個日食序列。但我沒有告訴你我的真正問題。我真正想知道的是我是否可以實現週期曲線的任何“拓撲型別”，而不是任何日食序列。我使用日食序列作為一種方便的簡寫或編碼拓撲型別的方式，也就是說，作為一種編碼環路繞三個二元碰撞孔的纏繞模式的方式。閉合曲線的拓撲型別的日食序列表示具有冗餘：許多不同的日食序列編碼相同拓撲型別的曲線。例如，考慮拓撲型別“繞過排除二元碰撞 23 而形成的孔一次”。
日食序列 23 表示這種拓撲型別。日食序列 2223、222223 和 2333 也是如此。每當我們連續兩次穿過弧 2 時，我們可以透過拉直曲折來取消它們，使曲線在那部分保持在一個半球或另一個半球中，而不會穿過赤道（見圖 15）。實際上，我們可以取消在日食序列中出現的任何連續的相同數字對，而不會改變序列表示的閉合曲線的拓撲型別。

為了使用我們的主要定理來回答我的真正問題，請注意，透過刪除連續對，我可以確保編碼給定拓撲型別的日食序列永遠不會有兩個連續的相同型別的數字：沒有“11”或“22”或“33”。將這樣的序列稱為可容許序列。現在，取任何可容許序列，例如 123232。請允許我在寫下日食序列時使用指數表示法，因此，例如，1³ = 111。選擇一個奇數整數 n，它至少與我們的主要定理的數字 N 一樣大。將可容許序列替換為更長的序列 1ⁿ 2ⁿ 3ⁿ 2ⁿ 3ⁿ 2ⁿ 並使其週期性延續。這個更長的序列表示相同的原始選擇的拓撲型別，因為 n 是奇數。我們的定理表明，這個更長的序列由週期解實現。這個週期解表示我們原始的拓撲型別 123232。

下一步是什麼？

我們還有很多工作要做。當我大約 20 年前最初提出我的問題時，我只想要具有零角動量的解。但是越來越多的證據表明，在零角動量的情況下，我對我的問題的答案是“否”。我們有一些證據表明，即使是最簡單的非空週期序列 23 也永遠無法透過等質量、零角動量三體問題的週期解來實現。

我們在這裡提出的主要問題，即使對於角動量 epsilon，仍然是開放的，因為我們的定理只允許我們實現對於某個大的 N 來說是 N 長的序列。例如，我們不知道如何實現可容許序列，即可容許序列是沒有相同型別的連續數字的序列。

最終，我們可能並沒有更接近傳統意義上的“解決”三體問題，但我們學到了很多。我們將繼續努力——對於我們這些被它吸引的人來說，這個問題將繼續結出碩果。事實證明，從數學史上最經典的難題之一中仍然可以獲得新的見解。