想想午餐。也許是一份美味的火腿三明治。一把刀應該能幹淨利落地將火腿和兩片面包一分為二。但如果你失手了呢?糟糕——火腿現在摺疊在翻轉的盤子下面;一片面包掉在地板上,另一片粘在了天花板上。這裡有一些安慰:幾何學保證,只需一刀直線切割,也許用一把房間大小的彎刀,仍然可以完美地將你掉落的午餐分成兩半,使火腿和每片面包都恰好一半在切割線的兩側。這是因為數學的“火腿三明治定理”保證,對於任意三個(可能不對稱的)物體,在任何方向上,總會有一條直線切割可以同時將它們全部一分為二。這個事實有一些奇怪的含義,以及一些令人警醒的含義,因為它與政治中的選區劃分不公有關。
該定理可以推廣到其他維度。更數學化的措辭是,n 維空間中的 n 個物體可以被 (n – 1) 維切割同時平分。火腿三明治有點難以下嚥,但我們會讓它更容易理解。在二維紙上,你可以畫出任何你想要的兩個形狀,並且總會有一條(一維)直線將兩者完美地切成兩半。為了保證對三個物體進行均等切割,我們需要升級到三維空間,並用二維平面進行切割:將那把破壞房間的彎刀想象成一張薄紙,你將其滑入房間的兩半之間。在三維空間中,彎刀有三個自由度:你可以前後移動它穿過房間,停下來並將其旋轉到不同的角度,然後左右搖晃彎刀(就像你可能傾斜刀子以斜切胡蘿蔔而不是直線切割一樣)。
如果你能想象一個四維火腿三明治,就像數學家喜歡做的那樣,那麼你可以想象如何用三維切割來平分第四種成分。
支援科學新聞事業
如果您喜歡這篇文章,請考慮支援我們屢獲殊榮的新聞報道,方式是 訂閱。透過購買訂閱,您正在幫助確保未來能夠繼續講述關於塑造我們當今世界的發現和想法的具有影響力的故事。
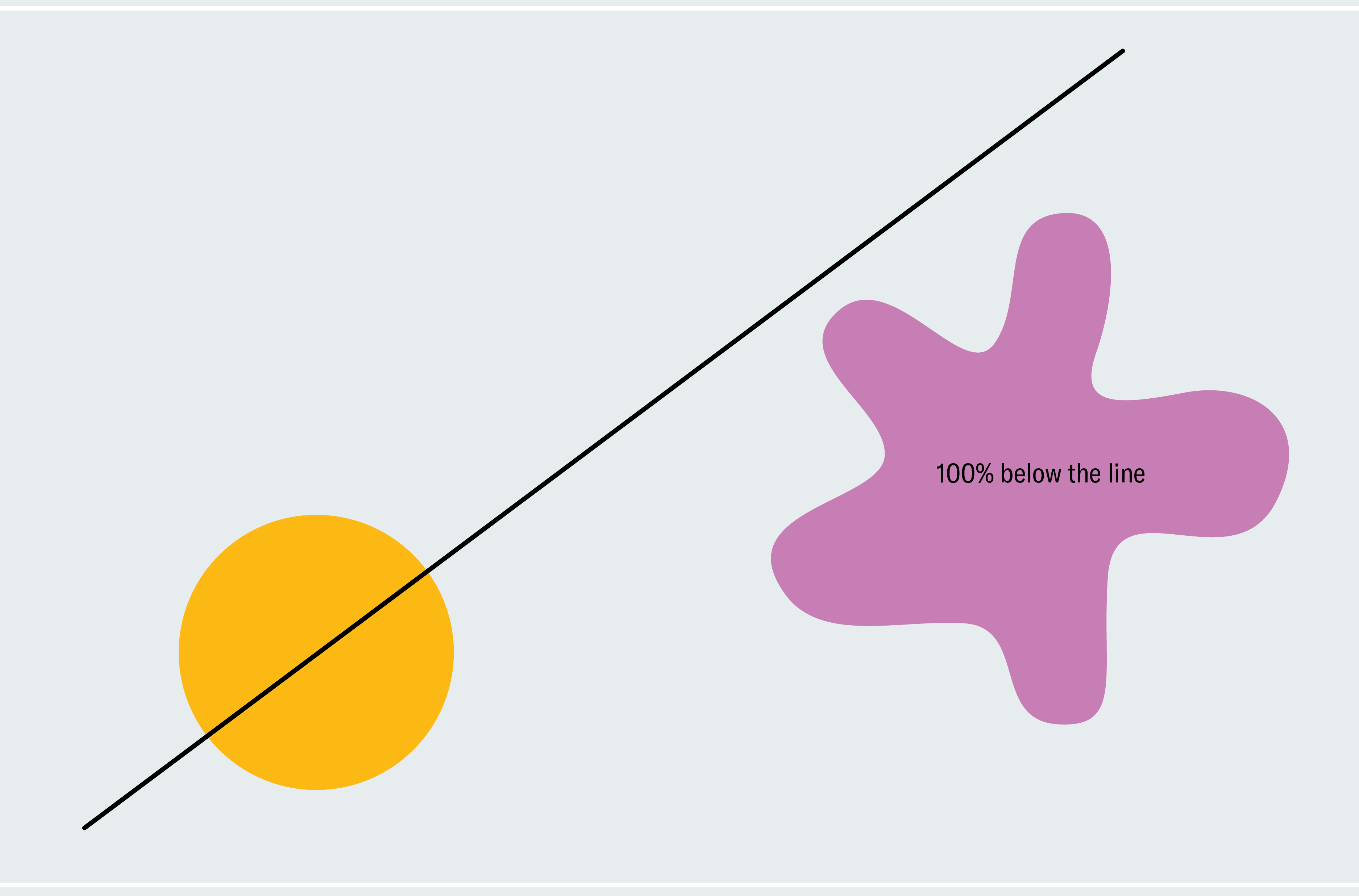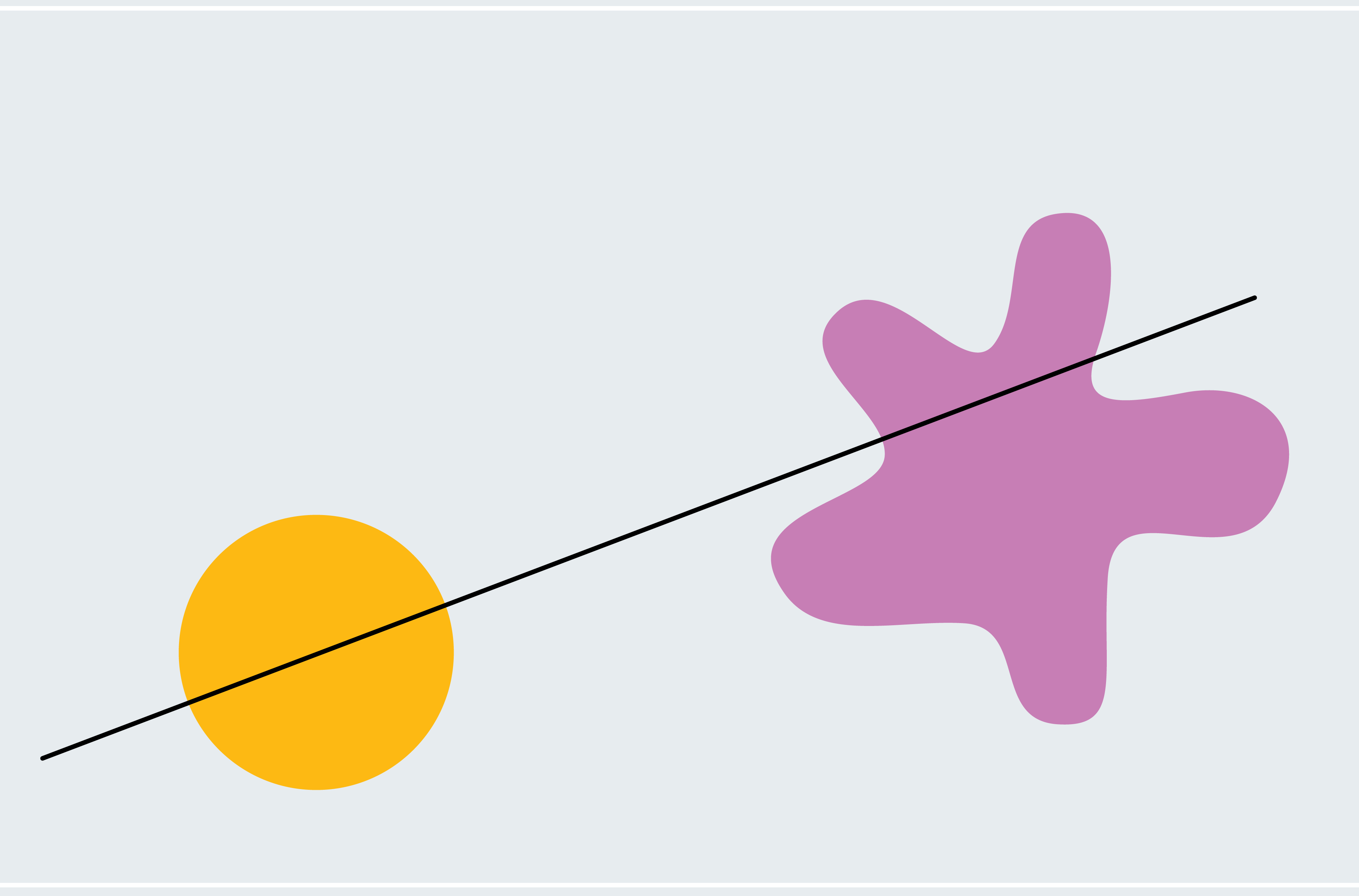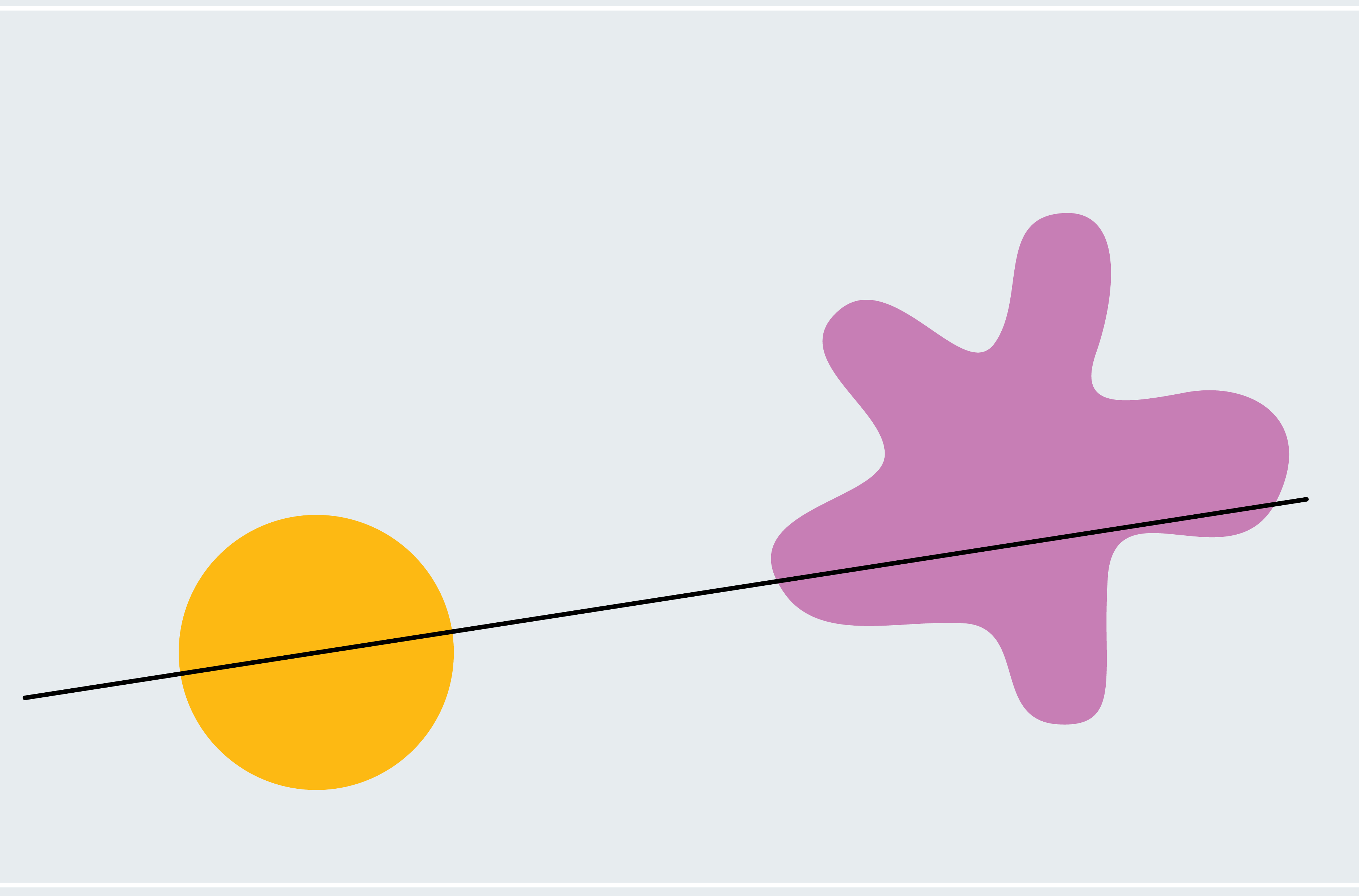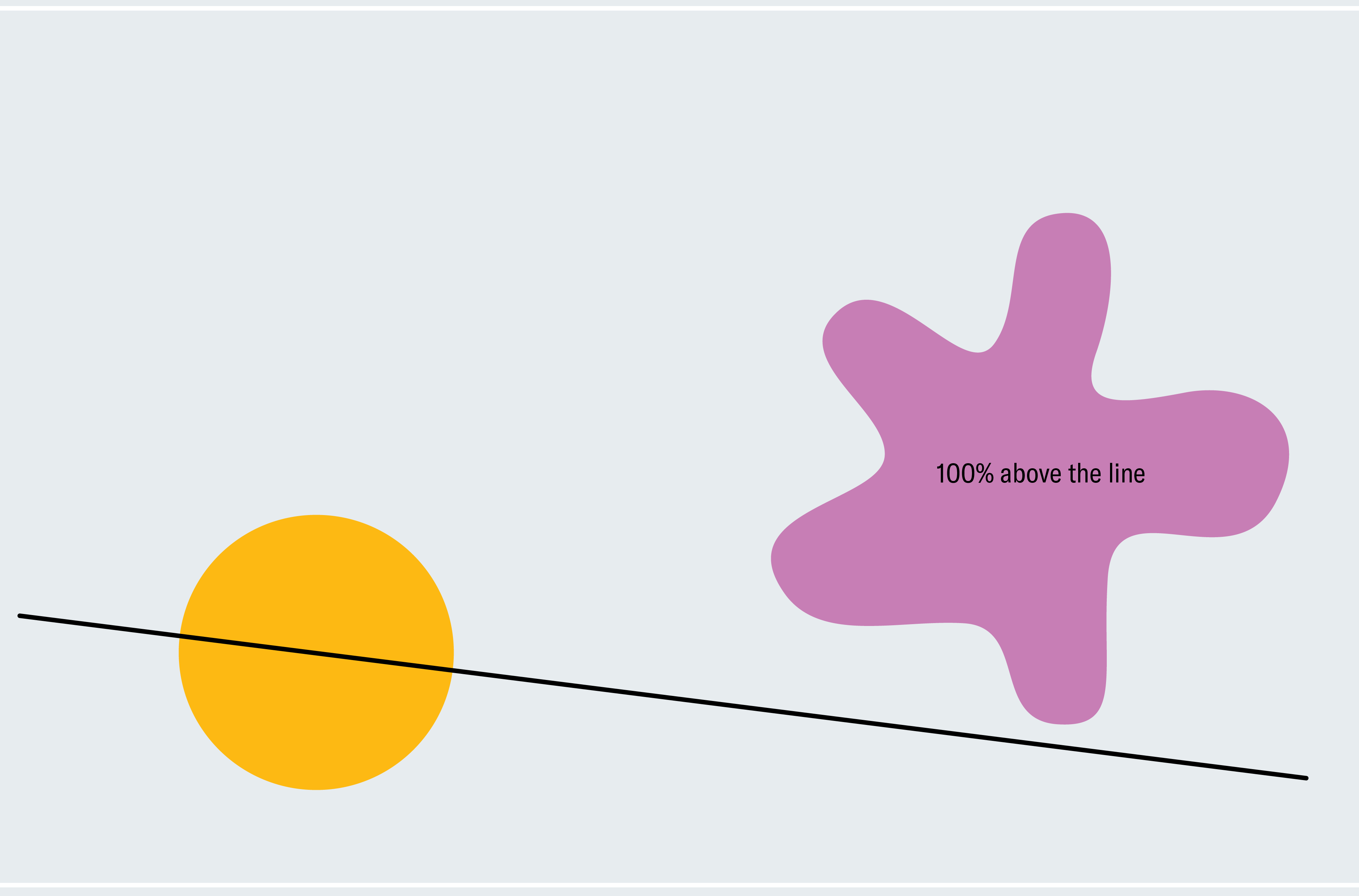
為了瞭解如何證明火腿三明治定理,請考慮一個簡化的版本:兩個二維形狀,一個圓形,另一個斑點狀。任何穿過圓心的線都會平分圓(不對稱形狀不一定有真正的中心;我們現在使用圓形是為了讓事情更簡單)。我們如何知道某條線也平分斑點狀形狀?選擇一條穿過圓心但不與斑點狀形狀相交的線。如下一欄圖形的第一幅圖所示,斑點狀形狀的 100% 位於我們的線下方。現在像風車輪一樣圍繞圓心緩慢旋轉這條線。最終,它會突破斑點狀形狀,切割越來越多的部分,然後穿過它下方,使斑點狀形狀的 0% 位於線下方。從這個過程中,我們可以推斷出一定存在一個時刻,斑點狀形狀的 50% 位於線下方。我們正在逐漸但連續地從 100% 移動到 0%,因此我們必須經過介於兩者之間的每個量,這意味著在某個時刻我們恰好達到 50%(微積分愛好者可能會將此識別為介值定理)。
這個論證證明存在一條線可以同時平分我們的形狀(儘管它沒有告訴我們這條線在哪裡)。它依賴於一個方便的事實,即每條穿過圓心的線都會平分圓,因此我們可以自由旋轉我們的線,並專注於斑點狀形狀,而無需擔心忽略圓。兩個不對稱形狀需要我們風車技術的更微妙的版本,而擴充套件到三維空間則需要更復雜的論證。
有趣的是,即使火腿和麵包被切成多塊,該定理也適用於我們的三明治。使用餅乾切割器衝壓出火腿雪人,然後將麵包切成方塊並烤成麵包丁;一個完全均等的切割將始終存在(單個雪人和麵包丁不一定會被平分,但火腿和麵包的總量將會被平分)。
阿曼達·蒙塔涅斯
將這個想法推向極致,我們可以對點做出類似的斷言。在一張紙上畫出散落的紅色和綠色點,並且總會有一條直線,其兩側分別有恰好一半的紅點和一半的綠點。這個版本需要一個小小的技術細節:恰好位於分割線上的點可以算在任一側,也可以完全不算(例如,如果你有奇數個紅點,那麼如果沒有這個注意事項,你永遠無法均勻地分割它們)。
思考一下這裡奇怪的含義。你可以畫一條橫跨美國的線,使恰好一半的國家的臭鼬和一半的 Twix 巧克力棒位於這條線的上方。雖然臭鼬和 Twix 巧克力棒實際上不是單個點,但與廣闊的美國陸地相比,它們也可以被視為點。將維度提升一級,你可以在地球上畫一個圓圈(切穿地球儀會留下圓形橫截面),其中包含世界上一半的石頭、一半的紙和一半的剪刀,或者任何其他你希望的古怪類別。
對於長期存在的選區劃分不公問題,火腿三明治定理的後果遠沒有那麼異想天開。在美國,州政府將其州劃分為選區,每個選區選舉一名美國眾議院議員。選區劃分不公是指為了政治利益而刻意劃分這些選區邊界的做法。
作為一個簡化的例子,想象一個擁有 80 人的州;其中 75% 的人(60 人)支援紫色黨,25% 的人(20 人)喜歡黃色黨。該州將被劃分為四個選區,每個選區 20 人。似乎很公平的是,其中三個選區(75%)應該是紫色,第四個應該是黃色,以便該州在國會的代表性與人口的偏好相符。然而,一位狡猾的地圖繪製者可以扭曲選區邊界,使每個選區包含 15 名傾向於紫色的選民和 5 名投票給黃色黨的人。這樣,每個選區都將是紫色多數,並且該州 100% 的代表權將來自紫色黨,而不是 75%。事實上,如果有足夠的選民,一個政黨對另一個政黨的任何百分比優勢(例如,紫色對黃色 50.01% 對 49.99%)都可以被利用來幫助該政黨贏得每個選區;只需使每個選區 50.01% 的人支援它即可。

阿曼達·蒙塔涅斯
當然,這些選區看起來非常人為。遏制選區劃分不公的一個看似顯而易見的方法是限制選區的形狀,並禁止我們在美國選舉地圖上經常看到的觸手狀怪物。事實上,許多州都施加了此類規則。雖然強制執行“正常”選區形狀似乎可以在很大程度上緩解問題,但聰明的研究人員已經應用了某個幾何定理來表明這純粹是胡說八道。
讓我們回顧一下我們的例子:總共有 80 名選民,其中 60 名紫色黨支持者和 20 名黃色黨支持者。火腿三明治定理告訴我們,無論他們如何分佈,我們都可以畫一條直線,兩側分別有恰好一半的紫色選民和一半的黃色選民(兩側各有 30 名紫色選民和 10 名黃色選民)。現在將你建立的兩個區域視為新的火腿三明治,用各自的直線將每個區域分成兩半,以便每個生成的區域包含 15 名紫色選民和 5 名黃色選民。紫色黨現在擁有與之前相同的選區劃分不公優勢(它贏得了每個選區),但生成的區域都是具有直線邊界的簡單形狀!
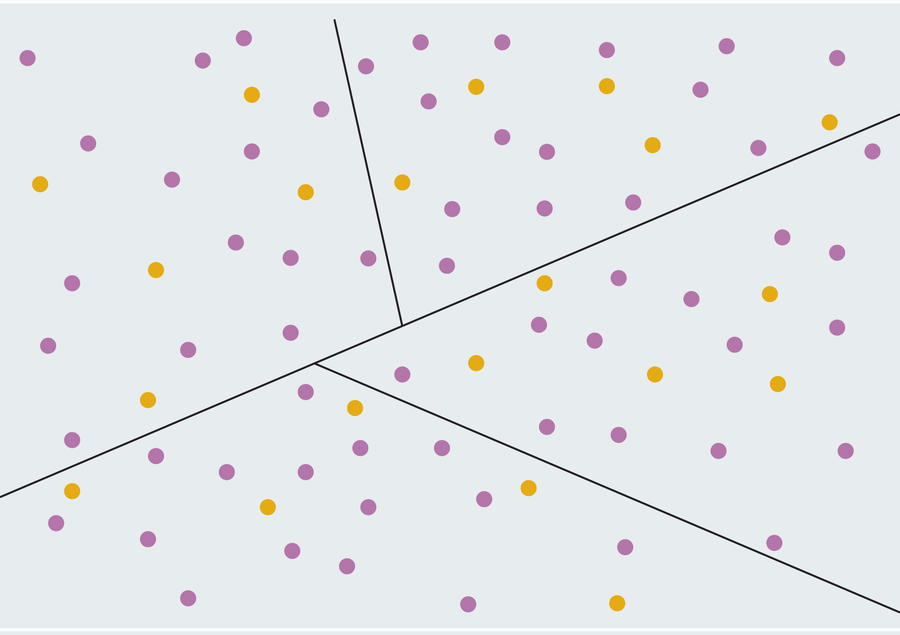
阿曼達·蒙塔涅斯
重複的火腿三明治細分將始終產生相對簡單的選區(在數學術語中,它們是凸多邊形,除非它們可能與現有州邊界共享邊界)。這意味著對國會選區形狀的基本規定可能無法排除最糟糕的選區劃分不公情況。雖然數學和政治可能看起來是遙遠的領域,但一個閒置的幾何學消遣告訴我們,針對選區劃分不公的最自然的解決方案並不能解決問題。
