乍一看,這個問題似乎荒謬地簡單。然而,專家們徒勞地尋找解決方案數十年。據數學家傑弗裡·拉加里亞斯說,數論學家角谷靜夫告訴他,在冷戰期間,“耶魯大學大約有一個月的時間,每個人都在研究這個問題,但沒有任何結果。當我在芝加哥大學提到這個問題時,也發生了類似的現象。有人開玩笑說,這個問題是減緩美國數學研究陰謀的一部分。”
考拉茲猜想——角谷靜夫描述的這個令人煩惱的難題——是那些表面上簡單但人們往往會迷失其中的問題之一。因此,經驗豐富的教授經常警告他們雄心勃勃的學生不要沉迷於此,而忽略了他們實際的研究。
這個猜想本身可以很簡單地表述出來,甚至小學生都能理解。取一個自然數。如果是奇數,乘以 3 再加 1;如果是偶數,除以 2。對結果x也以同樣的方式進行:如果x是奇數,則計算 3x + 1;否則計算 x / 2。儘可能多地重複這些指令,根據猜想,你總是會得到數字 1。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保關於塑造我們當今世界的發現和想法的具有影響力的故事的未來。
例如:如果你從 5 開始,你必須計算 5 x 3 + 1,結果是 16。因為 16 是一個偶數,你必須將它減半,得到 8。然後 8 / 2 = 4,除以 2 後得到 2——而 2 / 2 = 1。迭代計算的過程在五個步驟後將你帶到終點。
當然,你也可以繼續用 1 計算,得到 4,然後 2,然後再回到 1。計算規則將你帶入一個無法逃脫的迴圈。因此,1 被視為過程的終點。

透過迭代計算,你可以從上面的任何數字開始,最終都會達到 1。
對不同的數字進行迭代計算規則並檢視結果序列真的很有趣。如果你從 6 開始:6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1。或者 42:42 → 21 → 64 → 32 → 16 → 8 → 4 → 2 → 1。無論你從哪個數字開始,你似乎總是以 1 結尾。有些數字,例如 27,需要很長時間 (27 → 82 → 41 → 124 → 62 → 31 → 94 → 47 → 142 → 71 → 214 → 107 → 322 → 161 → 484 → 242 → 121 → 364 → 182 → 91 → 274 → ...),但到目前為止,結果始終為 1。(誠然,你必須對起始數字 27 有耐心,它需要 111 步。)
但奇怪的是,仍然沒有數學證明考拉茲猜想是正確的。這種缺失讓數學家們困惑多年。
考拉茲猜想的起源尚不確定,這就是為什麼這個假設有許多不同的名稱。專家們談到西拉古斯問題、烏拉姆問題、3n + 1 猜想、哈塞演算法或角谷問題。
德國數學家洛塔爾·考拉茲在他的數學研究期間對迭代函式產生了興趣並對其進行了研究。在 1930 年代初期,他還發表了關於該主題的專業文章,但以他的名字命名的問題的明確計算規則不在其中。在 1950 年代和 1960 年代,當數學家赫爾穆特·哈塞和角谷靜夫等人將其傳播到包括雪城大學在內的各個大學時,考拉茲猜想最終獲得了 notoriety。
就像海妖的歌聲一樣,這個看似簡單的猜想吸引了專家們。幾十年來,他們一直在尋找證據,證明在重複考拉茲過程有限次數後,你最終會得到 1。這種堅持的原因不僅僅是問題的簡單性:考拉茲猜想與其他重要的數學問題有關。例如,這種迭代函數出現在動力系統中,例如描述行星軌道的模型。該猜想還與黎曼猜想有關,黎曼猜想是數論中最古老的問題之一。
考拉茲猜想的經驗證據
在 2019 年和 2020 年,研究人員在一個協作計算機科學專案中檢查了 268 以下的所有數字,即序列中約 3 x 1020 個數字。該集合中的所有數字都滿足作為初始值的考拉茲猜想。但這並不意味著某處沒有異常值。可能存在一個起始值,在重複考拉茲過程後,產生越來越大的值,最終上升到無窮大。然而,如果從統計角度檢查這個問題,這種情況似乎不太可能。
奇數n在迭代的第一步後增加到 3n + 1,但結果不可避免地是偶數,因此在下一步中減半。在所有情況的一半中,減半產生一個奇數,因此必須再次增加到 3n + 1,然後再次獲得偶數結果。但是,如果第二步的結果再次為偶數,則在每四種情況中,你必須將新數字除以 2 兩次。在每八種情況中,你必須將其除以 2 三次,依此類推。
為了評估數字序列的長期行為,拉加里亞斯在 1985 年根據這些考慮計算了幾何平均值,並獲得了以下結果:(3/2)1/2 x (3⁄4)1/4 x (3⁄8)1/8 · ... = 3⁄4。這表明序列元素在迭代計算規則的每個步驟中平均縮小 3⁄4 的因子。因此,起始值因該過程而增長到無窮大的可能性極低。
然而,可能存在一個起始值,它以一個不是 4 → 2 → 1 的迴圈結束。該迴圈可能包含更多的數字,以至於永遠無法達到 1。
例如,如果你也允許考拉茲猜想使用負整數,則可以找到這種“非平凡”迴圈:在這種情況下,迭代計算規則不僅可以以 –2 → –1 → –2 → ... 結束,還可以以 –5 → –14 → –7 → –20 → –10 → –5 → ... 或 –17 → –50 → ... → –17 →.... 如果我們將自己限制為自然數,則迄今為止尚未知曉非平凡迴圈——但這並不意味著它們不存在。專家們現在已經能夠證明,考拉茲問題中的這種迴圈必須由 至少 1860 億個數字 組成。
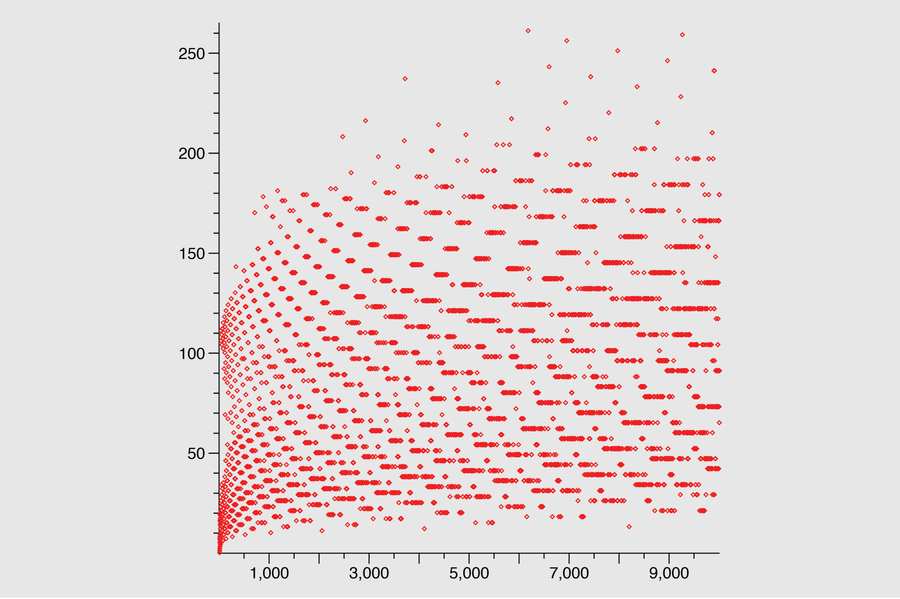
從 1 到 9,999 的所有數字的考拉茲序列的長度差異很大。
即使這聽起來不太可能,但也並非不可能。在數學中,有很多例子表明,某些定律只有在考慮多次迭代後才會失效。例如,素數定理僅對大約 10316 個數字高估了素數的數量。在那之後,素數集合低估了素數的實際數量。
考拉茲猜想也可能發生類似的情況:也許在數軸深處隱藏著一個巨大的數字,它打破了迄今為止觀察到的模式。
幾乎所有數字的證明
幾十年來,數學家們一直在尋找確鑿的證據。2019 年,加州大學洛杉磯分校的菲爾茲獎獲得者陶哲軒取得了最大的進展,當時他證明了幾乎所有自然數的起始值最終都會以接近 1 的值結束。
“幾乎所有”都有精確的數學含義:如果你隨機選擇一個自然數作為起始值,它有 100% 的機率以 1 結尾。(然而,零機率事件不一定是不可避免的事件。)陶哲軒在 2020 年的一次演講中說,這“就像在沒有實際解決考拉茲猜想的情況下儘可能接近它”。不幸的是,陶哲軒的方法無法推廣到所有數字,因為它基於統計學考慮。
所有其他方法也都走入了死衚衕。也許這意味著考拉茲猜想是錯誤的。“也許我們應該花更多的精力尋找反例,而不是我們目前所花的精力,”羅格斯大學數學家亞歷克斯·孔託羅維奇在 Veritasium YouTube 頻道上的一個影片中說。
也許考拉茲猜想將在未來幾年內被確定為真或假。但還有另一種可能性:也許這確實是一個無法用現有數學工具證明的問題。事實上,在 1987 年,已故數學家 約翰·霍頓·康威 研究了 考拉茲猜想的推廣並發現 迭代函式具有不可證明的屬性。也許這也適用於考拉茲猜想。儘管它看起來很簡單,但它可能註定永遠無法解決。
本文最初發表於《Spektrum der Wissenschaft》,並經許可轉載。
