1982 年的 SAT 考試臭名昭著地出現了一道數學題,這道題非常棘手,甚至連出題者都沒有包含正確答案。這個錯誤導致 30 萬份試卷需要重新評分,學生們成了這個棘手的硬幣旋轉悖論的受害者。
以下是這個悖論的原理:將兩枚四分之一美元硬幣平放在桌面上,使它們互相接觸。按住其中一枚硬幣使其靜止在桌面上,滾動另一枚四分之一美元硬幣繞著它轉,保持兩枚硬幣邊緣接觸且不滑動。當移動的硬幣回到其起始位置時,它已經完成了多少次完整旋轉?換句話說,在下面的圖中,喬治·華盛頓正面朝上的位置出現了多少次?如果你喜歡這樣的謎題,花一分鐘時間思考一下。
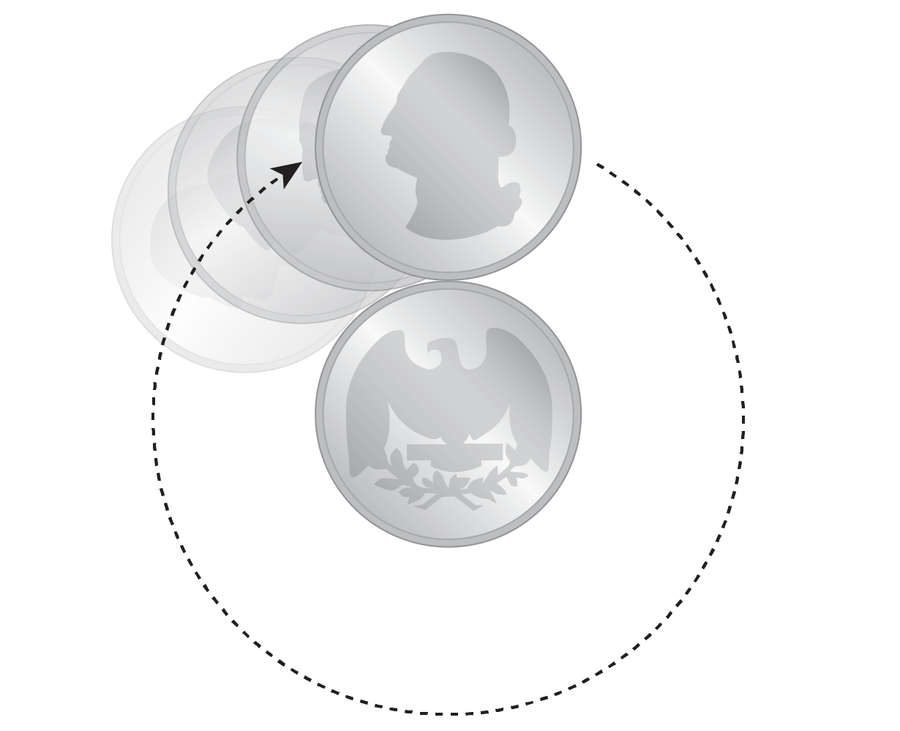
來源:阿曼達·蒙塔內斯
許多人認為喬治會完成一次完整旋轉。一枚四分之一美元硬幣的圓周長約為三英寸。因此,移動的硬幣沿著一條長度為三英寸的路徑滾動,這與它自身的圓周長相同。如果我們用一根繩子繞著一枚四分之一美元硬幣,然後沿著三英寸的路徑滾動它,同時展開繩子,那麼肯定會展開三英寸長的繩子——剛好足夠一次旋轉。
事實上,移動的硬幣在返回其原始位置時正好完成兩次完整旋轉。這種現象違背了常識。如果你覺得難以接受,我建議你親自測試一下。任何兩個大小相同的圓盤都可以。
[如需瞭解另一個數學探索,請閱讀“‘睡美人問題’為何讓數學家們徹夜難眠”]
1982 年SAT 數學部分中偷偷加入的這個問題的版本略有不同:中心圓盤比繞著它滾動的圓盤更大。以下是該問題的一個版本,措辭略有修改,使其更清晰:
圓 B 的半徑是圓 A 半徑的三倍。從圖中所示位置開始,圓 A 繞圓 B 滾動。當圓 A 返回其起點時,它將完成多少次旋轉?
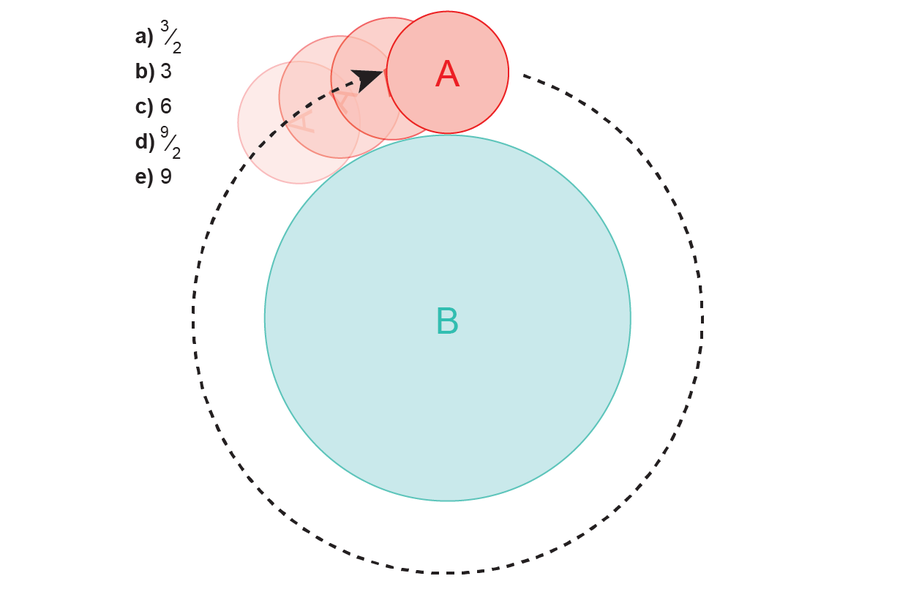
來源:阿曼達·蒙塔內斯
這看起來是否很熟悉?在這裡,我們被告知較大圓的半徑是較小圓半徑的三倍。這意味著兩個圓的圓周長也具有相同的比例:B 的周長是 A 的三倍。人們很容易推斷出,較小的圓可以“展開”自身三次來包圍較大的圓。因此,“3”是 SAT 考試中預期的多項選擇答案。事實上,圓 A 在其行程中完成了四次旋轉——同樣,比直覺預期的多一次旋轉。這個悖論遠遠超出了命題人的認知,以至於選項中沒有提供“4”這個答案,因此即使是最聰明的學生也被迫提交了錯誤的答案。在參加包含該問題的考試的 30 萬名學生中,有三名向大學理事會報告了這個問題,並且每份試卷都必須重新評分。
那麼,為什麼會多出一次旋轉呢?上面導致我們誤入歧途的方法確實包含一些道理。沿著三英寸直線路徑滾動一枚四分之一美元硬幣只會涉及一次旋轉。同樣,一個小圓在一個長度為其直徑三倍的直線上滾動會旋轉三次。因此,路徑的圓形形狀以某種方式引起了自身的旋轉。為了理解原因,想象一下繞著一顆微小的罌粟種子滾動一枚四分之一美元硬幣。即使繞種子的長度可以忽略不計,喬治也會旋轉一次。因此,旋轉有兩個來源:一個來自沿著路徑滾動(路徑越長,旋轉次數越多),另一個來自繞物體旋轉,無論物體大小如何,它都會貢獻一次旋轉。
另一個有用的視角來自想象繞著正方形滾動一枚四分之一美元硬幣。正方形的每條邊都是直線段,喬治的頭像每三英寸長度會旋轉一次,但是當你到達一個角時,四分之一美元硬幣將不得不旋轉更多才能透過那個角。(同樣,如果難以想象,請親自嘗試一下。)事實證明,角落處的額外旋轉正好是 90 度,這導致當硬幣穿過正方形的所有四個角並返回起點時,總共旋轉了一整圈(360 度)。類似地,繞著三角形滾動將需要在每個角處旋轉 120 度。
這種效應可以放大到天體。眾所周知,月球有遠端,並且總是將同一面朝向我們地球人。許多人錯誤地認為,月球不變的面貌意味著它一定不像地球那樣繞其軸自轉。但是,如果月球在繞軌道執行時不自轉,那麼我們會從地球上的某些地方看到它的遠端。你可以用自己的拳頭來演示這一點——保持一個拳頭靜止,然後讓另一個拳頭繞著它旋轉,而沒有任何自轉。站在你靜止的指關節上的人會看到不同時間 orbiting 拳頭的不同景象。為了永遠隱藏其背面,月球必須在完成一次軌道執行時旋轉一次。(軌道時間和自轉時間之間的這種完美一致性並非天文巧合,而是一個稱為潮汐鎖定現象的例子。我們也在迴避我們的相對論參考系,向阿爾伯特·愛因斯坦致歉。)對於硬幣和 SAT 問題,我們看到旋轉有兩個來源:一些來自沿著任何路徑的“直線”滾動,另一個來自繞物體旋轉的額外旋轉。月球不做任何直線滾動。如果地球是平的,月球將在其上方滑行而不會滾動。因此,月球的單次旋轉完全是因為它圍繞非常球形的地球公轉。
如果你有一個太陽系的鳥瞰圖,你會在典型的一年中看到地球完成多少次旋轉?許多人會說是 365 次,但再一次,他們的答案會比正確答案少一次:366 次。(請注意,這與閏年無關,閏年是完全不同的事情。)人類將一天定義為太陽返回到天空同一位置所需的時間。總是讓太陽在中午正上方是很方便的。但是,當地球完成一次旋轉時,太陽實際上還沒有完全回到天空中的位置。讓我們重新審視 SAT 圖表,看看發生了什麼——這次我們將在小圓上標記一個固定點,並觀察當小圓繞大圓滾動時該點會發生什麼變化:
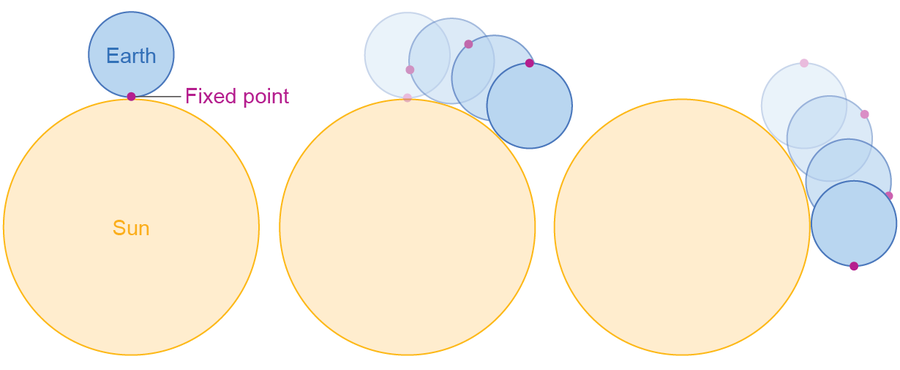
來源:阿曼達·蒙塔內斯
將大圓想象成太陽,小圓想象成地球(未按比例),點想象成我們星球上的一個固定點。在第一張圖中,點直接盯著太陽。現在正好是中午。在最後一張圖中,小圓完成了一次完整旋轉(點再次指向下方),但請注意,對於站在該點的人來說,現在不是中午。小圓需要向前移動一點點超過一次旋轉,才能使該點再次親吻大圓。同樣,儘管地球在 23 小時 56 分鐘內完成一次旋轉(這被稱為恆星日),但太陽需要多花四分鐘才能返回到天空中的正上方位置,從而產生我們定義的 24 小時制的一天。在 365 天的過程中,每天多出的這四分鐘旋轉加起來就是額外的一次旋轉。
感謝您與我們一起滾動瀏覽硬幣、測試錯誤和行星運動之旅——這足以讓任何人頭暈目眩。
編者注(2023 年 6 月 24 日):這篇文章在釋出後經過編輯,將“月球的陰暗面”的說法更改為“月球的遠端”。
