黎曼猜想是數論中最重要的未解問題——如果不是整個數學界的話。它已經困擾專家們超過160年。這個問題既出現在數學家大衛·希爾伯特1900年的開創性演講中,也出現在一個世紀後提出的“千禧年難題”中。解決這個問題的人將贏得一百萬美元的獎金。
但是,黎曼猜想是一塊難啃的骨頭。儘管付出了數十年的努力,眾多專家的興趣和現金獎勵,但進展甚微。現在,麻省理工學院的數學家拉里·格思和牛津大學的詹姆斯·梅納德在預印本伺服器arXiv.org上釋出了一項轟動性的新發現。德國波恩大學的數論學家瓦倫丁·布洛默說,在這篇論文中,“作者改進了一個看似50多年來無法逾越的結果。”
其他專家也同意。數學家和菲爾茲獎得主陶哲軒在Mastodon上寫道,這項工作是“一個了不起的突破”,“儘管距離完全解決這個猜想還很遙遠。”
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
黎曼猜想關係到自然數的基本組成部分:質數,即大於1且只能被1和自身整除的值。例如,2、3、5、7、11、13等等。*
每個其他數字,例如15,都可以清楚地分解為質數的乘積:15 = 3 x 5。問題是質數似乎沒有遵循簡單的模式,而是隨機地出現在自然數中。十九世紀德國數學家伯恩哈德·黎曼提出了一種處理這種特性的方法,解釋了質數如何在數軸上分佈——至少從統計學的角度來看。
數字的元素週期表
證明這個猜想將為數學家提供不亞於一種“數字的元素週期表”的東西。正如物質的基本組成部分(如夸克、電子和光子)幫助我們理解宇宙和我們的世界一樣,質數也發揮著重要的作用,不僅在數論中,而且在幾乎所有數學領域中。
現在有許多定理是基於黎曼猜想的。證明這個猜想也將證明許多其他定理——這是解決這個頑固問題的又一個動力。
對質數的興趣可以追溯到數千年前。早在公元前300年,歐幾里得就證明了質數的數量是無限的。儘管人們對質數的興趣持續存在,但直到18世紀,關於這些基本組成部分才取得任何進一步的重大發現。
作為一名15歲的少年,物理學家卡爾·弗里德里希·高斯意識到,質數的數量沿著數軸遞減。他所謂的質數定理(直到100年後才被證明)指出,在從0到n的區間內,大約出現n/ln(n)個質數。換句話說,質數定理為數學家提供了一種估計質數在數軸上的典型分佈的方法。
然而,質數的精確數量可能與定理給出的估計值不同。例如:根據質數定理,在1到100之間的區間內,大約有100/ln(100) ≈ 22個質數。但實際上有25個。因此,存在3的偏差。這就是黎曼猜想的用武之地。這個猜想為數學家提供了一種估計偏差的方法。更具體地說,它指出這種偏差不會變得任意大,而必須最多與n的平方根成比例,n是所考慮區間的長度。
因此,黎曼猜想並沒有準確預測質數位於何處,而是假定它們在數軸上的出現遵循一定的規則。根據黎曼猜想,質數的密度根據質數定理而降低,並且質數根據這個密度均勻分佈。這意味著沒有大片區域完全沒有質數,而另一些區域則充滿了質數。
您也可以透過思考房間空氣中分子的分佈來想象這個想法:地板上的總體密度略高於天花板,但粒子——遵循這種密度分佈——仍然均勻分散,並且任何地方都沒有真空。
一個奇怪的聯絡
黎曼在1859年以一篇簡短的六頁出版物(他唯一對數論領域的貢獻)中提出了以他名字命名的猜想。然而,乍一看,他的工作與質數幾乎沒有關係。
他處理了一個特定的函式,即所謂的zeta函式ζ(s),這是一個無限長的和,它將自然數的倒數值加起來,這些自然數被提高到s的冪

甚至在黎曼的工作之前,專家們就知道這樣的zeta函式與質數有關。因此,zeta函式也可以表示為所有質數p的函式,如下所示
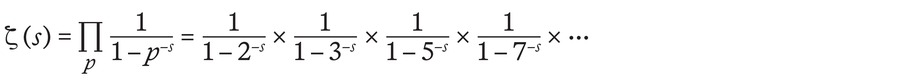
當黎曼不僅使用s的實數值,而且還使用複數時,他認識到這種與質數聯絡的全部意義。這些數字包含實部和負數的根,即所謂的虛部。
您可以將複數想象成一個二維結構。它們不是在數軸上標記一個點,而是位於平面上。x座標對應於實部,y座標對應於虛部
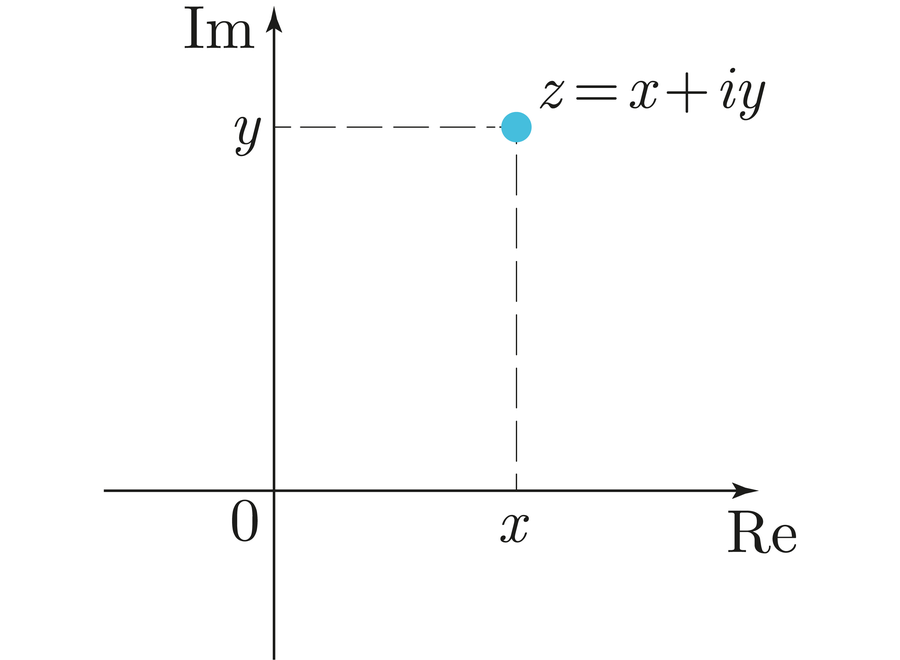
Никита Воробьев/Wikimedia
黎曼研究的復zeta函式可以視覺化為平面上方的景觀。事實證明,在群山和山谷之間,有一些點在質數關係中起著重要作用。這些點是zeta函式變為零的點(所謂的零點),景觀降至海平面,可以這麼說。
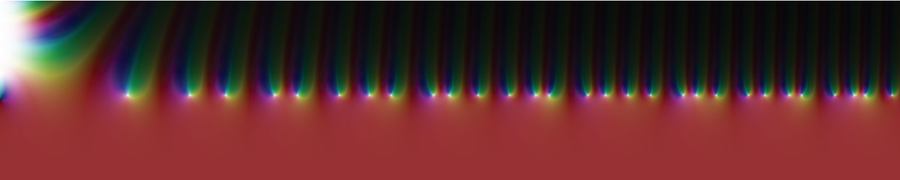
顏色代表復zeta函式的值,白色點表示其零點。
Jan Homann/Wikimedia
黎曼很快發現,如果實部大於1,則zeta函式沒有零點。這意味著直線x = 1右側的景觀區域永遠不會降至海平面。zeta函式的零點對於實部的負值也是已知的。它們位於實軸上,x = –2、–4、–6等等。但是,真正讓黎曼以及此後所有數學家感興趣的是“臨界帶”0 ≤ x ≤ 1中zeta函式的零點。
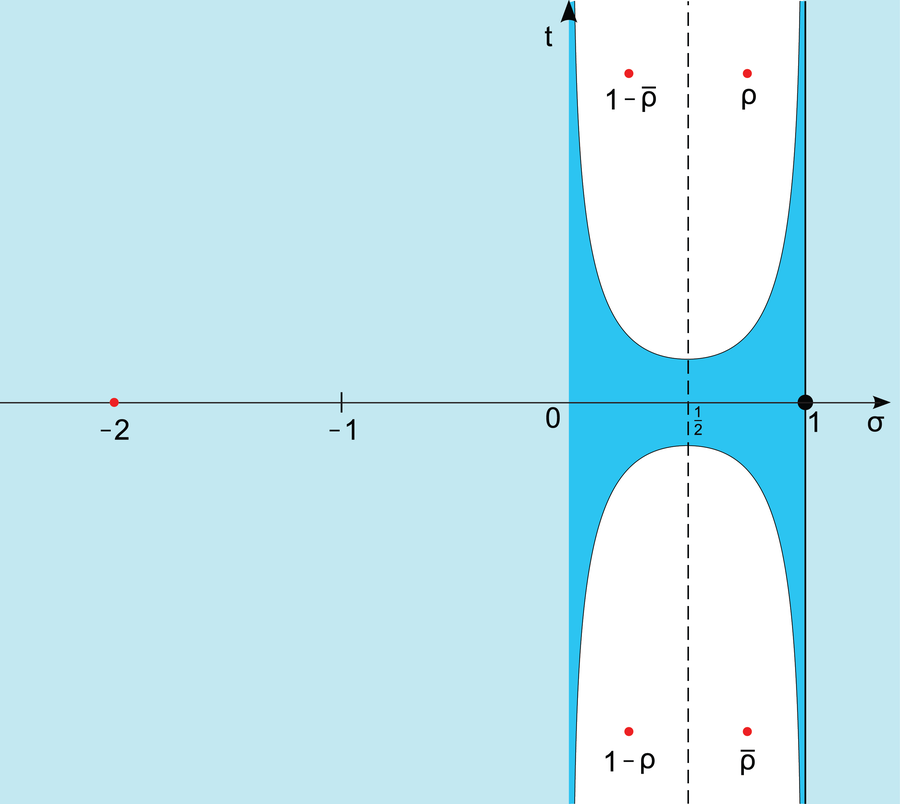
在臨界帶(深藍色)中,黎曼zeta函式可能具有“非平凡”零點。黎曼猜想指出,這些零點僅位於直線 x = 1/2(虛線)上。
LoStrangolatore/Wikimedia (CC BY-SA 3.0)
黎曼知道zeta函式在臨界帶內有無限個零點。但有趣的是,所有零點似乎都位於直線x = 1/2上。因此,黎曼假設臨界帶內zeta函式的所有零點的實部都為x = 1/2。這個陳述實際上是理解質數分佈的關鍵。如果正確,那麼質數在數軸上的位置永遠不會與質數集偏差太大。
尋找零點
迄今為止,數十億甚至數百億個zeta函式零點已經被檢查過——超過1013個——並且全部都位於直線x = 1/2上。
但僅憑這一點還不是有效的證明。您只需要找到一個偏離此方案的零點即可證偽黎曼猜想。因此,我們正在尋找一個證明,明確表明在臨界帶中,x = 1/2之外沒有零點。
到目前為止,這樣的證明仍然遙不可及,因此研究人員採取了不同的方法。他們試圖證明,在直線x = 1/2之外,最多隻有一定數量N的零點。希望是將N減少到某個點N = 0,從而證明黎曼猜想。不幸的是,這條路徑也被證明極其困難。1940年,數學家阿爾伯特·英厄姆能夠證明,在0.75 ≤ x ≤ 1之間,最多有y3/5+c個零點,其虛部最多為y,其中c是0到9之間的常數。
在隨後的80年中,這種估計幾乎沒有改進。上一次值得注意的進展來自數學家馬丁·赫胥黎,在1972年。“這限制了我們在解析數論中做很多事情,”陶哲軒在他的社交媒體帖子中寫道。例如,如果您想將質數定理應用於[x, x + xθ]型別的短區間,您會被英厄姆的估計限制在 θ > 1/6。
然而,如果黎曼猜想是正確的,那麼質數定理適用於任何區間(或 θ = 0),無論區間有多小(因為 [x, x + xθ] = [x, x + 1] 適用於 θ = 0)。
現在,在2022年被授予著名菲爾茲獎的梅納德和格思成功地首次顯著改進了英厄姆的估計。根據他們的工作,在0.75 ≤ x ≤ 1範圍內,zeta函式最多有y(13/25)+c個零點,其虛部最多為y。這到底意味著什麼?布洛默解釋說:“作者在定量意義上表明,黎曼zeta函式的零點離臨界直線越遠就越稀有。換句話說,對黎曼猜想的可能違反情況越糟糕,它們就越少發生。”
陶哲軒寫道:“這傳播到解析數論中的許多相應改進。” 這使得可以縮小質數定理適用的區間的尺寸。該定理適用於[x, x + x2/15],因此 θ > 1/6 = 0.166... 變為 θ > 2⁄15 = 0.133...
為了取得這一進展,梅納德和格思最初為他們的結果使用了傅立葉分析中的眾所周知的方法。這些技術類似於將聲音分解為其泛音的技術。“最初的幾個步驟是標準的,許多解析數論學家,包括我自己,都曾嘗試突破英厄姆界限,都會認出它們,”陶哲軒解釋說。然而,從那裡開始,梅納德和格思“做了一些聰明且出乎意料的操作,”陶哲軒寫道。
布洛默表示贊同。“這項工作提供了一整套新的想法,正如作者正確指出的那樣,這些想法可能可以應用於其他問題。從研究的角度來看,這是這項工作最決定性的貢獻,”他說。
因此,即使梅納德和格思尚未解決黎曼猜想,他們至少為解決這個有160年曆史的難題提供了新的思路。誰知道呢——也許他們的努力掌握著最終破解這個猜想的關鍵。
本文最初發表於Spektrum der Wissenschaft,並經許可轉載。
*編者注(2024年7月9日):這句話在釋出後進行了編輯,以更好地澄清質數不包括1。
