啤酒冰鎮後飲用最佳,事實證明,數學可以對此有所幫助。巴西聖若昂-德爾-雷聯邦大學的克勞迪奧·德·卡斯特羅·佩萊格里尼最近著手製定一個方程式,以確定啤酒杯的最佳形狀,從而使飲料保持美味的冰鎮狀態——換句話說,他正在尋找一種可以防止杯中液體吸收熱量的玻璃杯。
最簡單的方法是找到一個表面積相對於其體積儘可能小的容器。這是因為來自玻璃杯周圍環境的熱量會滲透到玻璃杯的表面。表面越小,進入的熱量就越少,啤酒保持令人愉悅的涼爽的時間就越長。早在古代,學者們就認識到,在二維情況下,圓形提供了周長與面積的最小比率。這一發現也適用於三維:與體積相比,球體的表面積最小。
但是球形啤酒杯會很不方便。更重要的是,佩萊格里尼對靜態情況不感興趣,在靜態情況下,你將啤酒放在玻璃杯中,然後看著液體變暖。“這個過程非常簡單:點一杯啤酒,服務員送來,上酒,飲用。重複。”他在描述這項研究的預印本論文中寫道,該論文於 10 月份釋出到 arXiv.org 伺服器。這意味著玻璃杯內的液位會發生變化,與環境接觸的表面也會發生變化。(隨著玻璃杯中的啤酒被喝掉更多,其更多的表面會接觸到周圍的空氣。)
支援科學新聞事業
如果您喜歡這篇文章,請考慮支援我們屢獲殊榮的新聞事業,方式是 訂閱。透過購買訂閱,您將有助於確保未來能夠繼續報道有關塑造我們當今世界的發現和思想的具有影響力的故事。
佩萊格里尼從玻璃杯形狀的一些約束條件開始。它應該由一個絕緣的平底座組成,底座要足夠大,以使玻璃杯能夠直立。此外,玻璃杯應該是對稱的,因此其形狀由旋轉體表示,即透過將二維形狀繞 x 軸或 y 軸旋轉 360 度而建立的三維形狀。為了確定最佳啤酒杯形狀,佩萊格里尼調整了定義旋轉體的二維形狀。在 2 月份 arXiv.org 上詳細介紹的早期預印本分析中,他以這種方式描述了最佳玻璃杯形狀,但最可行的容器體積超過兩升,而最大的玻璃杯體積超過 100 升。
接下來,佩萊格里尼旨在設計一個實用的啤酒杯。但他必須做一些簡化。他假設底座可以完美地隔熱。(實際上,厚玻璃底座和杯墊的使用有所幫助,但完美的絕緣是不可能的。)他還假設啤酒的溫度在液體中處處相同,並且飲料具有均勻的密度,這對於過濾後的品種來說基本上是正確的。佩萊格里尼忽略了啤酒泡沫作為可能的絕緣層。最後,他還忽略了人手向玻璃杯的熱傳遞,僅研究了環境溫度的影響。“在最關鍵的情況下,例如在 [38 攝氏度] 的海灘上颳風的日子裡,只需 3 分鐘就可能足以(再次基於個人經驗,反覆驗證)使啤酒變得無法飲用,”佩萊格里尼寫道。
最佳啤酒杯的公式
基於這些假設,研究人員建立了一個方程,描述了啤酒溫度隨時間的變化。這是一個微分方程,意味著該公式包含一個導數:一個函式,顯示了變化率(在本例中為溫度)相對於變數的變化率,在這種情況下,變數是啤酒杯的形狀

這裡,T 是啤酒溫度,TU 是環境溫度,cp 是比熱容(物質升溫的難易程度),ρ 是密度,V 是體積,Atot 是啤酒的暴露表面(包括側面和上部圓形表面),hCV 是對流換熱係數,表示其導熱能力。使用這個公式,佩萊格里尼計算出了四個確保啤酒儘可能緩慢降溫的技巧。
最好的情況是,您應該在涼爽的地方享用啤酒,以便 TU 儘可能低。
如果您使用陶瓷等更具絕緣性的材料代替玻璃,則導熱係數會降低。
總的來說,佩萊格里尼指出,厚厚的泡沫層可以隔離啤酒,並防止二氧化碳過快流失。此外,應避免風和氣流,因為這些會導致強制對流,與此處考慮的自然對流相比,強制對流在熱傳遞中起著更大的作用。
所有這些技巧通常只能透過移動到不同的位置來遵循。如果您舒適地坐在酒吧裡,您將暴露於當地的條件,因此,如果酒吧從一開始就使用形狀經過最佳化的玻璃杯以實現最小的熱交換,那將是非常受歡迎的。劇透:情況並非如此。
啤酒香檳杯
啤酒杯的形狀包含在上述方程中的商 Atot⁄V 中。該數字越小,溫度變化就越小。這就是佩萊格里尼專注於最小化 Atot⁄V 值的原因。
在學校裡,數學家們瞭解到,這種最佳化任務可以透過導數來解決。例如,要找到拋物線 f(x) = x2 + 3x + 2 的頂點,該函式是從 x 匯出的,結果設定為零:0 = 2x + 3。這意味著頂點可以在 x = –1.5 處找到。
佩萊格里尼以完全相同的方式進行:他匯出了商 Atot/V,將其設定為零,然後使用旋轉體的屬性推匯出了最佳啤酒杯形狀的函式。根據這個,完美啤酒杯的半徑 r 作為高度 h 的函式,由以下公式給出

C 是一個常數,Rb 是玻璃杯底座的半徑。該公式表明,玻璃杯的杯口應該很大,並且玻璃杯應該向底部變窄,類似於許多常見的啤酒杯。然而,現實世界中玻璃杯的半徑並非總是逐漸變小——它們通常具有彎曲的 S 形,從側面看是這樣。這使它們與完美的啤酒杯區分開來。
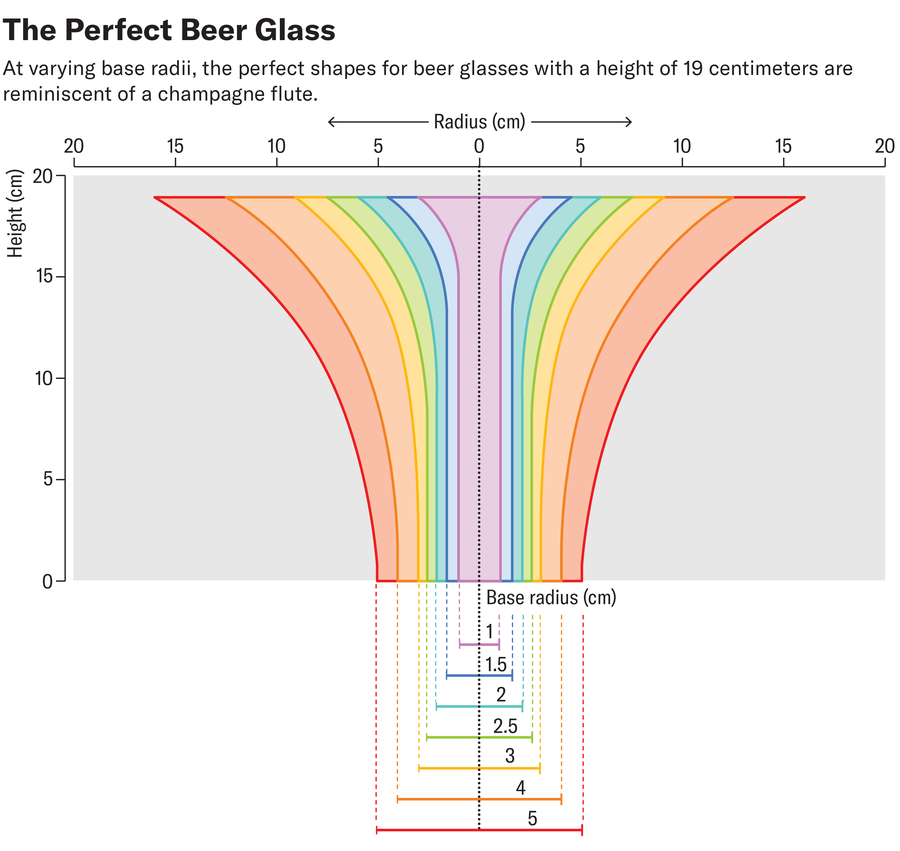
克勞迪奧·德·卡斯特羅·佩萊格里尼,由阿曼達·蒙塔涅斯修改和重新設計;來源:克勞迪奧·C·佩萊格里尼的“最佳化啤酒杯形狀以最大限度地減少熱傳遞——新結果”。預印本於 2024 年 10 月 15 日釋出至 https://arxiv.org/abs/2410.12043
最佳玻璃杯的確切形狀取決於玻璃杯底座的半徑和常數 C,常數 C 由玻璃杯的高度等因素決定。佩萊格里尼首先計算了高度為 19 釐米的不同底座半徑的玻璃杯的最佳形狀。由此產生的形狀讓人聯想到香檳杯。
然後,工程師調整了完美玻璃杯的引數,以適應不同型別的啤酒杯,例如英制品脫杯、美式品脫杯或小麥啤酒杯,這些啤酒杯在英國廣泛使用。為此,佩萊格里尼將相應的底座半徑和高度輸入到他的公式中,以計算最佳形狀。
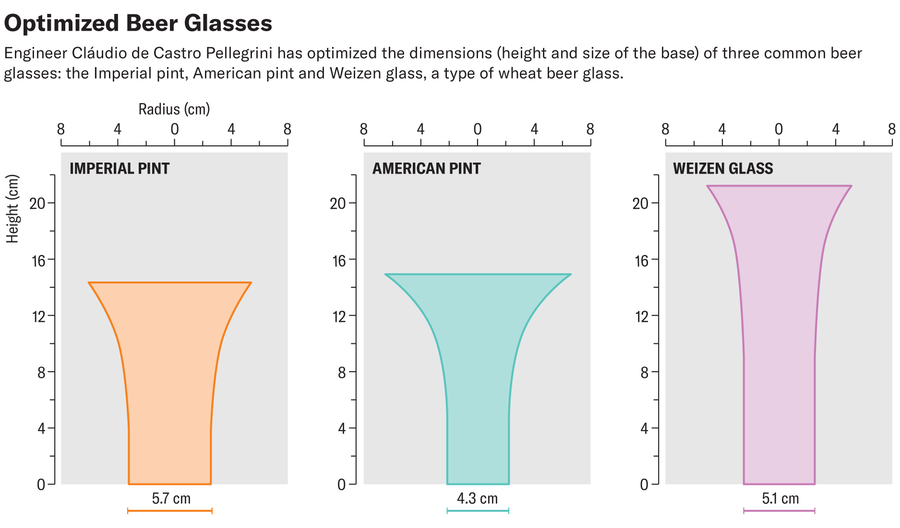
克勞迪奧·德·卡斯特羅·佩萊格里尼,由阿曼達·蒙塔涅斯修改和重新設計;來源:克勞迪奧·C·佩萊格里尼的“最佳化啤酒杯形狀以最大限度地減少熱傳遞——新結果”。預印本於 2024 年 10 月 15 日釋出至 https://arxiv.org/abs/2410.12043
在這裡,對於所有型別,大致形狀看起來也相同,並且讓人聯想到香檳杯。但即使是非最佳玻璃杯也有一些好處,佩萊格里尼在預印本中寫道。雖然在巴西廣泛使用的 Nadir Figueiredo 玻璃杯遠非最佳形狀,但它們在某些方面仍然是為熱傳遞而完美設計的:因為它們容納的啤酒量相對較小,人們通常會比啤酒明顯變暖之前更快地喝完啤酒。
本文最初發表於《明鏡》週刊,並經許可轉載。
