當克雷數學研究所為七個未解決的數學難題分別設立了100萬美元的獎金時,他們可能低估了其中一個條目的價值——而且低估了很多。如果數學家們能夠以正確的方式解決計算機科學的“P與NP”問題,其成果的價值可能遠遠超過100萬美元。他們將破解大多數線上安全系統,徹底革新科學,甚至實際上解決所謂的千禧年難題中的其他六個,所有這些難題都是在2000年選定的。無論怎樣強調計算機科學中最重要的未解難題的利害關係都不為過,計算機科學就是其中之一。
P與NP問題關注的是尋找問題的解決方案和驗證問題的解決方案之間明顯的非對稱性。例如,假設您正在計劃一次世界巡迴宣傳您的新書。您開啟Priceline並開始測試路線,但您嘗試的每一條路線都超出了您的旅行預算總額。不幸的是,隨著您全球巡演的城市數量增加,要檢查的可能路線數量呈指數級增長,即使對於計算機來說,詳盡地搜尋每種情況也是不可行的。但是當您抱怨時,您的圖書經紀人回覆了一個航班解決方案序列。您可以透過簡單地檢查它是否到達每個城市並計算票價與預算限制進行比較,來輕鬆驗證他們的路線是否在預算之內。請注意此處的非對稱性:找到解決方案很難,但驗證解決方案很容易。
P與NP問題詢問這種非對稱性是真實的還是幻覺。如果您可以有效地驗證問題的解決方案,這是否意味著您也可以有效地找到解決方案?找到解決方案應該比驗證解決方案更難,這似乎是顯而易見的。但是研究人員以前也感到驚訝。問題看起來可能同樣困難,但當您深入挖掘時,您會發現某些問題的捷徑,並在其他問題上遇到瓶頸。也許一個巧妙的捷徑可以避開圖書巡迴宣傳問題中數萬億條潛在路線的搜尋。例如,如果您改為想找到兩個特定偏遠機場之間且在預算範圍內的航班序列,您也可能會對要檢查的可能路線數量之多而束手無策。事實上,這個問題包含足夠的結構,計算機科學家已經為此開發了一種快速程式(或演算法),可以繞過詳盡搜尋的需求。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保關於塑造我們當今世界的發現和想法的具有影響力的故事的未來。
P與NP問題在我們所看到的計算世界中隨處可見,遠遠超出了我們的旅行場景的具體細節——以至於它已經成為我們理解計算的聖盃的象徵。然而,每次嘗試解決它都只會進一步揭示證明它是否成立是多麼的困難。
在理論計算機科學的子領域,稱為複雜性理論,研究人員試圖確定計算機可以多麼容易地解決各種型別的問題。P代表他們可以有效解決的問題類別,例如在電子表格中對一列數字進行排序或在地圖上查詢兩個地址之間的最短路徑。相比之下,NP代表計算機可以有效驗證解決方案的問題類別。我們的圖書巡迴宣傳問題,學術界稱之為旅行推銷員問題,屬於NP,因為我們有一個有效的程式來驗證代理商的解決方案是否有效。
請注意,NP實際上包含P作為子集,因為徹底解決問題是驗證問題解決方案的一種方法。例如,您將如何驗證27 × 89 = 2,403?您將自己解決乘法問題並檢查您的答案是否與聲稱的答案匹配。我們通常用簡單的維恩圖來描述P和NP之間的關係
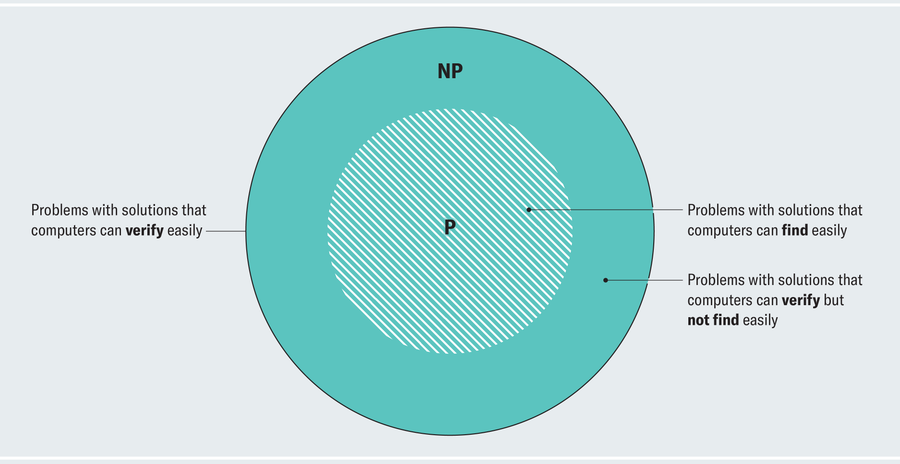
來源:阿曼達·蒙塔內斯
NP內部但不屬於P的區域包含無法透過任何已知的有效演算法解決的問題。(理論計算機科學家對“有效”使用了可以辯論的技術定義,但它可以作為通俗概念的有用替代。)但我們不知道這是因為此類演算法不存在,還是我們只是沒有鼓起創造力來發現它們。這種表示法提供了另一種表達P與NP問題的方式:這些類實際上是不同的嗎?還是維恩圖會坍縮成一個圓圈?所有NP問題都可以有效解決嗎?
以下是一些NP中的問題示例,目前尚不清楚它們是否屬於P
給定一個社交網路,是否存在一個指定規模的群體,其中所有人都彼此是朋友?
給定各種各樣的要運輸的箱子,是否可以將它們全部裝入指定數量的卡車中?
給定一個數獨(推廣到 n × n 謎題網格),它是否有解決方案?
給定一張地圖,是否可以使用僅三種顏色對國家進行著色,以使沒有兩個相鄰的國家是相同的顏色?
問問自己,您將如何驗證對某些列出的問題的建議解決方案,然後您將如何找到解決方案。請注意,近似解決方案或解決小例項(我們大多數人都可以解決9 × 9的數獨)是不夠的。要符合解決問題的資格,演算法需要為所有例項(包括非常大的例項)找到精確的解決方案。
每個問題都可以透過暴力搜尋來解決(例如,嘗試地圖的每種可能的著色,看看是否有任何一種可行),但是要嘗試的情況數量隨著問題規模的增加呈指數級增長。這意味著,如果我們稱問題的規模為 n (例如,地圖上的國家數量或要裝入卡車的箱子數量),那麼要檢查的情況數量看起來像 2n。世界上最快的超級計算機也無法對抗指數級增長。即使當 n 等於300時,按照現代資料標準來看,這只是一個很小的輸入規模,但 2300 超過了可觀測宇宙中原子的數量。在點選此類演算法的“開始”按鈕後,您的計算機將顯示一個旋轉的彩色小球,它的壽命將超過您和您的後代。
數千個其他問題也屬於我們的列表。從細胞生物學到博弈論,P與NP問題觸及科學和工業的遙遠角落。如果P = NP(也就是說,我們的維恩圖溶解成一個圓圈,並且我們獲得了這些看似困難的問題的快速演算法),那麼整個數字經濟將變得容易崩潰。這是因為諸如您的信用卡號和密碼之類的許多加密技術透過將私人資訊隱藏在計算難度大的問題背後而起作用,只有當您知道金鑰時,這些問題才可能變得容易解決。我們所知的線上安全建立在未經證實的數學假設之上,如果P = NP,這些假設就會崩潰。
令人驚訝的是,我們甚至可以將數學本身視為一個NP問題,因為我們可以程式設計計算機來有效地驗證證明。事實上,傳奇數學家庫爾特·哥德爾在1956年給他的同事約翰·馮·諾伊曼的信中首次提出了P與NP問題。哥德爾觀察到P = NP“將產生極其重要的後果。也就是說,這顯然意味著……數學家關於是非問題的腦力勞動可以完全被機器取代。”
如果您是一位擔心自己工作的數學家,請放心,大多數專家認為P不等於NP。除了有時解決方案應該比驗證更難找到的直覺之外,數千個最難的NP問題(目前尚不清楚它們是否屬於P)一直未能在不同的領域得到解決,它們閃耀著名譽和財富的誘惑,但還沒有人為一個問題設計出有效的演算法。
當然,直覺和缺乏反例並不構成證明。要證明P與NP不同,您必須以某種方式排除所有最難的NP問題的潛在演算法,這項任務似乎超出了當前數學技術的範圍。事實上,該領域透過證明所謂的障礙定理來應對,這些定理表明,解決P與NP問題的所有有希望的證明策略類別都無法成功。我們不僅未能找到證明,而且我們也不知道最終的證明可能是什麼樣子。
