你最喜歡的數字是什麼?對於許多人來說,它可能是一個無理數,例如 pi (π)、尤拉數 (e) 或 2 的平方根。即使在自然數(正整數)中,也有些值感覺很重要,因為我們在各種各樣的語境中遇到它們:七個小矮人、七宗罪、不吉利的數字 13——以及 42,這個數字因道格拉斯·亞當斯 1979 年的小說《銀河系漫遊指南》而廣為人知。
那麼像 1,729 這樣更大的值呢?這個數字當然看起來並不特別令人興奮。它不是素數,也不是 2 的冪次方,也不是某個其他數字的平方。這些數字似乎沒有遵循任何明顯的模式。這就是 數學家戈弗雷·哈羅德·哈代 在 1918 年於倫敦乘坐計程車時,看到車牌號為 1729 時的想法。當時,他正要去醫院拜訪他生病的同事 斯里尼瓦薩·拉馬努金,當他到達時,他提到了這個“無聊”的計程車號碼。他告訴拉馬努金,他希望這不是一個壞兆頭。拉馬努金立即反駁了他的朋友:“這是一個非常有趣的數字;它是可以用兩種不同的方式表示為兩個立方和的最小數字。”
你可能會想:有沒有什麼數字在某種程度上不是有趣的?這個問題很快就導致了一個悖論:如果存在一個值 n 沒有令人興奮的屬性,那麼這個事實本身就使它變得特別。但是,有一種方法可以相當客觀地確定數字的有趣屬性——令數學家們大為驚訝的是,2009 年的研究表明,自然數可以分為兩個界限分明的陣營:令人興奮的值和無聊的值。
一個全面的數字序列百科全書為研究這兩個對立的類別提供了一種手段。數學家尼爾·斯隆在 20 世紀 60 年代寫博士論文時就有了編寫這樣一部彙編的想法。他必須計算一種稱為樹網路的圖形中值的高度,並遇到一個數字序列:0、1、8、78、944 ... 他不知道如何準確計算這個序列中的數字,並且他想知道他的同事是否已經遇到過類似的序列。但是,與對數或公式不同,沒有數字序列的登錄檔。因此,10 年後,斯隆出版了他的第一部百科全書《整數序列手冊》,其中包含約 2,400 個序列,這些序列也被證明在進行某些計算時很有用。這本書受到了巨大的讚譽。“有舊約、新約和整數序列手冊,”一位熱情的讀者寫道,據斯隆說。
在隨後的幾年裡,斯隆的數字序列目錄變得越來越大。1995 年,這位數學家與他的同事西蒙·普勞夫共同出版了《整數序列百科全書》,其中包含約 5,500 個條目。此後,該列表一直在增長。截至 2023 年 3 月,線上整數序列百科全書 (OEIS) 包含超過 360,000 個條目。任何人都可以提交——他們只需要說明序列是如何生成的以及為什麼有趣,並提供示例解釋前幾個項。然後,審稿人檢查條目,如果符合他們的標準,它就會被髮布。
除了眾所周知的序列,例如素數(2、3、5、7、11 ...)、2 的冪次方(2、4、8、16、32 ...)和斐波那契數列(1、1、2、3、5、8、13 ...),OEIS 目錄還包含一些奇異的條目,例如用 n 個二乘四螺柱樂高積木建造穩定塔的方法數量(1、24、1,560、119,580、10,166,403 ...)和“懶惰的餐飲服務員序列”(1、2、4、7、11、16、22、29 ...),這是用 n 刀切一塊餡餅可以切成的最大塊數。該集合旨在客觀地彙編所有序列,這使其對於研究數字的流行度非常有用——數字在列表中出現的頻率越高,它就越有趣。
至少這就是運營法語科學部落格 Dr. Goulu 的菲利普·古格列爾梅蒂的邏輯。在一篇文章中,古格列爾梅蒂回憶起一位數學老師聲稱 1,548 是一個任意數字,沒有任何特殊屬性。事實上,這個數字在 OEIS 目錄中出現了 326 次。一個例子:它顯示為“寬度為 n 的迴圈宇宙中規則 110 細胞自動機中單個單元的最終週期”。哈代也錯了,當他說出租車號碼 1729 很無聊時:1,729 在資料庫中出現了 918 次(並且也經常出現在電視節目《飛出個未來》中)。
古格列爾梅蒂開始尋找真正無聊的數字:那些在 OEIS 目錄中很少出現,或者像 20,067 一樣,根本沒有出現的數字。截至今年三月,20,067 是未出現在 OEIS 任何儲存的數字序列中的最小數字。(這是因為資料庫僅儲存數字序列的前 180 個左右的字元;否則,每個數字都會出現在 OEIS 的正整數列表中。)20,068 只有六個條目。
來源:Philippe Guglielmetti(圖形),由 Jen Christiansen 重新設計
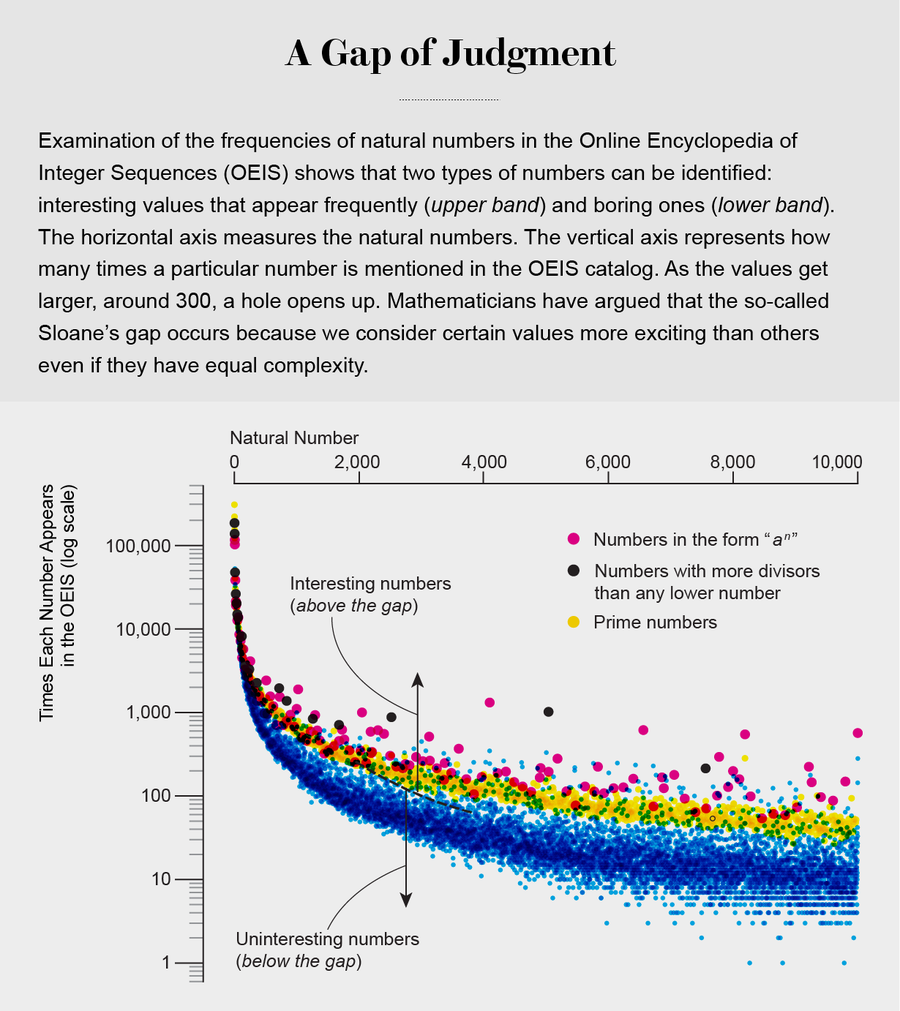
古格列爾梅蒂繼續以圖形方式繪製無聊數字的序列。他發現了一片點的雲,形狀為一條向較大值傾斜的寬曲線。這並不令人驚訝,因為 OEIS 目錄中僅儲存了序列的前幾項。然而,令人驚訝的是,該曲線由兩個帶組成,這兩個帶之間有一個清晰可見的間隙。這個間隙意味著任何給定的自然數在 OEIS 資料庫中要麼出現得特別頻繁,要麼極其罕見。
古格列爾梅蒂對這個結果很著迷,他轉向法國里爾大學的數學家讓-保羅·德拉海耶,他定期為《Pour la Science》(《大眾科學》的法語合作出版物)撰稿。他想知道專家是否已經研究過這種現象。他們沒有,所以德拉海耶與他在里爾的同事尼古拉斯·高夫裡特和劍橋大學的赫克託·澤尼爾一起研究了這個課題。他們使用了演算法資訊理論的結果,該理論透過描述表示式的最短演算法的長度來衡量表達式的複雜性。例如,一個任意的五位數,如 47,934,比 16,384 (214) 更難描述(“數字序列 4、7、9、3、4”)。根據資訊理論的一個定理,具有許多屬性的數字通常也具有較低的複雜性。也就是說,在 OEIS 目錄中頻繁出現的值最有可能易於描述。德拉海耶、高夫裡特和澤尼爾能夠證明,資訊理論預測的自然數複雜性軌跡與古格列爾梅蒂曲線中顯示的軌跡相似。但這並不能解釋該曲線中被稱為斯隆間隙的巨大空洞,該間隙以尼爾·斯隆的名字命名。
這三位數學家認為,該間隙源於社會因素,例如對某些數字的偏好。為了證實這一點,他們運行了所謂的蒙特卡洛模擬:他們設計了一個將自然數對映到其他自然數的函式——並且以這樣一種方式進行,即小數字的輸出頻率高於大數字。研究人員將隨機值輸入到函式中,並根據其頻率繪製結果圖。最終產品是一條模糊的、傾斜的曲線,類似於 OEIS 目錄中的資料。與資訊理論分析一樣,沒有間隙的蹤跡。
為了更好地理解為什麼會出現間隙,必須檢視哪些數字屬於哪個帶。對於大約 300 以內的值,斯隆間隙不是很明顯。只有對於更大的數字,間隙才會顯著開啟:大約 300 到 10,000 之間的所有數字中,有 18% 位於“有趣”帶中,其餘 82% 是“無聊”值。事實證明,有趣帶包括約 95.2% 的平方數和 99.7% 的素數,以及 39% 的具有多個素因子的數字。這三類幾乎佔了有趣帶的 88%。其餘部分由具有顯著屬性的值組成,例如 1,111 或公式 2n + 1 和 2n– 1。
根據資訊理論,應該特別感興趣的數字是那些複雜性較低的數字,這意味著它們易於表達。但是,如果數學家認為某些值比複雜度相等的其他值更令人興奮,那麼這可能會導致斯隆間隙,正如德拉海耶、高夫裡特和澤尼爾所論證的那樣。例如:從資訊理論的角度來看,2n + 1 和 2n + 2 的複雜度相同,但只有第一個公式的值在有趣帶中。這些值出現在許多不同的語境中,因為它們允許研究素數。
那麼,有趣和無聊數字的分裂似乎是我們做出的判斷的結果,例如重視素數。如果你想在被問到你最喜歡的數字是什麼時給出一個真正有創意的答案,你總是可以說“20,067”。
編者注(2023 年 9 月 26 日):在釋出後編輯了“判斷的差距”框,以更正圖表的 y 軸。

