當你點選簡訊上的“傳送”鍵時,很容易想象這條資訊會直接從你的手機傳到你朋友的手機上。但事實上,它通常會經過蜂窩網路或網際網路的長途跋涉,而這兩種網路都依賴於集中的基礎設施,這些基礎設施可能會因自然災害而受損,或被壓迫性政府關閉。出於對國家監視或干預的擔憂,香港精通技術的抗議者避開了網際網路,轉而使用 FireChat 和 Bridgefy 等軟體,在附近的手機之間直接傳送訊息。
這些應用程式可以讓資訊在手機之間靜默跳躍,最終將傳送者與接收者連線起來——只有使用者才能檢視訊息。這種連結手機的集合,被稱為網狀網路或移動自組網,實現了一種靈活和去中心化的通訊模式。但是,為了讓任何兩部手機進行通訊,它們需要透過一系列其他手機連線起來。在香港各地分散的人群中,有多少人需要透過同一個網狀網路連線,我們才能確信可以實現跨城通訊?

圖片來源:Jen Christiansen(圖表);Wee People 字型,ProPublica 和 Alberto Cairo(人物繪圖)
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保未來能夠繼續產出關於塑造我們當今世界的發現和想法的有影響力的報道。
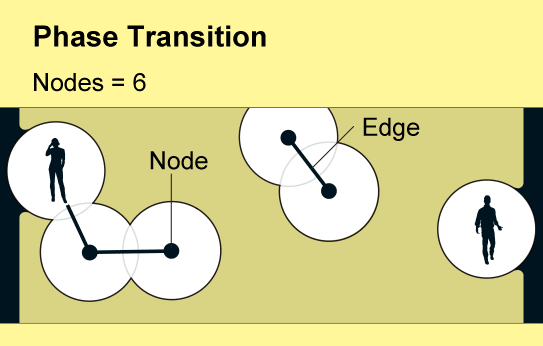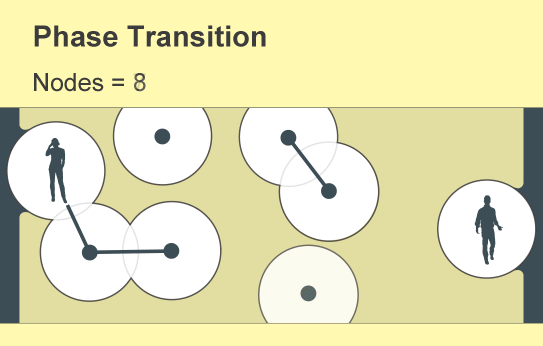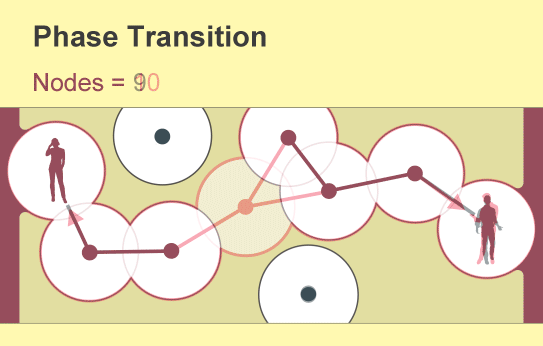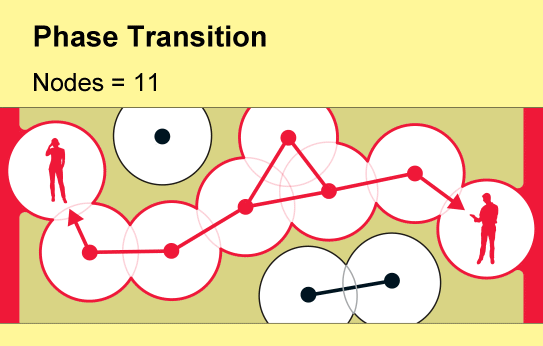
一個名為滲流理論的數學分支提供了一個令人驚訝的答案:僅僅少數人就可以產生巨大的影響。當用戶加入新網路時,孤立的連線手機群會慢慢出現。但是,當用戶密度超過一個臨界且急劇的閾值時,東西或南北方向的完全通訊就會突然出現。科學家將網路連通性的這種快速變化描述為相變——這個概念也用於解釋材料狀態的突然變化,例如冰的融化或水的沸騰。
圖片來源:Jen Christiansen(圖表);Wee People 字型,ProPublica 和 Alberto Cairo(人物繪圖)
滲流理論研究在網路中隨機建立或移除連結的後果,數學家將網路概念化為節點(用點表示)與“邊”(線)的集合。每個節點代表一個物件,例如手機或人,邊代表它們兩者之間的特定關係。滲流理論的基本見解可以追溯到 20 世紀 50 年代,即隨著網路中連結數量的逐漸增加,一個全球互聯的節點叢集將突然出現。
科學家們努力回答的問題是:何時?對於任何給定的網路,相當於冰融化的零攝氏度或水沸騰的 100 攝氏度是什麼?一個模因在何時會走紅?一種產品在何時會主導市場?地震在何時開始?手機網路在何時實現完全連線?或者疾病在何時變成全球大流行?滲流理論為所有這些轉變提供了深刻的見解。
數學家通常研究理想化的網路——幾何對稱且無限延伸——因為這些網路適合理論計算。無限網路通常是唯一具有真正急劇相變的網路。現實世界的網路範圍有限,通常很混亂,並且需要具有挑戰性的計算——但是它們也具有轉變,儘管轉變更為平緩。隨著世界透過複雜連結層變得日益互聯,這些連結層傳輸人員,透過電網為他們提供能源,或透過社交媒體將他們連線起來——有時還在他們之間傳播疾病——滲流理論變得越來越相關。
突然到位
1957 年,英國數學家西蒙·拉爾夫·布羅德本特和約翰·邁克爾·哈默斯利首次將滲流理論定義為一個純粹的數學問題。他們從化學中抽象出對滲流的研究,化學描述了流體過濾透過材料的過程,例如石油滲過多孔岩石或水過濾過研磨咖啡。岩層滲流網路由其結構中的小孔組成,表示為節點,以及允許流體在它們之間流動的通道或裂縫,表示為邊。毫不奇怪,石油在裂縫更多的岩石中流動得更遠。布羅德本特和哈默斯利使用滲流理論預測,在理想化的岩石中,當裂縫密度超過某個閾值時,石油將從僅在小區域流動轉變為突然滲透幾乎整個岩石。
地質學家使用滲流理論的一個版本來研究裂縫岩石中簇的大小,這與透過水力壓裂法提取石油和地震的發生有關。為了模擬地震,地震學家建立了與觀測到的裂縫尺度和密度相匹配的滲流網路,然後透過調整裂縫連線起來的機率來考慮應力。隨著應力和連結的增加,簇會擴充套件,直到突然且不可預測地爆發地震。滲流過程的修改版本允許裂縫癒合和再次斷裂,以模擬餘震或長期變化。
滲流理論還闡明瞭更小尺度上的物理和化學過程,例如聚合,即稱為單體的小而簡單的分子結合在一起形成稱為聚合物的較大簇的過程。在滲流理論框架中,每個單體充當一個節點,兩個相鄰單體可能自發形成一個鍵或邊。如果它們連線的可能性增加,系統最終將達到滲流閾值,並且將出現一個巨大的、連線的聚合物。這個過程就是導致溶於水的明膠粉末凝固並形成果凍的原因。
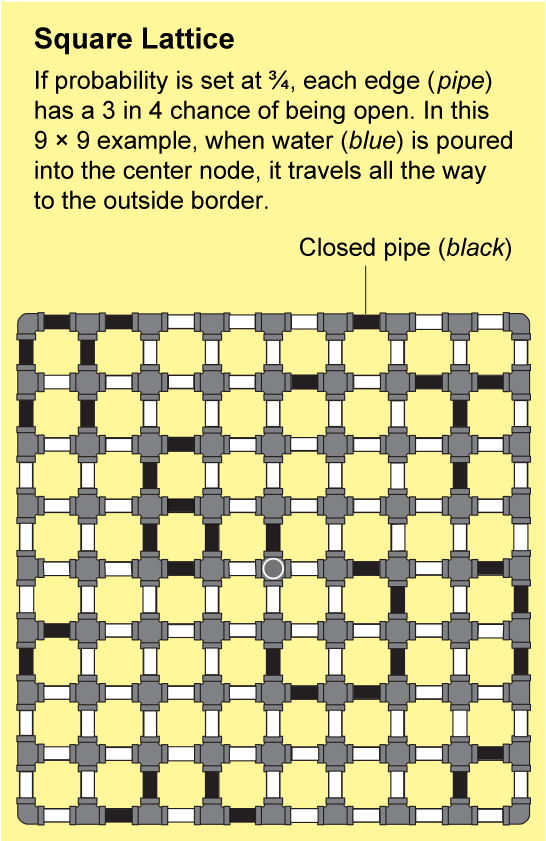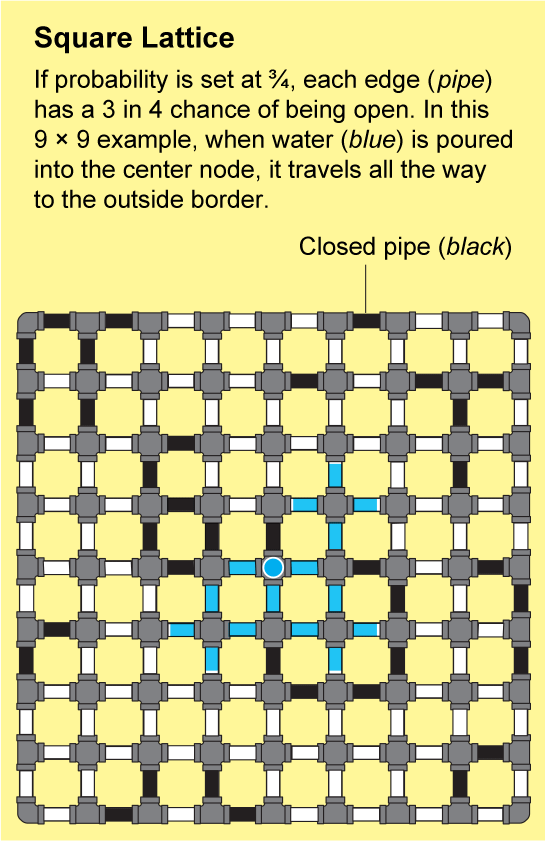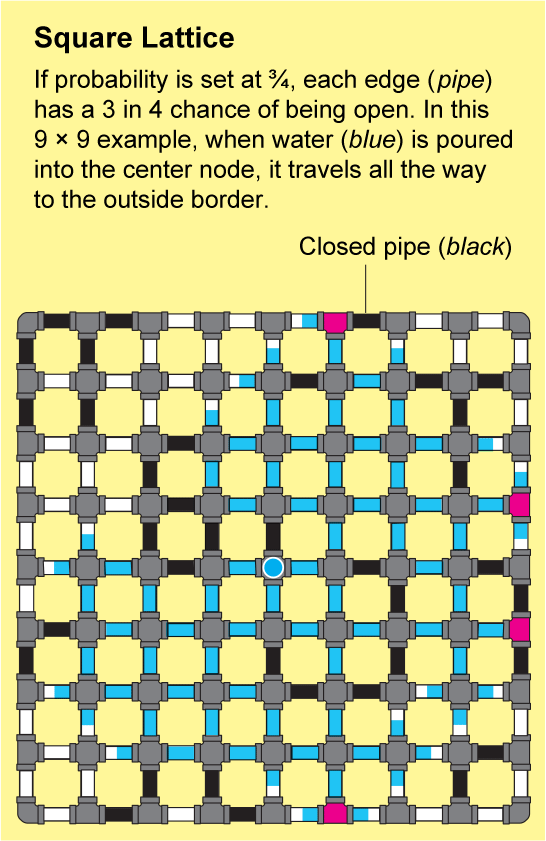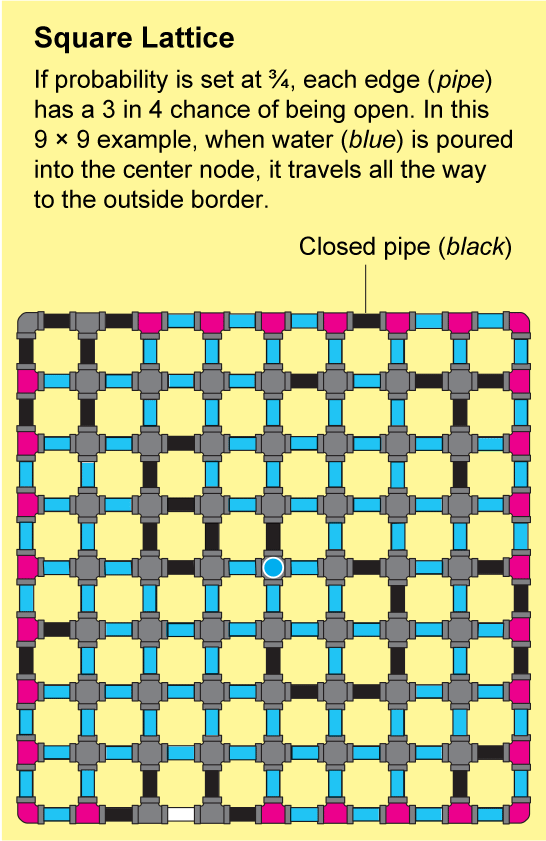
裂縫岩石或連線聚合物中的網路非常複雜。幾乎不可能精確地描述它們的結構,但是布羅德本特和哈默斯利表明,它們可以用易於分析的重複模式來近似。最簡單的例子是正方晶格,它看起來像一張無盡的方格紙:節點排列成網格,並透過四條邊連線到它們的鄰居。
為了瞭解流體如何在晶格中傳播,假設方格紙上的每條小邊都是一根管道,管道要麼開啟,要麼關閉。我們可以透過拋擲一面標有“開啟”和另一面標有“關閉”的硬幣來確定每根管道的狀態。由此產生的開啟和關閉管道的景觀將是一個隨機網路,並且它將具有一些“開啟”的簇,其中所有節點都透過一系列開啟的管道連線。如果你將水倒入這樣一個簇中的任何節點,水將透過開啟的管道流到該簇中的所有其他節點。
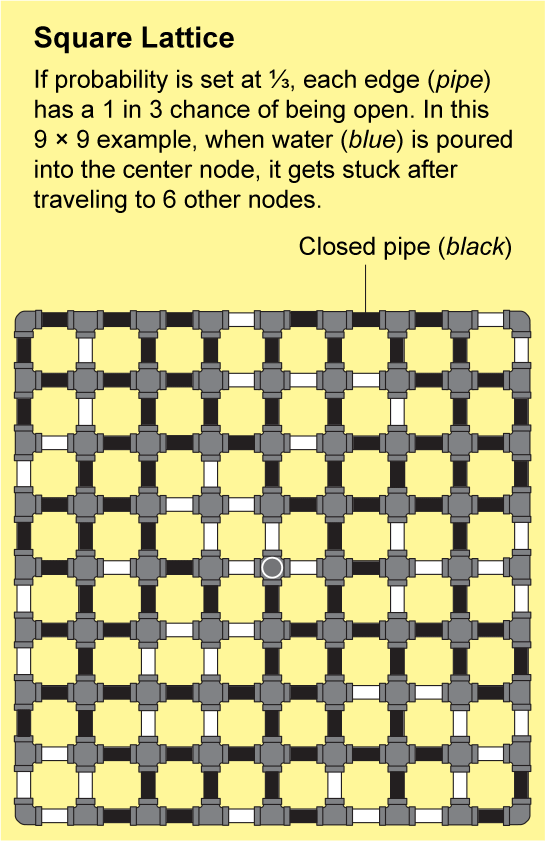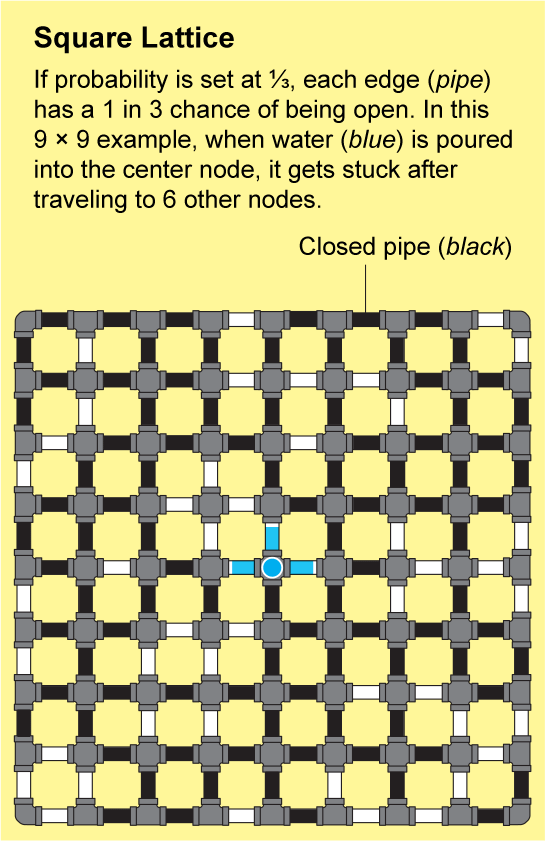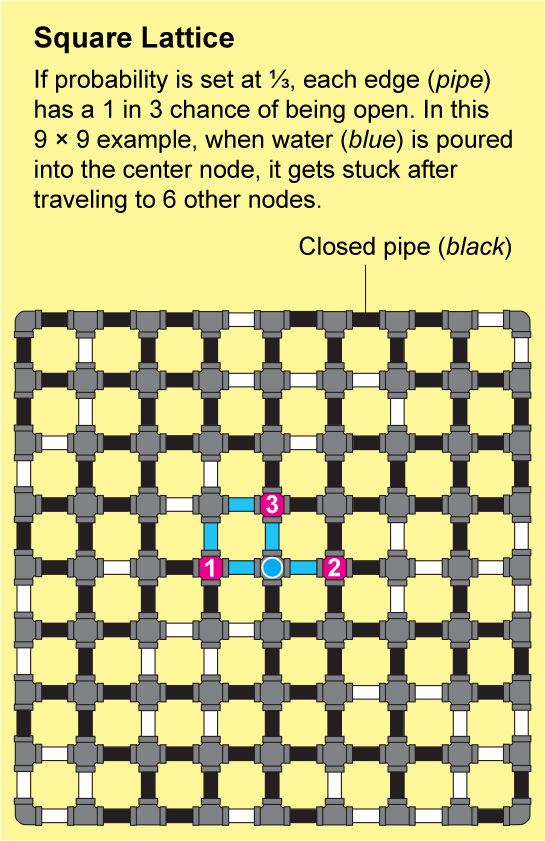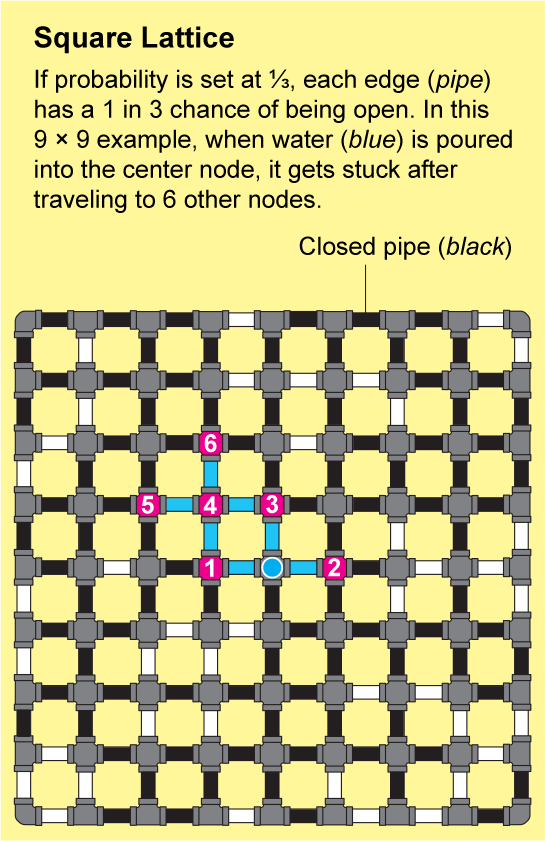
圖片來源:Jen Christiansen
圖片來源:Jen Christiansen
滲流理論關注網路的連通性,這對應於開啟的簇有多大。“大”是一個模糊的概念,不容易進行數學形式化。因此,數學家經常用無窮大代替大數。因此,中心問題變成了:是否存在無限簇?“對我們來說,回答這個是或否的問題比回答我們看到了多少個這種或那種大小的大簇要容易得多,”柏林魏爾斯特拉斯應用分析與隨機研究所的數學家貝內迪克特·亞內爾說。
事實上,無限網路具有無限簇的可能性總是 0 或 100%。這是因為滲流過程受機率論中的一個普遍原則支配,即零一律,由俄羅斯數學家安德烈·柯爾莫哥洛夫在 20 世紀 30 年代發現。假設你無限次地拋擲一枚硬幣。零一律適用於任何關於結果的問題,其答案不依賴於任何有限次數的拋擲。(例如,對於問題“你拋擲出正面無限多次了嗎?”的答案,如果你改變有限次數的拋擲,答案不會改變,但是對於問題“你在第三次拋擲中拋擲出正面了嗎?”的答案,可以透過僅改變一次拋擲來改變。)
零一律告訴我們,有限的變化不會擾亂無限性質的現象。因此,在無限網路中找到無限簇的機率不能稍微改變,例如從 0.81 變為 0.82;它必須採取極端位置之一——零或一。換句話說,無限網路要麼沒有無限簇(找到無限簇的機率為零),要麼有無限簇(機率為一)。
因此,將有限數量的開啟管道切換為關閉管道,反之亦然,對是否存在無限開啟簇沒有任何影響。找到無限簇的機率要麼是零,要麼是一。是哪個呢?
找到閾值
答案取決於你的硬幣的偏差。想象你有一個控制偏差的撥盤。當撥盤完全向左轉動時,硬幣將始終落在“關閉”面上。一旦所有管道都關閉,倒入節點的水將不會流到任何地方,並且找到無限簇的機率將為零。當你順時針轉動撥盤時,硬幣落在“開啟”面上的機率會增加,並且隨著額外的拋擲,將會有越來越多的開啟管道。當撥盤完全向右轉動時,硬幣將始終落在“開啟”面上,最終倒入一個節點的水將流到其他所有地方。然後,找到無限簇的機率為一。
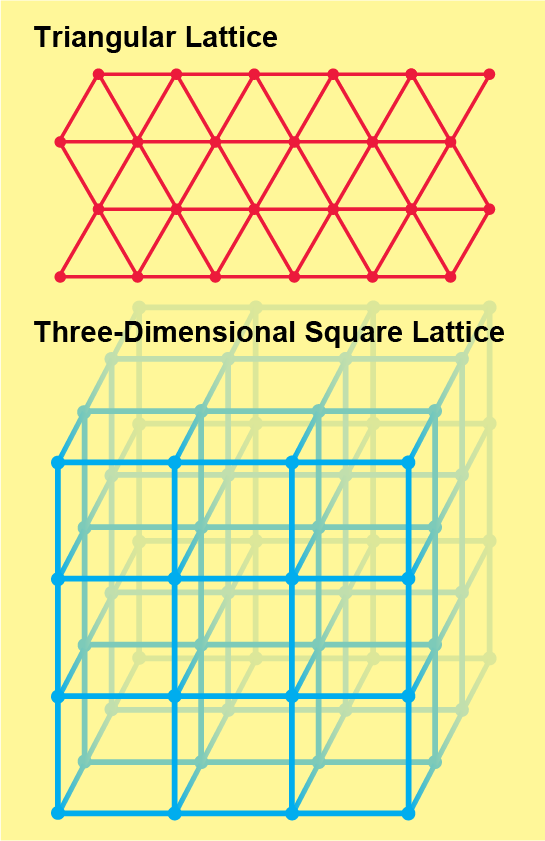
如果你緩慢地順時針轉動撥盤,管道開啟的可能性會逐漸增加,並且似乎找到無限簇的機會也應該從零逐漸增加到一。事實上,由於零一律,變化會瞬間發生:它表明可能性不能介於零和一之間。對於正方晶格,當撥盤正好在中間時——當硬幣沒有偏差時,機率會從零突變為一。撥盤的這個臨界位置被稱為滲流閾值。無論網路的形狀如何——例如,它是三角晶格還是正方晶格的三維版本——滲流理論的本質問題仍然相同:閾值在哪裡?在保證有足夠的連結開啟以保證無限開啟簇之前,硬幣需要有多大的偏差?
圖片來源:Jen Christiansen
答案取決於(無限)網路的精確形狀,並且遠非易於找到。即使證明正方晶格——最簡單的系統——的閾值為二分之一也是一個艱鉅的挑戰,數學家哈里·克斯頓在 1980 年最終解決了這個問題。儘管經過數十年的努力,但精確的滲流閾值僅對少數極其簡單的網路是已知的。“僅僅為了找到閾值就做了大量的工作,”密歇根大學的統計物理學家羅伯特·M·齊夫說。“人們研究了多少不同的系統,真是令人難以置信。”齊夫整理了一個維基百科頁面,記錄了數百個不同網路的滲流閾值。三角晶格的偏差約為 0.347,這個數字是透過分析確定的,但該頁面上的絕大多數數字(包括三維正方晶格的閾值偏差)都是透過計算機模擬得出的近似值。
網狀網路
晶格是物理系統中滲流的良好模型,例如裂縫岩石,其中孔洞的位置是固定的,並且它們之間的裂縫隨機形成。但是,其他現實世界的網路要複雜得多。例如,在前面提到的 FireChat 和 Bridgefy 網狀網路中,節點的位置——香港抗議者攜帶的手機——不斷變化。當兩部手機彼此足夠靠近時——在用於共享訊息的基於藍牙的應用程式的數十米範圍內,網路中的邊或連線就會形成。這種網路由不同的模型描述,稱為連續滲流,因為網狀網路的節點可以位於連續空間中的任何位置。
像任何數學模型一樣,這個網路的抽象版本基於簡化的假設。智慧手機是隨機分散的,沒有模仿人們蜿蜒路線圖中的自然簇和模式,並且兩部智慧手機僅根據它們之間的距離連線,而沒有考慮牆壁或其他干擾。儘管如此,該模型仍然突出了滲流理論在真實網狀網路中發揮的核心作用。
有兩種方法可以提高這種連續滲流網路的連通性:啟用更長範圍的直接連線或新增更多智慧手機,從而增加使用者密度。這些修改可以被認為是像管道網路中描述的那些撥盤;順時針轉動任何一個撥盤都會增加連通性。並且在這些模型中,“存在一個開關,你真的可以從區域性連通性轉變為全域性連通性,”亞內爾說。
對於網狀網路應用程式的設計者來說,找到滲流閾值是一個實際的工程問題。更改裝置的功率(控制範圍)是轉動撥盤的一種方式。網狀網路公司 goTenna 的首席科學家拉姆·拉馬納坦說,中心問題是,“你希望發射功率是多少才能擁有一個連線的網路?”如果功率和連通性具有線性關係——如果功率的每次小幅增加都導致連通性的成比例小幅增加,那麼答案將非常簡單。但是滲流閾值的存在意味著存在網路會隨著人們的移動而突然失去連通性的風險。最佳功率是既能確保網路始終連線又不會浪費能量的功率。
另一個撥盤是手機的密度。具有固定範圍的網狀網路需要臨界使用者密度,並且最有可能在擁擠的活動(例如音樂節、足球比賽或大型抗議活動)中提供廣泛的連通性。Bridgefy 的執行長兼聯合創始人豪爾赫·里奧斯說,該公司看到在克什米爾、奈及利亞、香港和伊朗的內亂時期,新使用者大幅增加,當時人們轉向網狀網路,以便在政府關閉網際網路或大量人群阻塞蜂窩連線時保持通訊。紐約布魯克林的紅鉤區等一些社群正在使用網狀網路,透過將永久節點固定在建築物頂部來擴充套件網際網路接入。許多必要的硬體和路由技術仍在發展中,但很容易想象大膽的、未來的應用——例如,自動駕駛汽車可以直接通訊,共享關於交通模式或道路危險的資訊,而無需依賴任何額外的基礎設施。
疾病接觸網路
用於模擬石油在岩石中流動或手機之間直接通訊的網路模仿了這些系統的真實空間結構:如果它們代表的物件在物理空間中彼此靠近,則兩個節點透過一條邊連線。但是,對於跟蹤疾病在人與人之間傳播的網路,連結由特定病菌在他們之間傳播的方式決定。這種網路特別複雜:一個受感染的人在大城市的一家夜總會里待了一個小時,可能會將病毒傳播給一個人,這個人會在接下來的幾天裡將病毒帶到全國甚至跨越大陸。
最簡單的流行病學模型將每個人分為三類——易感人群、感染人群和康復人群——並忽略了這種複雜的連線結構。在這樣的模型中,感染者在假設該組中的每個人——宿舍裡的學生或城市居民——同樣容易感染的情況下,將疾病傳播給易感人群中的隨機其他人。易感人群被感染的速度取決於基本再生數,即單個感染者引起的平均新感染數,縮寫為 R0。如果 R0 大於 1,則病毒正在傳播,如果小於 1,則疫情正在消退。
然而,在實踐中,人們彼此之間的互動方式會影響疾病的整體傳播。例如,2003 年爆發的嚴重急性呼吸綜合徵(SARS)最初的 R0 值介於 2.2 和 3.6 之間,但病例數“遠低於此期間的預期,正如一個簡單的計算所表明的那樣,”勞倫·安塞爾·邁耶斯寫道,她現在是德克薩斯大學 COVID-19 建模聯盟的主任,她在2006 年的一篇文章中寫道。她認為,這種差異源於“所有易感個體都同樣容易被感染”的假設,該假設忽略了人們接觸網路的複雜形狀。特別是,SARS 的估計 R0 值是基於其在公寓樓和醫院中的快速傳播,與普通人群相比,這些場所“個體之間的密切接觸率異常高”。但是,由於感染 SARS 的人很快就會病得很重,因此他們在醫院中結束治療,然後才可能感染醫院外面的許多人。
疾病網路中的邊表示特定的關係。例如,在顯示 HIV 潛在傳播的網路中,如果兩個人交換了體液,則他們透過一條邊連線。顯示 COVID-19 潛在傳播的網路具有非常不同的邊結構,表示在沒有呼吸防護的情況下進行密切接觸。封鎖或限制,例如關閉企業和限制旅行,會改變這種邊結構,並與口罩和身體疏遠一起,阻止病毒從一個人或節點傳播到另一個人或節點。流行病學家面臨的一個挑戰是找到充分斷開網路連線的方法。
現實世界中的疾病接觸網路,例如顯示 COVID-19 傳播的網路,極其複雜且難以精確描述。即使網路的精確結構是已知的,在數學上分析它也將具有挑戰性。計算機模擬和海量資料分析被用於預測未來的病例數,評估一米與兩米社交距離的影響,並量化學校和餐館在冠狀病毒傳播中的重要性。東北大學的複雜網路理論家亞歷山德羅·韋斯皮尼亞尼將這項研究稱為他的“戰時”工作——戰術性的,偶爾也很混亂,但產生了決策者和醫護人員需要的直接的數字結果。韋斯皮尼亞尼和他的同事建立了“一種合成社會,其中所有這些個體都被打包到一臺計算機中”以執行模擬,他說。
相比之下,韋斯皮尼亞尼將他的“和平時期”研究稱為“你開發模型,你校準不同的建模事物方式,你開發特定的方法,你研究如何改進你的結果”的時期。為了獲得對網路的基本形狀和結構特徵如何影響疾病傳播的理論理解,科學家們轉向了滲流理論。
傳統的紙筆滲流數學工具僅在最簡單的情況下才有效,在這些情況下,網路是人為有序和對稱的。即便如此,“數學對於指導你的理解至關重要,”韋斯皮尼亞尼說。網路流行病學家將網路簡化為最基本要素,特別是其所謂的度分佈。度是特定節點連線到的其他節點的數量。例如,在正方晶格中,所有節點的度均為 4。然而,在疾病網路中,度數差異很大:有些人有很多接觸,並且可能將疾病傳播給很多人,而另一些人則相當孤立。
度分佈描述了節點具有每個度的可能性。在疾病接觸網路中,這轉化為某人感染(或可能被感染)一定數量的其他人的可能性。為了理解這個方面如何影響滲流閾值,像邁耶斯這樣的數學流行病學家生成了數千個樣本網路,這些網路本質上是隨機的,但只有一個特徵:它們都具有相同的度分佈。這種方法是一種分離度分佈的方式,以感知其在網路結構中的作用。如果生成的網路的屬性與真實世界的網路相匹配,那麼“融入數學的”度分佈或任何其他特徵可能與疾病的傳播相關,邁耶斯說。如果匹配是完美的,“那麼你的數學結果將看起來就像你的模擬。”
研究表明,如果網路具有更廣泛的度分佈,即節點度數的範圍更廣,則網路的滲流閾值會降低。因此,在具有一些高度連線的人和一些孤立個體的網路中,疾病比在每個人都具有大致相同接觸次數的網路中更容易傳播。澳大利亞墨爾本拉籌伯大學的數學流行病學家喬爾·米勒啟發式地解釋了這種觀察:“如果我的接觸次數是你的 10 倍,那麼我被感染的可能性是你的 10 倍,我傳播的可能性也是你的 10 倍,因此這對於疾病傳播的重要性是 100 倍。”
未來的網路
滲流理論被用於模擬其他“傳染”現象,例如社交媒體網路上的模因在突然走紅之前緩慢獲得關注的情況。它可以應用於經濟模型,以展示當人們在社交聯絡人之間分享推薦時,特定產品如何迅速佔據市場主導地位。選民模型(人們影響其社群)也顯示出閾值效應。
與數學家傳統上研究的無限的、整齊有序的網路相反,從真實示例中派生的網路在範圍上是有限的且混亂的。有限網路不會像無限網路那樣立即從在小範圍內連線跳躍到幾乎在所有地方都連線,但它們通常確實會非常快速地進行切換。為了理解這些過程,網路理論家在數學和計算機模擬之間來回切換。更簡單的網路指導他們構建實際網路的詳細計算機模型,從中吸取的教訓反過來又影響了他們如何修改紙筆模型,以深入瞭解現實世界。
COVID-19 傳播的許多重要網路模型都集成了來自其他網路的資訊。學校系統、火車路線和醫院員工時間表都形成了網路——並且每個網路都會影響疫情的程序。“我們生活在這個相互依存的網路系統中,我們不能只考慮一個網路而不瞭解其他網路帶來的後果,”加州大學戴維斯分校的複雜網路理論家拉伊薩·德索薩說。每個網路都是其自身的複雜系統,具有其自身的湧現行為。我們越來越多地將這些網路耦合起來,以建立一個更加複雜的系統。但是,沒有明確的理論框架來研究這種網路網路。理解它們的屬性如何受到組成網路的屬性的影響是未來的一個挑戰。
“我們不是生活在一個泡沫中或一個完全混合的世界中。我們生活在一個有聯絡的世界中,我們關注 Twitter 帳戶,而這些是滲流和其他模型進入的地方,”韋斯皮尼亞尼說。現在更好地理解這些理論數學模型“可以在未來發揮作用”。滲流網路易於適應,為數學家提供了新的遊樂場,為科學家提供了實際應用,但這些多樣化的模型由一個令人驚訝的特徵統一起來:它們都具有一個急劇的支點,只需幾個新的連線就可以將網路連線在一起。隨著世界變得越來越互聯,理解這些關鍵轉變的必要性變得越來越迫切。

