我們都曾有過因試圖設定密碼,卻被告知密碼太弱而感到沮喪的經歷。我們也經常被告知要定期更改密碼。顯然,這些措施增加了安全性,但究竟是如何增加的呢?
我將解釋一些標準建議背後的數學原理,包括闡明為什麼六個字元不足以構成一個好的密碼,以及為什麼您永遠不應該只使用小寫字母。我還將解釋駭客如何在被盜資料集中即使沒有密碼也能破解密碼。
明智地選擇密碼#W!sely@*
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您將幫助確保未來能夠繼續釋出關於塑造當今世界的發現和思想的具有影響力的報道。
以下是設定防駭客密碼背後的邏輯。當您被要求建立一個具有特定長度和元素組合的密碼時,您的選擇將符合符合該規則的所有唯一選項的範圍——即“可能性空間”。例如,如果您被告知使用六個小寫字母——例如,afzjxd、auntie、secret、wwwwww——則空間將包含 266,即 308,915,776 種可能性。換句話說,第一個字母有 26 種可能的選擇,第二個字母有 26 種可能的選擇,依此類推。這些選擇是獨立的:您不必使用不同的字母,因此密碼空間的大小是可能性的乘積,即 26 x 26 x 26 x 26 x 26 x 26 = 266。
如果您被告知選擇一個 12 個字元的密碼,該密碼可以包含大寫和小寫字母、10 個數字和 10 個符號(例如,!、@、#、$、%、^、&、?、/ 和 +),則密碼的 12 個字元中的每一個字元將有 72 種可能性。可能性空間的大小將為 7212 (19,408,409,961,765,342,806,016,或接近 19 x 1021)。
這比第一個空間大 62 萬億倍以上。一臺計算機逐個遍歷您的 12 個字元密碼的所有可能性,將花費 62 萬億倍的時間。如果您的計算機花費一秒鐘訪問六個字元的空間,那麼它將不得不花費兩百萬年的時間來檢查 12 個字元空間中的每個密碼。大量的可能性使得駭客難以實施對於六個字元空間來說可能可行的攻擊計劃。
透過計算機計算這些空間的大小通常涉及計算可能性數量中的二進位制位數。該數字 N 來自以下公式:1 + integer(log2(N))。在該公式中,log2(N) 的值是一個帶有許多小數位的實數,例如 log2(266) = 28.202638…。公式中的“integer”表示省略該對數值的小數部分,向下舍入為整數——如 integer(28.202638… 28)。對於上面六個小寫字母的示例,計算結果為 29 位;對於更復雜的 12 個字元的示例,計算結果為 75 位。(數學家將可能性空間分別稱為具有 29 位和 75 位的熵。)法國國家網路安全機構 (ANSSI) 建議,當涉及到密碼或絕對必須安全的加密系統的金鑰時,空間應至少具有 100 位。加密涉及以一種方式表示資料,以確保除非接收者擁有秘密的破譯金鑰,否則無法檢索資料。事實上,該機構建議可能性空間為 128 位,以保證未來幾年的安全性。它認為 64 位非常小(非常弱);64 到 80 位小;80 到 100 位中等(中等強度)。
摩爾定律(該定律指出,在一定價格下可用的計算機處理能力大約每兩年翻一番)解釋了為什麼相對較弱的密碼不足以長期使用:隨著時間的推移,使用蠻力的計算機可以更快地找到密碼。儘管摩爾定律的速度似乎正在下降,但對於您希望長期保持安全的密碼,明智的做法是將其考慮在內。
對於 ANSSI 定義的真正強大的密碼,您將需要,例如,一個由 16 個字元組成的序列,每個字元取自一組 200 個字元。這將構成一個 123 位的空間,這將使密碼幾乎不可能記住。因此,系統設計人員通常要求較低,並接受低強度或中等強度的密碼。只有當密碼由系統自動生成,且使用者不必記住密碼時,他們才會堅持使用長密碼。
還有其他方法可以防止密碼破解。最簡單的方法是信用卡常用的眾所周知的方法:在三次嘗試失敗後,訪問將被阻止。還提出了其他替代想法,例如在每次連續嘗試失敗後將等待時間加倍,但允許系統在一段較長時間(例如 24 小時)後重置。然而,當攻擊者能夠在未被檢測到的情況下訪問系統,或者如果系統無法配置為中斷和停用失敗的嘗試時,這些方法是無效的。
.jpg?w=900)
搜尋所有可能的密碼需要多長時間?
為了使密碼難以破解,應從大量的可能性集合或“空間”中隨機選擇密碼。可能性空間的大小 T 取決於密碼中有效字元列表的長度 A 和密碼中的字元數 N。這個空間的大小 (T = AN) 可能差異很大。
以下每個示例都指定了 A、N、T 的值以及駭客必須花費的時間 D(小時),才能逐個嘗試每個字元排列。 X 是在假設摩爾定律(計算能力每兩年翻一番)仍然有效的情況下,空間可以在不到一小時內檢查完畢之前必須經過的年數。我還假設在 2019 年,一臺計算機每秒可以探索十億種可能性。我用以下三個關係式表示這組假設,並考慮基於 A 和 N: 值的五種可能性
關係式
T = AN
D = T/(109 × 3,600)
X = 2 log2[T/(109 × 3,600)]
結果
_________________________________
如果 A = 26 且 N = 6,則 T = 308,915,776
D = 0.0000858 計算小時
X = 0;已經可以在一小時內破解該空間中的所有密碼
_________________________________
如果 A = 26 且 N = 12,則 T = 9.5 × 1016
D = 26,508 計算小時
X = 29 年後密碼可以在一小時內被破解
_________________________________
如果 A = 100 且 N = 10,則 T = 1020
D = 27,777,777 計算小時
X = 49 年後密碼可以在一小時內被破解
_________________________________
如果 A = 100 且 N = 15,則 T = 1030
D = 2.7 × 1017 計算小時
X = 115 年後密碼可以在一小時內被破解
________________________________
如果 A = 200 且 N = 20,則 T = 1.05 × 1046
D = 2.7 × 1033 計算小時
X = 222 年後密碼可以在一小時內被破解
武器化字典和其他駭客技巧
攻擊者通常會成功從系統中獲取加密密碼或密碼“指紋”(稍後我將更全面地討論)。如果駭客攻擊未被檢測到,入侵者可能有幾天甚至幾周的時間來嘗試推匯出實際密碼。
為了理解在這種情況下利用的微妙過程,請再次審視可能性空間。當我之前談到位大小和密碼空間(或熵)時,我隱含地假設使用者始終隨機選擇密碼。但通常選擇不是隨機的:人們傾向於選擇他們可以記住的密碼(locomotive),而不是任意的字元字串(xdichqewax)。
這種做法對安全性構成嚴重問題,因為它使密碼容易受到所謂的字典攻擊。常用的密碼列表已被收集並根據其使用頻率進行分類。攻擊者透過系統地瀏覽這些列表來嘗試破解密碼。這種方法非常有效,因為在沒有具體約束的情況下,人們自然會選擇簡單的單詞、姓氏、名字和簡短的句子,這大大限制了可能性。換句話說,密碼的非隨機選擇本質上縮小了可能性空間,從而減少了解開密碼所需的平均嘗試次數。
以下是其中一個密碼字典中的前 25 個條目,按順序列出,從最常見的密碼開始。(我從 2017 年洩露並由 SplashData 分析的 500 萬個密碼的資料庫中提取了示例。)
1. 123456
2. password
3. 12345678
4. qwerty
5. 12345
6. 123456789
7. letmein
8. 1234567
9. football
10. iloveyou
11. admin
12. welcome
13. monkey
14. login
15. abc123
16. starwars
17. 123123
18. dragon
19. passw0rd
20. master
21. hello
22. freedom
23. whatever
24. qazwsx
25. trustno1
如果您使用 password 或 iloveyou,您並沒有您想象的那麼聰明!當然,列表會因收集列表的國家和所涉及的網站而異;它們也會隨著時間而變化。
對於四位數字密碼(例如,智慧手機上 SIM 卡的 PIN 碼),結果更缺乏想象力。2013 年,根據 DataGenetics 網站收集的 340 萬個每個包含四位數字的密碼,最常用的四位數字序列(佔選擇的 11%)是 1234,其次是 1111(6%)和 0000(2%)。最少使用的四位數字密碼是 8068。不過,請注意,由於結果已釋出,此排名可能不再真實。在資料庫中的 340 萬個四位數字序列中,8068 這個選擇僅出現 25 次,遠低於如果每個四位數字組合的使用頻率相同,則應出現的 340 次使用。前 20 個四位數字系列是:1234;1111;0000;1212;7777;1004;2000;4444;2222;6969;9999;3333;5555;6666;1122;1313;8888;4321;2001;1010。
即使沒有密碼字典,使用語言中字母使用頻率(或雙字母)的差異也可以計劃有效的攻擊。一些攻擊方法還考慮到,為了方便記憶,人們可能會選擇具有特定結構的密碼——例如 A1=B2=C3、AwX2AwX2 或 O0o.lli.(我長期使用)——或者透過組合幾個簡單的字串來派生密碼,例如 password123 或 johnABC0000。利用這些規律性可以使駭客加快檢測速度。
雜湊駭客
正如正文解釋的那樣,網際網路伺服器不儲存客戶端的密碼,而是儲存這些密碼的“指紋”:從密碼派生的字元序列。在發生攻擊時,使用指紋可以使駭客很難(如果不是不可能)使用他們發現的內容。
這種轉換是透過使用稱為加密雜湊函式的演算法來實現的。這些是精心開發的過程,可以將資料檔案 F(無論其長度如何)轉換為序列 h(F),稱為 F 的指紋。例如,雜湊函式 SHA256 將短語“Nice weather”轉換為
DB0436DB78280F3B45C2E09654522197D59EC98E7E64AEB967A2A19EF7C394A3
(64 個十六進位制或 16 進位制字元,相當於 256 位)
更改檔案中的單個字元會完全改變其指紋。例如,如果 Nice weather 的第一個字元更改為小寫 (nice weather),則雜湊 SHA256 將生成另一個指紋
02C532E7418CD1B57961A1B090DB6EC37B3C58380AC0E6877F3B6155C974647E
您可以自己進行這些計算並在 https://passwordsgenerator.net/sha256-hash-generator 或 www.xorbin.com/tools/sha256-hash-calculator 上檢視它們
良好的雜湊函式生成的指紋類似於如果均勻隨機選擇指紋序列所獲得的指紋。特別是,對於任何可能的隨機結果(64 個十六進位制字元的序列),在合理的時間內不可能找到具有此指紋的資料檔案 F。
雜湊函式已經經歷了幾個發展階段。SHA0 和 SHA1 世代已經過時,不建議使用。包括 SHA256 在內的 SHA2 世代被認為是安全的。
給消費者的啟示
考慮到所有這些,設計良好的網站會在建立密碼時分析使用者提出的密碼,並拒絕那些太容易恢復的密碼。這很煩人,但為了您好。
對於使用者來說,顯而易見的結論是他們必須隨機選擇密碼。一些軟體確實提供了隨機密碼。但是,請注意,此類密碼生成軟體可能有意或無意地使用不良的偽隨機生成器,在這種情況下,它提供的密碼可能並不完美。
您可以使用名為 Pwned Passwords (https://haveibeenpwned.com/Passwords) 的 Web 工具檢查您的任何密碼是否已被駭客入侵。其資料庫包含超過 5 億個在各種攻擊後獲得的密碼。
我嘗試了 e=mc2e=mc2,我喜歡這個密碼並認為它很安全,但收到了令人不安的回覆:“此密碼之前已被看到 114 次。” 其他嘗試表明,很難想出資料庫不知道的易於記憶的密碼。例如,aaaaaa 出現了 395,299 次;a1b2c3d4 出現了 113,550 次;abcdcba 出現了 378 次;abczyx 出現了 186 次;acegi 出現了 117 次;clinton 出現了 18,869 次;bush 出現了 3,291 次;obama 出現了 2,391 次;trump 出現了 859 次。
仍然有可能保持原創性。例如,該網站無法識別以下六個密碼:eyahaled(我的名字倒過來拼寫);bizzzzard;meaudepace 和 modeuxpass(法語“密碼”的兩個雙關語);abcdef2019;passwaurde。既然我已經嘗試過它們,我想知道資料庫下次更新時是否會新增它們。如果是這樣,我就不會使用它們了。
給網站的建議
網站也遵循各種經驗法則。美國國家標準與技術研究院最近釋出了一份通知,建議使用字典來過濾使用者的密碼選擇。
優秀的 Web 伺服器設計人員絕對必須遵守的規則之一是,不要將使用者名稱和密碼的明文列表儲存在用於執行網站的計算機上。
原因很明顯:駭客可能會訪問包含此列表的計算機,原因可能是該站點保護不力,或者系統或處理器包含除攻擊者外無人知曉的嚴重缺陷(所謂的零日漏洞),攻擊者可以利用該漏洞。
一種替代方法是在伺服器上加密密碼:使用秘密程式碼,透過加密金鑰將密碼轉換為對於任何沒有解密金鑰的人來說都像是隨機字元序列的內容。這種方法有效,但有兩個缺點。首先,每次將其與使用者條目進行比較時,都需要解密儲存的密碼,這很不方便。其次,更嚴重的是,這種比較所需的解密需要在網站計算機的記憶體中儲存解密金鑰。因此,攻擊者可能會檢測到此金鑰,這使我們回到了最初的問題。
儲存密碼的更好方法是透過稱為雜湊函式的方法,該方法生成“指紋”。對於檔案中的任何資料(符號化為 F),雜湊函式都會生成指紋。(該過程也稱為壓縮或雜湊。)指紋 h(F) 是與 F 關聯的相當短的單詞,但以一種方式生成,實際上,不可能從 h(F) 推匯出 F。雜湊函式被稱為單向的:從 F 到 h(F) 很容易;從 h(F) 到 F 實際上是不可能的。此外,使用的雜湊函式具有以下特性:即使兩個資料輸入 F 和 F' 可能具有相同的指紋(稱為衝突),但在實踐中,對於給定的 F,幾乎不可能找到指紋與 F 相同的 F'。
使用此類雜湊函式可以將密碼安全地儲存在計算機上。伺服器不儲存配對的使用者名稱和密碼列表,而是僅儲存使用者名稱/指紋對列表。
當用戶希望連線時,伺服器將讀取個人的密碼,計算指紋,並確定它是否與與該使用者名稱關聯的儲存使用者名稱/指紋對列表相對應。這種操作挫敗了駭客,因為即使他們設法訪問了列表,他們也無法推匯出使用者的密碼,因為實際上不可能從指紋轉到密碼。他們也無法生成另一個具有相同指紋的密碼來愚弄伺服器,因為實際上不可能建立衝突。
儘管如此,沒有一種方法是萬無一失的,主要網站頻繁遭到駭客攻擊的報告就突顯了這一點。例如,2016 年,雅虎!有 10 億個帳戶的資料被盜!
為了增加安全性,有時會使用一種稱為加鹽的方法來進一步阻止駭客利用被盜的使用者名稱/指紋對列表。加鹽是在每個密碼中新增唯一的隨機字元字串。它確保即使兩個使用者使用相同的密碼,儲存的指紋也會不同。伺服器上的列表將包含每個使用者的三個組成部分:使用者名稱、在密碼中新增鹽後派生的指紋以及鹽本身。當伺服器檢查使用者輸入的密碼時,它會新增鹽,計算指紋,並將結果與其資料庫進行比較。
即使在使用者密碼較弱的情況下,此方法也大大增加了駭客的工作難度。在不加鹽的情況下,駭客可以計算字典中的所有指紋,並檢視被盜資料中的指紋;可以識別駭客字典中的所有密碼。透過加鹽,對於使用的每種鹽,駭客都必須計算駭客字典中所有密碼的加鹽指紋。對於一組 1,000 個使用者,這將使使用駭客字典所需的計算量增加 1,000 倍。
適者生存
毋庸置疑,駭客有自己的反擊方式。但他們面臨著一個困境:他們最簡單的選擇要麼需要大量的計算能力,要麼需要大量的記憶體。通常這兩種選擇都不可行。但是,有一種稱為彩虹表方法的折衷方法(請參閱“彩虹表幫助駭客”)。
在網際網路、超級計算機和計算機網路的時代,密碼設定和破解的科學不斷發展——保護密碼的人和決心竊取和可能濫用密碼的人之間的無情鬥爭也在不斷發展。
彩虹表幫助駭客
假設您是一名駭客,希望利用您已獲得的資料。這些資料由使用者名稱/指紋對組成,並且您知道雜湊函式(請參閱“雜湊駭客”)。密碼包含在 12 個小寫字母字串的可能性空間中,這對應於 56 位資訊和 2612 (9.54 x 1016) 個可能的密碼。
至少有兩種強大的方法可供您選擇
方法 1。您滾動瀏覽整個密碼空間。您計算每個密碼的指紋 h(P),檢查它是否出現在被盜資料中。您不需要大量記憶體,因為之前的結果會在每次新嘗試時被刪除,儘管您當然必須跟蹤已測試的可能性。
以這種方式滾動瀏覽所有可能的密碼需要很長時間。如果您的計算機每秒執行十億次測試,您將需要 2612/(109 x 3,600 x 24) 天(1,104 天),或大約三年才能完成此任務。這個壯舉並非不可能;如果您碰巧擁有一個由 1,000 臺機器組成的計算機網路,一天就足夠了。但是,每次您希望測試其他資料時(例如,如果您獲得一組新的使用者名稱/指紋對),重複此類計算是不可行的。(因為您沒有儲存計算結果,所以您將需要額外的 1,104 天來處理新資訊。)
方法 2。您對自己說,“我將計算所有可能的密碼的指紋,這將需要時間,並且我將把生成的指紋儲存在一個大表中。然後,我只需在表中找到一個密碼指紋即可識別被盜資料中的相應密碼。”
您將需要 (9.54 x 1016) x (12 + 32) 位元組的記憶體,因為該任務需要 12 位元組用於密碼,如果指紋包含 256 位(假設 SHA256 函式),則需要 32 位元組用於指紋。那是 4.2 x 1018 位元組,或 420 萬個容量為 1TB 的硬碟驅動器。
此記憶體需求太大。方法 2 與方法 1 一樣不可行。方法 1 需要太多的計算,而方法 2 需要太多的記憶體。這兩種情況都很成問題:要麼每個新密碼都需要很長時間才能計算出來,要麼預先計算所有可能性並存儲所有結果的任務太大。
是否有某種折衷方案,既比方法 1 需要更少的計算能力,又比方法 2 需要更少的記憶體?確實有。1980 年,斯坦福大學的馬丁·赫爾曼提出了一種方法,該方法在 2003 年由瑞士洛桑聯邦理工學院的菲利普·厄克斯林改進,並在最近由法國雷恩國立應用科學學院 (INSA Rennes) 的吉爾達斯·阿沃因進一步改進。它需要比方法 1 更少的計算能力,以換取使用稍多的記憶體。
彩虹之美
以下是它的工作原理:首先,我們需要一個函式 R,將指紋 h(P) 轉換為新密碼 R(h(P))。例如,人們可以將指紋視為以二進位制數字系統編寫的數字,並將密碼視為以 K 進位制數字系統編寫的數字,其中 K 是密碼允許的符號數。然後,函式 R 將資料從二進位制數字系統轉換為 K 進位制數字系統。對於每個指紋 h(P),它都會計算一個新的密碼 R(h(P))。
現在,使用此函式 R, 我們可以預先計算稱為彩虹表的資料表(之所以這樣命名,可能是因為這些表以彩色方式描繪)。
為了在此表中生成資料點,我們從可能的密碼 P0 開始,計算其指紋 h(P0),然後計算新的可能密碼 R(h(P0)),即 P1。接下來,我們從 P1 繼續此過程。除了 P0 之外不儲存任何內容,我們計算序列 P1、P2、…直到指紋以 20 個零開頭;該指紋被指定為 h(Pn)。這種指紋大約在 1,000,000 個指紋中出現一次,因為雜湊函式的結果類似於均勻隨機抽取的結果,而 220 大約等於 1,000,000。然後將包含以 20 個零開頭的指紋的密碼/指紋對 [P0, h(Pn)] 儲存在表中。
計算了非常大量的此類對。每個密碼/指紋對 [P0, h(Pn)] 代表密碼序列 P0、P1、… Pn 及其指紋,但該表不儲存那些中間計算。因此,該表列出了許多密碼/指紋對,並代表了更多(中間值,例如可以從列出的對派生的 P1 和 P2)。但是,當然,可能存在差距:某些密碼可能在所有計算鏈中都不存在。
對於幾乎沒有差距的良好資料庫,儲存計算對所需的記憶體比前面描述的方法 2 所需的記憶體小一百萬倍。那不到四個 1TB 的硬碟驅動器。很簡單。此外,正如將要看到的,使用該表從被盜指紋中派生密碼是完全可行的。
讓我們看看硬碟驅動器上儲存的資料如何使您能夠在幾秒鐘內確定給定空間中的密碼。假設沒有差距;表的預計算考慮了指定型別的所有密碼——例如,從 26 個字母的字母表中提取的 12 個字元密碼。
被盜資料集中的指紋 f0 可以透過以下方式用於揭示關聯的密碼。計算 h(R(f0)) 以得到新的指紋 f1,,然後計算 h(R(f1)) 以得到 f2,依此類推,直到您得到一個以 20 個零開頭的指紋:fm。然後檢查表以檢視指紋 fm 與哪個原始密碼 P0 關聯。基於 P0,計算密碼和指紋 h1、h2、…,直到您不可避免地生成原始指紋 f0,指定為 hk。您正在查詢的密碼是產生 hk 的密碼——換句話說,是 R(hk – 1),即計算鏈中早一步的密碼。
所需的計算時間是查詢表中的 fm 所需的時間,加上從關聯密碼計算指紋序列(h1、h2、…、hk)所需的時間——這大約比計算表本身所需的時間短一百萬倍。換句話說,所需的時間非常合理。
因此,透過進行(非常長的)預計算並僅儲存部分結果,可以在合理的時間內檢索具有已知指紋的任何密碼。
以下序列表示從密碼 (Mo, No, ..., Qo) 到指紋和其他密碼的單獨計算鏈,直到所需的指紋(以及因此在其之前的密碼)彈出。 (長虛線表示可能與頂部兩行相似的許多其他行。)
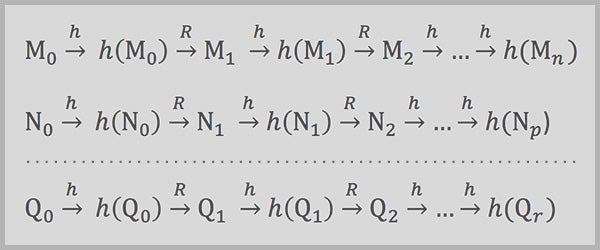
總而言之,透過知道每個計算鏈的開始和結束(預計算期間儲存的唯一內容),駭客可以從指紋中檢索任何密碼。 在某種程度上簡化的術語中,從被盜的指紋(稱之為指紋 X)開始,駭客將重複應用 R 和 h 函式,計算一系列密碼和指紋,直到達到前面有 20 個零的指紋。然後,駭客將在表中查詢最終指紋(以下示例中的指紋 C)並識別其對應的密碼(密碼 C)。
示例表摘錄密碼 A—指紋 A
密碼 B—指紋 B
密碼 C—指紋 C
密碼 D—指紋 D
接下來,駭客將再次應用 h 和 R 函式,從已識別的密碼開始,繼續操作,直到鏈中的一個生成的指紋與被盜的指紋匹配
示例計算密碼 C → 指紋 1 → 密碼 2-- → 指紋 2 → 密碼 3…. → 密碼 22-- →指紋 23 [與指紋 X 匹配!]
匹配項(指紋 23)將表明,從中派生指紋的前一個密碼(密碼 22)是連結到被盜指紋的密碼。
必須進行許多計算才能建立彩虹表的首列和末列。透過僅儲存這兩列中的資料並透過重新計算鏈,駭客可以從其指紋中識別任何密碼。

