喬納森·馬丁利向後靠在椅子上,將雙腿抬到桌子上,按下筆記型電腦上的一個鍵,改變了 2012 年北卡羅來納州的選舉結果。在螢幕上,閃爍的線條和點描繪出該州 13 個國會選區的地圖,每個選區選出一人送往美國眾議院。透過調整這些選區的邊界,但在不改變任何一張選票的情況下,馬丁利的地圖顯示,民主黨的候選人在競選中贏得了六個、七個甚至八個席位。但實際上,他們只贏得了四個席位——儘管贏得了多數選票。
馬丁利的選舉模擬無法改寫歷史,但他希望這些模擬能在未來幫助支援民主——在他的州和整個國家。這位杜克大學(位於北卡羅來納州達勒姆)的數學家設計了一種演算法,可以隨機生成該州選區地圖的替代版本——到目前為止,他已經建立了 24,000 多個版本——作為量化傑利蠑螈現象的程度和影響的嘗試的一部分:當選區被劃分為有利於或不利於某些候選人或政黨時。
傑利蠑螈現象在美國有著悠久而不受歡迎的歷史。這是該國在 2017 年選舉公正性指數中在 158 個國家中排名第 55 位(在西方民主國家中墊底)的主要原因。該指數由選舉誠信專案(澳大利亞悉尼大學和美國馬薩諸塞州劍橋市哈佛大學約翰·F·肯尼迪政府學院之間的學術合作專案)執行。儘管傑利蠑螈現象在動盪的 2016 年總統大選中沒有發揮作用,但它似乎影響了當年誰在美國眾議院贏得了席位。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們今天世界的發現和思想的具有影響力的故事的未來。
馬丁利說:“即使傑利蠑螈現象隻影響了 435 個席位中的 5 個,這也通常足以左右關鍵投票。”
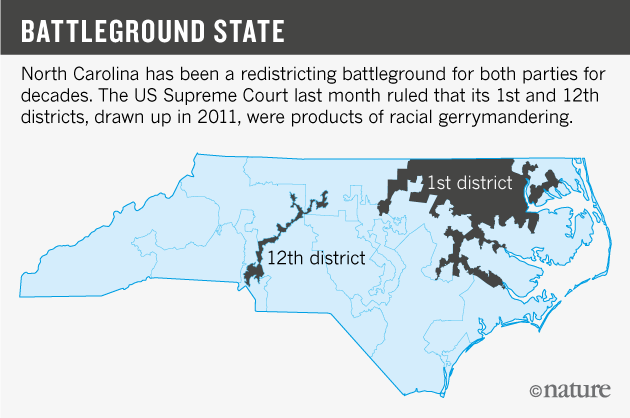
當傑利蠑螈現象是由種族驅動時,法院會進行干預。例如,上個月,最高法院維持了一項判決,即北卡羅來納州的兩個選區在劃定時考慮了種族構成(參見“戰場州”)。但是,法院一直不太願意權衡黨派傑利蠑螈現象——即一個政黨比另一個政黨更受青睞。原因之一是,一直沒有明確且可靠的衡量標準來確定這種型別的傑利蠑螈現象何時從可接受的政治手段越界到違反美國憲法。
馬丁利和其他幾位數學家希望改變這種狀況。在過去的五年中,他們構建了演算法和計算機模型,揭示了選區邊界中的偏差。他們開始被聽到。
2016 年 12 月,威斯康星州一家法院在裁決反對黨派傑利蠑螈現象時,考慮了一項統計分析。馬丁利將在今年夏天在北卡羅來納州的一個案件中擔任專家證人。
儘管此類鬥爭已開始在其他國家(如英國和澳大利亞)出現,但在美國,利害關係尤其高。全國各地正在進行反對黨派傑利蠑螈現象的訴訟,預計 2020 年的人口普查將引發全國範圍內的選區重劃。如果數學家們成功地闡述了他們的觀點,它可能會影響這些地圖的繪製方式。
華盛頓特區律師民權委員會的社會科學家梅根·加爾說:“這就是法院一直在等待的東西。” “這是我們阻止它的方法,”她說。
劃線
1812 年,馬薩諸塞州州長埃爾布里奇·格里簽署了一項法案,該法案重新劃分了一些選區以使其政黨受益。一個形狀怪異的選區環繞波士頓市,形狀像一條蠑螈。政治諷刺作家將新選區戲稱為“格里-蠑螈”。從那時起,這種策略已成為美國政治的主要手段,州立法者以曲折的創造力重新劃分選區。傑利蠑螈現象的兩種主要方法通常被稱為集中和分散。在集中方法中,繪製地圖的政黨的立法者試圖將可能的反對派選民儘可能多地集中到儘可能少的政治選區中。分散方法將競爭對手政黨的支持者分散到幾個選區,降低他們選舉代表的能力,並確保執政黨的勝利(參見“集中和分散”)。

最高法院歷來沒有進行干預,只要選區符合四個標準:它們是連續的;它們是緊湊的;它們包含大致相同數量的人口;並且它們根據 1965 年的《投票權法案》給予少數族裔群體選舉自己代表的機會。在 1986 年的戴維斯訴班德默案中,法院同意它有權干預黨派傑利蠑螈現象案件,但它拒絕這樣做,因為它缺乏明確的衡量標準來表明這種情況何時發生。
作為統計學和機率論專家,馬丁利從未對這個問題進行過太多專業的思考。但他對政治程序的普遍興趣促使他參加了 2013 年的一次公開會議,他在會上聽到一位演講者抨擊北卡羅來納州 2012 年的選舉結果。大約十年來,該州的 13 個選區一直保持相對均勻的劃分。有時民主黨獲得六個席位,有時獲得七個席位。但共和黨在 2012 年選舉前重新劃分選區,將民主黨人集中到三個選區,使該黨處於嚴重劣勢。儘管其候選人贏得了 50.3% 的選票,但該黨只獲得了四個席位。
馬丁利對這種咆哮的熱情和它提出的難題都感到震驚。“如果它真的是不公平的,應該有一種方法可以透過數學來證明這一點,”他說。“我想超越‘他說,她說’,創造更客觀的東西。” 在閱讀有關該問題的資料後,他意識到他有機會建立法官一直在尋找的衡量標準。
集中和分散導致了一些明顯的干預跡象:反對黨往往在集中選區中以壓倒性優勢獲勝,但在分散選區中以微弱優勢失敗。傑利蠑螈現象嚴重的選區更可能在地理上分散且形狀不尋常。馬丁利與一位學生克里斯蒂·格雷夫斯一起開始工作,將這些衡量標準合併為一個單一的、定量的北卡羅來納州傑利蠑螈現象指數。
兩人從該州 2012 年的選區和按街區劃分投票的公共資料開始。然後,他們對選區邊界進行了數千次微小的調整,基本上測試了每個符合最高法院四個標準的迭代。
確保連續性——以及每個選區的人口規模差異僅為 0.1%——相對簡單。保證地圖包含代表數量的非裔美國人和西班牙裔佔多數的選區以符合《投票權法案》也很簡單。
但評估緊湊性是一個挑戰。一個問題是,很難用數學方法分析一個選區是否符合“緊湊”這一相當模糊的書面標準。另一方面,數學家有 30 多種不同的方法來計算形狀的緊湊性,每種方法都會給出略有不同的結果。對於選區來說,哪種方法最好,目前還沒有共識。位於馬薩諸塞州梅德福的塔夫茨大學的數學家穆恩·杜欽在過去幾年中一直在嘗試設計一種用於傑利蠑螈現象的緊湊性指標。“但這個領域一團糟,”她說。
更復雜的是,許多選區由於河流和其他自然邊界而形狀奇特。馬丁利和格雷夫斯開發了一種緊湊性評分,該評分計算為選區周長平方除以其面積,這是所謂的波爾斯比-波普爾度量的一種變體(參見“緊湊劃分”)。圓形具有最低的周長與面積之比;但是,隨著邊界蜿蜒以包含和排除特定區域,周長會擴大,從而給出更高的比率。

憑藉數千張地圖及其產生的投票結果,馬丁利和格雷夫斯可以開始分析北卡羅來納州選區的傑利蠑螈現象有多嚴重。2012 年選舉的 13 個選區中有 3 個民主黨人佔比超過四分之三,比該團隊隨機繪製的任何地圖都更集中,即使對於他們最藍的民主黨選區也是如此。然而,更具說服力的是對選舉結果的影響。使用隨機繪製的地圖,平均有 7.6 個席位歸民主黨所有,而他們實際贏得了 4 個席位(J. Mattingly 和 C. Vaughn 預印本,網址為 http://arxiv.org/abs/1410.8796;2014 年)。“你瞭解得越多,就越令人憤怒,”馬丁利說。
他們對其他州資料的分析揭示了馬里蘭州由民主黨控制的立法機構為排擠其保守派競爭對手而犯下的黨派傑利蠑螈現象。亞利桑那州和愛荷華州等設有獨立或兩黨委員會監督選區建立的州情況要好得多。在另一項分析中,位於賓夕法尼亞州費城的科技公司 Azavea 的地理資訊系統資料分析師丹尼爾·麥格隆 對每個州的選區進行了緊湊性排名,以此作為衡量傑利蠑螈現象的標準,發現馬里蘭州的選區傑利蠑螈現象最嚴重。北卡羅來納州排名第二。內華達州、內布拉斯加州和印第安納州的傑利蠑螈現象最少。
衡量標準
2016 年夏天,一個由退休法官組成的兩黨小組會面,以檢視他們是否可以為北卡羅來納州建立更具代表性的選區。他們的地圖讓馬丁利有機會測試他的指數。他發現,法官們的選區比 75% 的計算機生成模型中的傑利蠑螈現象要輕微——這是一個繪製良好、具有代表性的地圖的標誌。相比之下,在馬丁利、格雷夫斯及其同事在 2017 年 4 月報告的 24,000 個計算機繪製的選區中,每一個都比州立法者繪製的 2012 年或 2016 年的選區傑利蠑螈現象要輕微(S. Bangia et al. 預印本,網址為 http://arxiv.org/abs/1704.03360;2017 年)。
馬丁利說:“我希望這個結果能夠獲得關注。” “它表明選舉結果真的不能代表人民的意願。” 當總部位於華盛頓特區的親民主倡導團體 Common Cause 的代表看到這項工作時,他們邀請馬丁利在今年夏天即將舉行的北卡羅來納州黨派傑利蠑螈現象案件中擔任專家證人。然而,對於研究人員和法官來說,問題是馬丁利的方法是否是最好的。
其他州的數學家也在開發評估傑利蠑螈現象的方法。在伊利諾伊大學厄巴納-香檳分校,政治統計學家溫迪·譚·喬設計了演算法來繪製選區地圖,這些地圖使用州法律規定的標準,但不包括黨派資訊,例如某個地區的投票歷史。透過改變緊湊性評分的重要性,或者每個選區中不同人口的平等程度,她可以生成一組新的選區。喬衡量一個州現有的立法選區與她的超級計算機叢集繪製的數十億張非黨派地圖的吻合程度。喬說,如果它們存在顯著差異,那麼繪製選區的人可能在劃定界線時懷有黨派動機。
喬的方法比馬丁利的方法建立的地圖更多,她說這使其具有優勢。但馬丁利認為,他的演算法更透明,因此可以用來計算法官可能更喜歡的評分。普林斯頓大學神經科學家山姆·王說,這兩種策略都非常技術性,需要專業的專業知識才能實施和解釋。他在業餘時間在普林斯頓選舉聯盟部落格上分析選舉和投票。“最高法院表示,它正在尋找一個‘可管理’的標準。對於憲法問題,法官可能會發現避免必須求助於外部專家更易於管理,”王說。
伊利諾伊大學芝加哥分校的政治學家尼古拉斯·斯特凡諾普洛斯採用了一種更簡單的方法來衡量傑利蠑螈現象。他開發了他所謂的“效率差距”,該差距衡量了一個州的浪費選票:每個選區投給失敗候選人的所有選票,以及超過獲勝所需比例的勝利者的所有選票。如果一個政黨與競爭對手相比,有很多壓倒性的勝利和慘重的失敗,這可能是傑利蠑螈現象的跡象。王說,這種指標的簡單性是一個優勢。
但杜欽認為,僅分析傑利蠑螈現象的一個方面的指標(無論是失衡的勝利還是低緊湊性評分)都不是理想的。她贊成像馬丁利的指標那樣,納入多種促成因素的指標。
然而,佛羅里達大學蓋恩斯維爾分校的政治學家邁克爾·麥克唐納質疑所有這些定量指標的有效性,因為它們依賴於建立所有可能的選區的隨機樣本。他認為,不可能計算出他們正在檢視的樣本的隨機程度。“在美國,繪製選區的方式比宇宙中的夸克還要多。”
英國也出現了對傑利蠑螈現象的指控。英國布里斯托爾大學的地理學家羅恩·約翰斯頓說,直到 20 年前,獨立邊界委員會建立選區的過程在很大程度上是一個非政治過程。約翰斯頓說,在 1990 年代,當時的反對黨工黨的支持者意識到,他們可以透過向邊界委員會提交自己的地圖以供考慮來影響議會選區的建立,這為所有政黨爭奪權力打開了大門。目前正在進行的英國選區改革可能會將議會議員人數減少 50 人;邊界委員會審查的最終結果預計將於 2018 年公佈。預計各政黨將試圖將結果轉向對自己有利的方向,但定量解決方案可能有助於使該過程去政治化。
解決方案在望
加爾說,美國立法者一直不願接受數學方法來解決傑利蠑螈現象。但目前的法庭案件表明,這樣做的壓力越來越大。在威斯康星州惠特福德訴吉爾案中,聯邦法官使用效率差距裁定該州的選區代表著違憲的黨派傑利蠑螈現象。該案件今年晚些時候可能會提交給最高法院。
如果法官要接受傑利蠑螈現象的數學測試,他們將需要馬丁利等專家證人的證詞來解釋這些測試的工作原理和原因。但是,研究該主題的少數數學家不足以應付該國待決的訴訟。即使法院確定了標準指標,法官也可能需要在每個案件中聘請專家。這就是杜欽組織為期一週的夏令營的原因,以幫助數學家瞭解各種傑利蠑螈現象模型的潛在微妙之處,以及如何應用和解釋它們。杜欽預計有 50 人報名;已有 1,000 多人申請。“這個回應讓我們大吃一驚,”她說,現在將舉辦多個夏令營。
馬丁利和他的模型將在今年夏天出庭。即使他的演算法沒有成為標準,馬丁利也希望司法系統能找到一種方法來遏制傑利蠑螈現象,並恢復他對選舉制度的信心。“我也是一名公民,”他說。
本文經許可轉載,並於 首次發表 於 2017 年 6 月 7 日。