在數學史上最離奇的研究實驗之一中,英國普利茅斯大學的研究人員在附近的佩恩頓動物園給六隻蘇拉威西獼猴提供了一臺鍵盤。從2002年5月1日到6月22日,這些動物透過敲擊鍵盤來發洩情緒。它們輸入的字母被傳輸到網際網路上。科學家的目的是檢驗“無限猴子定理”:即猴子在鍵盤上隨機打字,經過無限長的時間後,將產生所有可以想象的文字——包括莎士比亞全集。
但是——驚喜的是——這些靈長類動物的“詩歌”並沒有達到目標。經過七個多星期,獼猴只產生了一份五頁的檔案,幾乎完全由字母“S”組成。儘管如此,研究人員還是將結果作為一本書發表了。
為參與這項實驗的六隻獼猴 Elmo、Gum、Heather、Holly、Mistletoe 和 Rowan 辯護,它們沒有無限的時間來完成這項工作。儘管如此,結果還是令人沮喪的。這些猴子能夠創作出哈姆雷特或“蘇格蘭戲劇”似乎非常值得懷疑。
儘管這項研究絕沒有駁斥無限猴子定理,但它表明,猴子不一定是按照該定理的創立者所假設的方式生成隨機內容的理想候選者。無限猴子定理得名於數學家埃米爾·博雷爾,他在 1913 年用動物作為隱喻來說明他的機率論。然而,該定理背後的思想要古老得多。在古代,羅馬哲學家和政治家馬庫斯·圖留斯·西塞羅寫道,有人可能“相信,如果將大量二十一個字母(由黃金或任何其他物質組成)扔在地上,它們會以清晰可辨的順序排列,形成[史詩]《恩尼烏斯紀年》。[但是]我懷疑命運是否能從中創造出[甚至]一行詩。”
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道: 訂閱。透過購買訂閱,您正在幫助確保未來能夠繼續講述關於發現和塑造我們當今世界的思想的具有影響力的故事。
正如佩恩頓動物園的獼猴所表明的那樣,數學家們已經採取了創造性的步驟來探索這種可能性。今天的研究表明,西塞羅是錯誤的:詩歌可以從這種隨機性練習中產生,前提是你能夠等待很長時間。
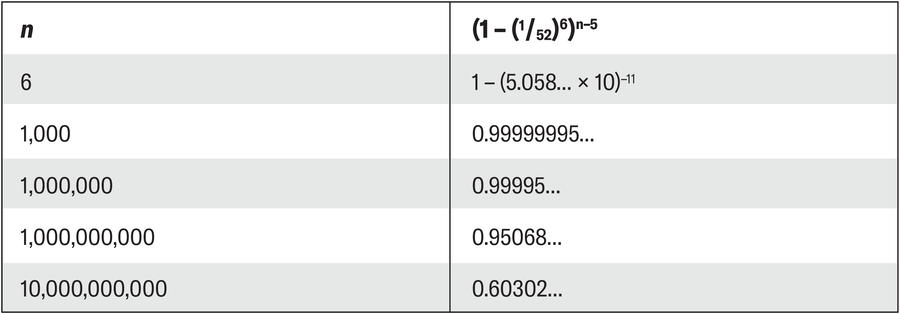
特定單詞出現的機率
讓我們用一個簡單的例子來檢驗這個想法。當你隨機按一系列字母鍵一定次數時,完全偶然地得到單詞“banana”的可能性有多大?(在這種情況下,你不按任何數字或特殊字元。)如果你連續按六個鍵,每個鍵都是隨機選擇的,那麼機率是 (1⁄52)6 = 1⁄19770609664,約為百分之一的五十億分之一。換句話說,不打出 banana 的機率是 1 – (1⁄52)6,這幾乎是 1。總的來說,如果你隨機按六個鍵,那麼得到單詞 banana 的可能性非常小。但是,如果你按鍵的時間更長呢?
如果你隨機按七個鍵的序列,則有兩個連續的六個字母的段可以形成所需的單詞。按八次鍵,則有三個六個字母的字串,依此類推。如果你隨機按鍵盤 n 次,則單詞 banana 不會出現在字串中任何位置的機率為 (1 – (1⁄52)6)n–5。對於 n 值不斷增加的情況,不出現 “banana” 的機率逐漸降低
Manon Bischoff/Spektrum der Wissenschaft,由 Amanda Montañez 重新設計
因此,“banana” 出現的機率逐漸提高:如果你在鍵盤上隨機按鍵 100 億次,那麼該單詞出現在某處的機率突然約為 40%。n 值越大,找到單詞 banana 的機率就越接近於 1。當然,這個結果也適用於其他字母序列、單詞,甚至整個句子和書籍。因此,從數學的角度來看,西塞羅是錯誤的。
實踐中的無限猴子定理
2024 年,巴西聖保羅大學的資料分析師 Ergon Cugler de Moraes Silva 想要 выяснить 平均需要多長時間才能偶然獲得莎士比亞的作品。他沒有使用猴子,而是編寫了一個字元生成器程式。正如在一篇預印本論文中所描述的那樣,他的技術旨在每秒快速生成數百個偽隨機空格、標點符號和字母(包括大寫和小寫),直到出現《哈姆雷特》中的一句名言:“生存還是毀滅,這是一個問題”(包括空格)。
庫格勒分幾個步驟進行。首先,他研究了平均需要多長時間才能單獨找到字母“T”。他重複了該過程 10 次,然後記錄了生成所需輸出所需的平均時間和字元數。然後,他重複此過程以確定隨機生成 “To” 需要多長時間,然後再次對 “To” 後跟一個空格進行同樣的操作,依此類推。
如下表所示,他的程式必須隨機生成約 60 個字元才能產生 “T”,並且平均生成了 345,380,940 個字元才能產生 “To be”。這兩個詞也花費了他的程式大約 1,100 秒(略多於 18 分鐘)。

Manon Bischoff/Spektrum der Wissenschaft,由 Amanda Montañez 重新設計
此時,庫格勒遇到了瓶頸。考慮到正確生成句子中的下一個字元所需的時間不斷增加,他意識到這項任務可能需要他的程式不斷地輸出字元,直到人類滅絕(假設所涉及的計算機能夠持續執行那麼長時間)。因此,在第二步中,庫格勒設計了一個程式,該程式使用先前確定的資料來推斷生成整個句子所需的字元數和計算時間。
庫格勒的計算表明,要讓 “生存還是毀滅,這是一個問題” 出現,需要極大的耐心:大約需要生成 2.68 x 1069 個字元,這將花費大約 2.95 x 1066 秒,或 9.35 x 1058 年。
由於我們宇宙的年齡估計為 138 億年,因此我們必須等待的時間幾乎是宇宙大爆炸至今這段時間的 7 x 1048 倍。而這一切僅僅是為了偶然產生《哈姆雷特》中的一句話。在這方面,西塞羅是對的:在有限的時間內,偶然性不太可能產生一首詩,甚至任何其他文字的一行可讀詩句。
本文最初發表於Spektrum der Wissenschaft,經許可轉載。
