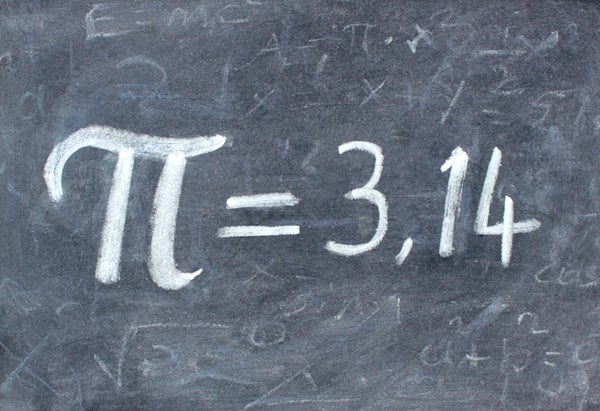用π(π)表示的數字用於計算任何涉及圓形(或近似圓形)的事物,例如圓形、球體、圓柱體、圓錐體和橢圓。它的值對於計算這些形狀的許多重要量是必要的,例如理解圓的半徑與其周長和麵積之間的關係(周長=2πr;面積=πr2)。
π也出現在確定橢圓面積以及求球體的半徑、表面積和體積的計算中。
支援科學新聞
如果您喜歡這篇文章,請考慮訂閱我們的獲獎新聞以支援我們 訂閱。 透過購買訂閱,您正在幫助確保有關當今塑造我們世界的發現和想法的具有影響力的故事的未來。
我們的世界包含許多圓形和近似圓形的物體;找到π的精確值有助於我們更準確地構建、製造和使用它們。
歷史上,人們對π只有非常粗略的估計(例如 3,或 3.12,或 3.16),雖然他們知道這些是估計值,但他們不知道這些估計值可能有多大的偏差。
對π的精確值的探索不僅帶來了更高的精度,還帶來了新概念和技術的發展,例如極限和迭代演算法,然後這些概念和技術成為新數學領域的基礎。
尋找π的實際值
在 3000 到 4000 年前,人們使用π的試錯近似值,而沒有進行任何數學運算或考慮潛在的誤差。最早關於π的書面近似值是巴比倫的 3.125(公元前 1900-1600 年)和古埃及的 3.1605(公元前 1650 年)。這兩種近似值都以 3.1 開頭——非常接近實際值,但仍然相對較遠。
尋找π的真實值的第一個嚴格方法是基於幾何近似。大約在公元前 250 年,希臘數學家阿基米德在圓的外部和內部都繪製了多邊形。測量這些多邊形的周長,可以得出包含π的範圍的上限和下限。他從六邊形開始;透過使用邊數越來越多的多邊形,他最終計算出了π的三位精確數字:3.14。大約在公元 150 年,希臘-羅馬科學家托勒密使用此方法計算出了 3.1416 的值。
大約在公元 265 年,中國數學家劉徽獨立地建立了另一個簡單的基於多邊形的迭代演算法。他提出了一種非常快速有效的近似方法,得出了四位精確的數字。後來,大約在公元 480 年,祖沖之採用了劉徽的方法,達到了七位精度。這項記錄保持了另外 800 年。
1630 年,奧地利天文學家克里斯托夫·格林伯格得出了 38 位數字,這是使用多邊形演算法手動實現的最高精度近似值。
超越多邊形
16 和 17 世紀無限級數技術的發展大大提高了人們更有效地逼近π的能力。無限級數是無限序列的項的和(或更少見的乘積),例如 ½、¼、1/8、1/16、… 1/(2n)。第一個關於可用於計算π的無限級數的書面描述是印度天文學家尼拉坎塔·索瑪亞吉在公元 1500 年左右用梵語詩句寫下的,其證明大約在公元 1530 年提出。
1665 年,英國數學家和物理學家艾薩克·牛頓使用無限級數,用他和德國數學家戈特弗裡德·威廉·萊布尼茨發現的微積分計算出 π 的 15 位數字。此後,記錄不斷被打破。1699 年達到 71 位數字,1706 年達到 100 位數字,1956 年達到 620 位數字——在沒有計算器或計算機幫助的情況下實現的最佳近似值。
在進行這些計算的同時,數學家也在研究π的其他特性。瑞士數學家約翰·海因裡希·蘭伯特 (1728-1777) 首先證明了π是一個無理數——它有無限多的數字,永遠不會進入重複的模式。1882 年,德國數學家費迪南德·馮·林德曼證明了π不能用有理代數方程表示(例如 π²=10 或 9π4 - 240π2 + 1492 = 0)。
追求更多π的數字
採用迭代演算法後,隨之而來的是對π更多位數的計算爆發,迭代演算法透過使用對先前值執行的計算來重複構建更新的值。一個簡單的迭代演算法示例允許您使用公式 (x+2/x)/2 逼近 2 的平方根
(2+2/2)/2 = 1.5
(1.5+2/1.5)/2 = 1.4167
(1.4167+2/1.4167)/2 = 1.4142,這已經是一個非常接近的近似值。
隨著電子計算機(20 世紀中期發明)中使用了類馬欽演算法(英國數學家 約翰·馬欽的公式 的推廣,該公式於 1706 年開發)和 高斯-勒讓德演算法 (18 世紀末),π的更多位數的進展得到了提升。1946 年,第一臺通用電子計算機 ENIAC 在 70 小時內計算出了 π 的 2,037 位數字。最近的計算發現了π 的超過 13 萬億位數字,耗時 208 天!
人們普遍認為,對於大多數涉及π的數值計算,十幾個數字就足以提供足夠的精度。根據數學家 約爾格·阿恩特和克里斯托夫·哈內爾 的說法,39 位數字足以執行大多數宇宙學計算,因為這是在原子直徑範圍內計算可觀測宇宙周長所必需的精度。此後,π的更多位數在計算中沒有實際用途;相反,今天對π更多位數的追求是為了測試超級計算機和數值分析演算法。
自己計算π
也有一些有趣而簡單的方法來估計π的值。最著名的方法之一是被稱為“蒙特卡羅”的方法。
該方法相當簡單。要在家裡嘗試,請在一張紙上畫一個圓,然後在它周圍畫一個正方形(如左圖所示)。假設正方形的邊長為 2,因此它的面積為 4;因此,圓的直徑為 2,其面積為π。它們的面積之比為π/4,約為 0.7854。
現在拿起一支筆,閉上眼睛,在正方形上隨機點點。如果你這樣做足夠多的次數,並且你的努力是真正隨機的,那麼最終你的點落在圓內的次數的百分比將接近 78.54%——或 0.7854。
現在,您已加入到歷代計算π的數學家的行列。
葉曉靜不為任何可能從本文中受益的公司或組織工作、諮詢、擁有股份或接受資金,並且除了上述學術任命外,沒有披露任何相關的附屬關係。