雷蒙德·斯穆裡安——邏輯學家、魔術師、數學家、謎題專家和道家哲學家——於去年去世,享年97歲。在他所從事的每項職業中,他都做出了重要的貢獻。但在他內心深處,從頭到腳,他都是一位演藝家。
在大型和小型聚會中,在朋友和陌生人之間,雷總是“在狀態”。如果有鋼琴,就會有音樂。如果有撲克牌,就會有魔術。如果有談話,就會有故事、笑話和令人困惑的悖論。
斯穆裡安對邏輯、知識、數學和生命的意義有重要的見解。為了向公眾傳播他的思想,他創作了大量的幻想、謎題和難題。我認為這些不僅僅是達到目的的手段。它們真的是他最大的快樂。教授講授——是為了讓演藝家能夠表演。
關於支援科學新聞業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞業 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和思想的具有影響力的故事的未來。
斯穆裡安應我的邀請多次來到史密斯學院,但我不能聲稱我真的認識他。我的結論基於他對職業的選擇、他的著作(尤其是回憶錄)以及其他人的回憶。在《四種人生:紀念雷蒙德·斯穆裡安》中,小提琴家克勞迪婭·謝爾寫道
我很快了解到,他到處都帶著一副撲克牌,不僅在餐廳表演魔術,幾乎在任何場合都表演,給那些發現自己在他附近的人們帶來微笑。他也非常樂意彈鋼琴。
他的論文學生之一羅伯特·考恩寫道
無論雷做什麼,無論是數學、謎題、音樂還是魔術,都以美和優雅為特徵。而且,它總是非常有趣。事實上,雷是終極演藝家;他總能給你帶來驚喜!
邏輯學家
在雷蒙德·斯穆裡安之前就存在邏輯謎題2,但他將這種型別提升到了藝術的高度。他的第一本謎題書《這本書叫什麼名字?》純粹是一種樂趣。謎題中充滿了騎士——他們總是說真話,以及騙子——他們總是說謊。
這是斯穆裡安的一個優雅謎題
我在騎士和騙子島上看到了一對。我問:“你們中有人是騎士嗎?” 其中一位回答了,從他的回答中,我知道了他是什麼樣的人,也知道另一個人是什麼樣的人。我發現了什麼?
答案在本專欄末尾。
在對騎士和騙子進行各種變化之後,他發現他的一些角色是理智的,並且看到世界本來的樣子,而另一些角色是瘋狂的,並且看到世界不是本來的樣子。當這種謎題的可能性被窮盡後,我們發現騎士和騙子說的是未知的語言。這是斯穆裡安最巴洛克的謎題之一
我在特蘭西瓦尼亞,那裡的人類說真話,吸血鬼說謊。有些人是理智的,有些人是瘋狂的。“bal”和“da”這兩個詞要麼表示“是”和“否”,要麼表示“否”和“是”。為了逃離德古拉,我必須找到一個句子S,它可以解開所有秘密,也就是說,對於任何陳述P,如果你問任何人(人類或吸血鬼,理智或瘋狂)
P為真當且僅當S為真是否成立?
如果P為真,他們會回答“Bal”,如果P為假,他們會回答“Da”(無論“bal”實際上是什麼意思)。
我找到了這樣一個句子。你能找到一個嗎?
通常,斯穆裡安的謎題書都有一個議程。這些書中有不少以哥德爾不完備性定理及其著名的困難證明結尾。斯穆裡安的許多數學貢獻都集中在哥德爾和塔斯基的工作上。我個人的感覺是,這些謎題對於理解或解釋哥德爾的工作並沒有特別大的幫助。但這是一種教學判斷。如果我將這些謎題視為數學結構本身,它們是非常有趣的。
這裡有一個最好的謎題,以簡化的形式:為了他的證明,哥德爾產生了一個句子,這個句子是真的,但無法透過建立一個句子來證明,這個句子實際上說:
“你無法證明我!”
哥德爾的證明中有很多令人驚歎的想法,但最令人驚歎的是(對我而言)不知何故,這個句子成功地指代了自身。斯穆裡安創造了一種非常簡單的語言來做到這一點。
考慮所有由字母N、P和R組成的單詞(即,所有符號串)。以下是如何解釋這種語言中的句子

現在假設可證明性和真理是一樣的。考慮句子
NPRNPR。
開頭的NP表示該句子在說
“RNPR無法證明。”
但是RNPR是NPR的重複,即NPRNPR。換句話說,這個句子說
“你無法證明我!”
由此可見,在這種語言中,證明和真理並不一致,因為那將意味著NPRNPR為真當且僅當它無法被證明。
在任何意義上,這都不是哥德爾定理。但它非常有趣。
謎題專家
斯穆裡安豐富的謎題書確立了他作為謎題大師的地位。他的天賦在早年就顯現出來了。作為一名高中生,斯穆裡安發明了一種新的謎題形式。很久以後,他才發現這種形式已經存在:逆行分析。逆行分析問題在棋盤上呈現棋子,並詢問有關使棋子到達您所看到位置的遊戲的資訊。不涉及國際象棋策略。問題完全是關於國際象棋規則的邏輯。這是一種非常有吸引力的謎題形式,斯穆裡安的貢獻非常巧妙、富有想象力且令人驚訝。
這是我最喜歡的謎題,它出現在他的第一本逆行問題書《夏洛克·福爾摩斯國際象棋之謎》的封面上
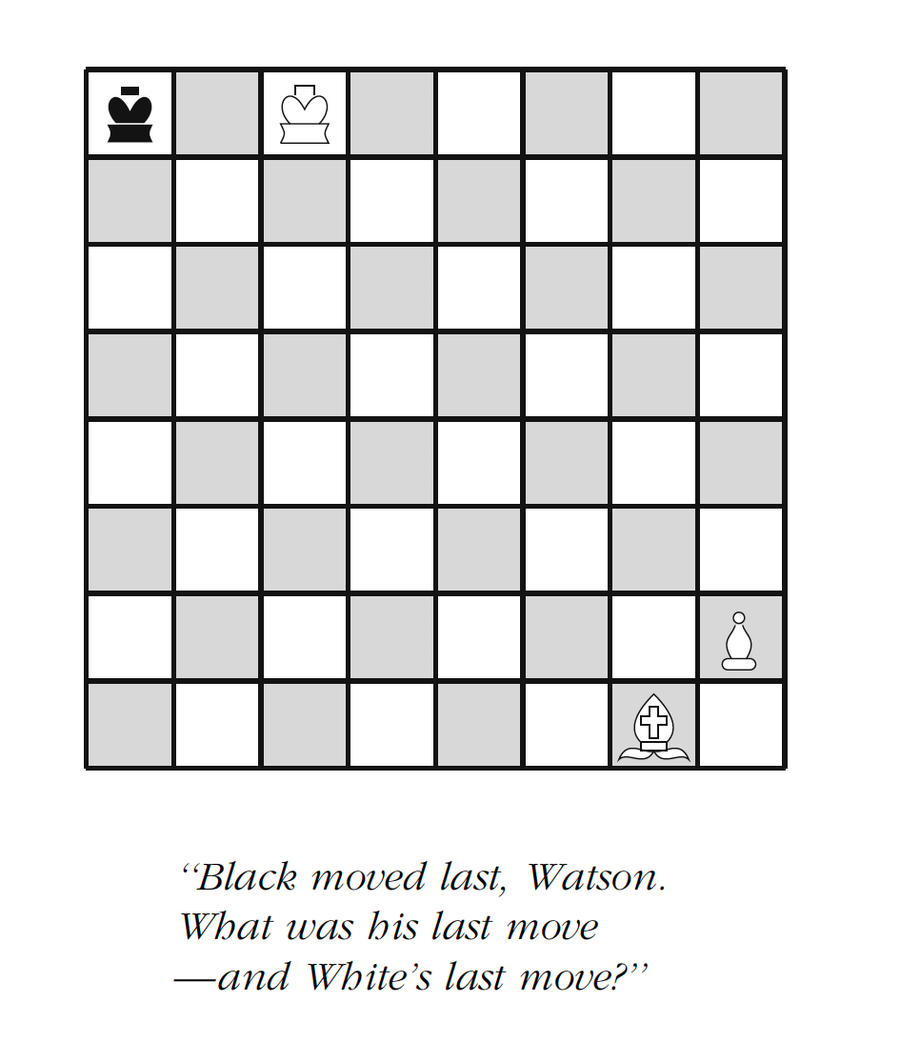
來源:詹姆斯·亨勒
黑方的最後一步一定是王向上走了一格,但這怎麼可能呢?他本應受到白方主教的將軍,而且似乎沒有任何方法可以使白方將黑方國王置於將軍之中。除非國王已經處於將軍之中,否則主教不可能移動到它所在的位置,這不可能。使棋子處於將軍狀態的唯一另一種方法是顯現將軍,也就是說,某個位於國王和主教之間的棋子移開了,顯現了將軍。但是棋盤上沒有白方棋子可以顯現將軍!
答案在本專欄末尾!
這是另一個謎題,據報道是斯穆裡安本人最喜歡的謎題。它出現在他的第二本逆行書《阿拉伯騎士國際象棋之謎》的封面上
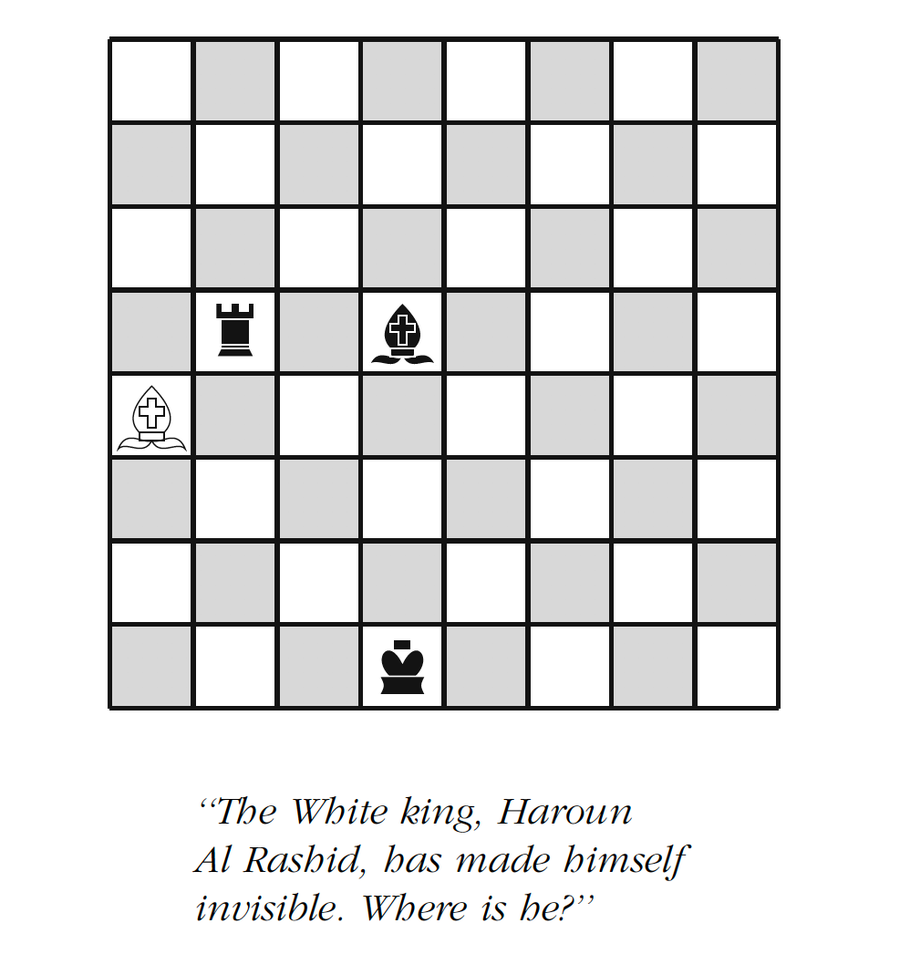
來源:詹姆斯·亨勒
數學家
斯穆裡安的一本謎題書《撒旦、康托爾和無窮大》,以康托爾的對角線證明作為高潮,證明實數集是不可數的,也就是說,不存在從自然數到十進位制數集的對映。我認為,在這裡,斯穆裡安為教學做出了重大貢獻。
像許多數學家一樣,我記得我聽到康托爾證明的那一刻,就是我知道我想成為一名數學家的那一刻。因此,我以某種方式向無數學生揭示了它。但是每次(直到我讀了《撒旦、康托爾和無窮大》),至少會有一個學生被某個特定的點困住。
我通常以我的十一年級老師奧恩多夫小姐向我展示的方式來呈現這個證明。假設存在從自然數到十進位制數的對映。奧恩多夫小姐寫下了這樣一個對映的開始,只使用了0到1之間的十進位制數。

然後,她構造了一個不在對映範圍內的十進位制數,方法是選擇一個數字,該數字的位數與對角線上的位數不同,
.png?w=900)
她解釋說,這樣的數字,比如0.2759...,不可能是範圍內的第一個數字,因為它具有不同的第一位數字。它也不可能是範圍內的第二個數字,因為它具有不同的第二位數字,依此類推。因此,該數字不在範圍內,因此自然數集和十進位制數集之間不存在對映。
每當我展示這個證明時,總會有人抱怨:“但是你可以將這個數字新增到列表中!你可以建立一個包含它的對映!”
斯穆裡安極其有趣的改編版本避免了這個問題。他講述了一個關於撒旦的故事。他想象撒旦戲弄到達地獄的靈魂。他向一個靈魂提供了一個交易:他,撒旦,將在紙上寫一個自然數。在地獄的每一天,受詛咒的靈魂都可以嘗試一次猜測這個數字。如果靈魂說出了這個數字,它就會被釋放並升入天堂。如果沒有,它可以第二天再猜。
很容易看出,有一種逃離地獄的策略。你只需猜測:第一天猜0,第二天猜1,然後猜2,依此類推。
撒旦以這種方式失去了靈魂,所以他改變了遊戲規則。現在他寫的是正整數或負整數,供被譴責者猜測。但是,再次有一種逃脫策略。靈魂可以按以下順序猜測整數:0、1、-1、2、-2、3、-3、...。
撒旦第二次改變了遊戲規則。現在他寫的是分數。但是,與自然數和整數一樣,也有一種策略。玩這個遊戲的靈魂可以首先執行完分子和分母都小於2的所有分數。然後,靈魂可以命名分子和分母都小於3的其他分數,依此類推。
在每種情況下,都有一種策略可以保證在有限的天數內逃脫。此外(這裡很重要的一點),即使在魔鬼選擇他的數字之前告訴他策略,靈魂仍然會在有限的天數內逃脫。
最後,撒旦最後一次改變了遊戲規則。現在他寫的數字是無限十進位制小數。現在沒有任何策略會奏效。與自然數遊戲、整數遊戲和分數遊戲不同,如果魔鬼被告知策略,如果他被告知將要猜測十進位制小數的順序,他可以(使用康托爾的技巧)寫下一個靈魂永遠猜不到的十進位制小數。
我現在在教這個證明時使用這種方法。這很有趣。它是

來源:詹姆斯·亨勒
相同的證明,但簡報有一種整理量詞的方法。
魔術師、哲學家和講故事的人
斯穆裡安的第一份工作是表演魔術。這在他高中畢業之前。他是一位“近距離”魔術師,而不是舞臺表演者。最終,魔術成為了他的副業。但非正式地,魔術是他興趣的統一主題。例如,正是數學的魔力吸引了他。
除了數學之外,悖論形式的魔術也是斯穆裡安邏輯的核心,也可以說是他哲學的核心。他熱愛悖論。當他發現一個悖論時,他會培育它、逗弄它並祝福它。我懷疑是悖論將他吸引到了道教。
一個豐富的悖論也是一個好笑話。斯穆裡安喜歡好笑話。斯穆裡安的講座,尤其是在他晚年,很像單口喜劇。
依然是演藝家
雷蒙德·斯穆裡安的藝術至少可以在兩個層面上欣賞。在一個層面上是與他的謎題搏鬥的樂趣。這種樂趣可能是有限的。但還有一個更深層次的層面。斯穆裡安的謎題啟發我們中的一些人創作自己的謎題。完全披露:我和我的合著者在我們的邏輯書中灑滿了騎士和騙子。撒旦也在那裡。
我是兩個層面的鑑賞家。我提交以下證據
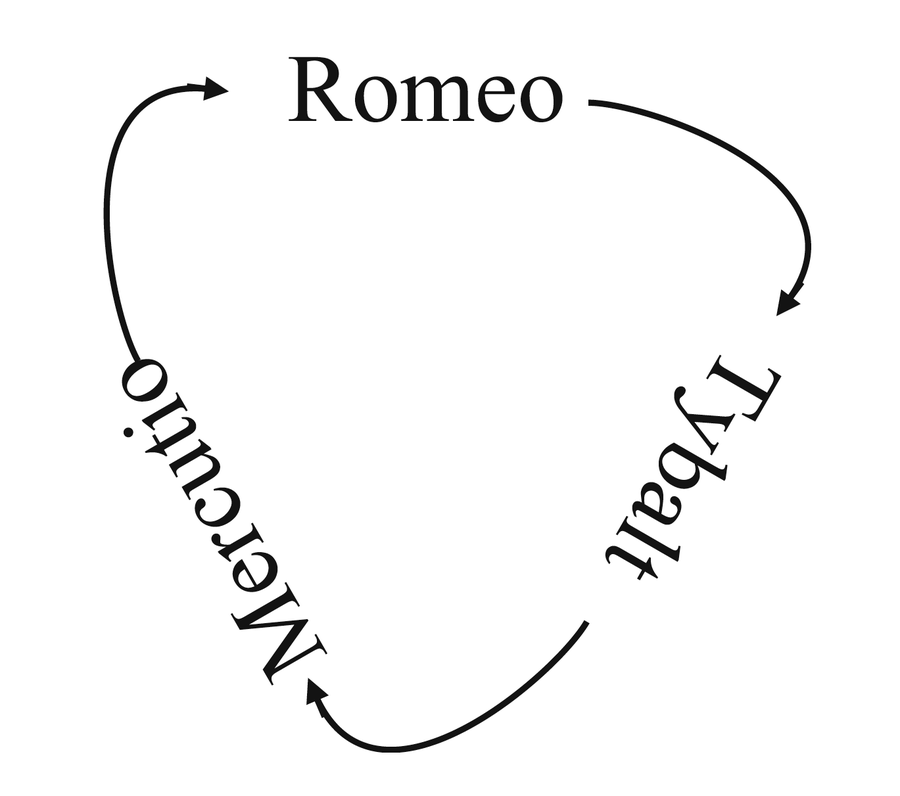
來源:詹姆斯·亨勒
在維羅納市的一個區,只有騎士和騙子。所有這些都是蒙太古或卡普萊特。三位居民,羅密歐、墨丘西奧和提伯爾特,圍成一圈互相交談。這幾位紳士不是《羅密歐與朱麗葉》中的人物,因此他們的家族不一定是莎士比亞筆下的人物。每個人都指向他左邊的人,並說明了他的家族(蒙太古或卡普萊特)和型別(騎士或騙子)。
每個人都對他的鄰居給出了相同的描述。提伯爾特對羅密歐關於墨丘西奧的說法提出異議。你能從中推斷出什麼?
在這三個人中,至少有兩個人必須來自同一個家族。如果我補充說墨丘西奧和羅密歐來自同一個家族,你還能說什麼?
我的學生之一加布裡埃爾(加比)·曼納也在這個更高層面上欣賞斯穆裡安的作品。她寫了一系列謎題,涉及一個功能失調的家庭,該家庭每週按時間表說真話或說謊
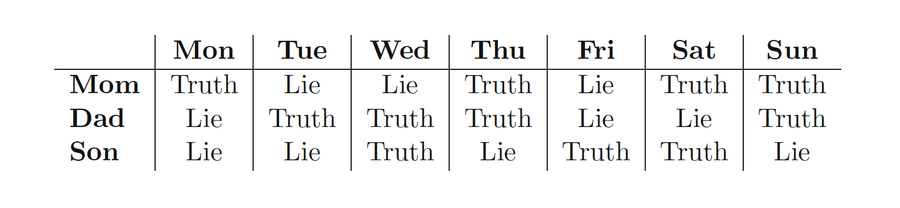
兒子工作日和母親住在一起,週末和父親住在一起。以下電話對話發生在工作日。加比要求你確定今天是星期幾。
爸爸:約翰尼這個週末會和你在一起,因為我要出差三天。我昨天告訴他要告訴你這件事。
媽媽:不,你什麼也沒告訴他,而且你也不會出差。為了證明這一點,我要問他。[她對著兒子喊道。] 約翰尼,昨天你爸爸有沒有告訴你任何關於即將到來的週末的事情?
兒子:[進來] 是的,他昨天說了。他說他這個星期六會晚一個小時來接我。
媽媽:你在撒謊。我知道你爸爸沒有向你提及任何關於週末的事情。爸爸:是的,我說了!我昨天告訴他了!
我非常喜歡斯穆裡安的逆行國際象棋問題。這是我最近整理的一些東西

來源:詹姆斯·亨勒
許多逆行問題涉及國王同時受到兩個不同棋子將軍的情況。使用仙靈棋子,這個數字可以增加,例如:♗ 是反射主教。它的移動方式類似於主教,但可以從棋盤的側面反彈。三個棋子同時將軍國王是我使用反射主教所能做到的最好的。問題似乎是 8 是偶數。我不認為我能對此做些什麼。但是,在 7 x 7 棋盤上,我可以設法進行四次同時將軍。
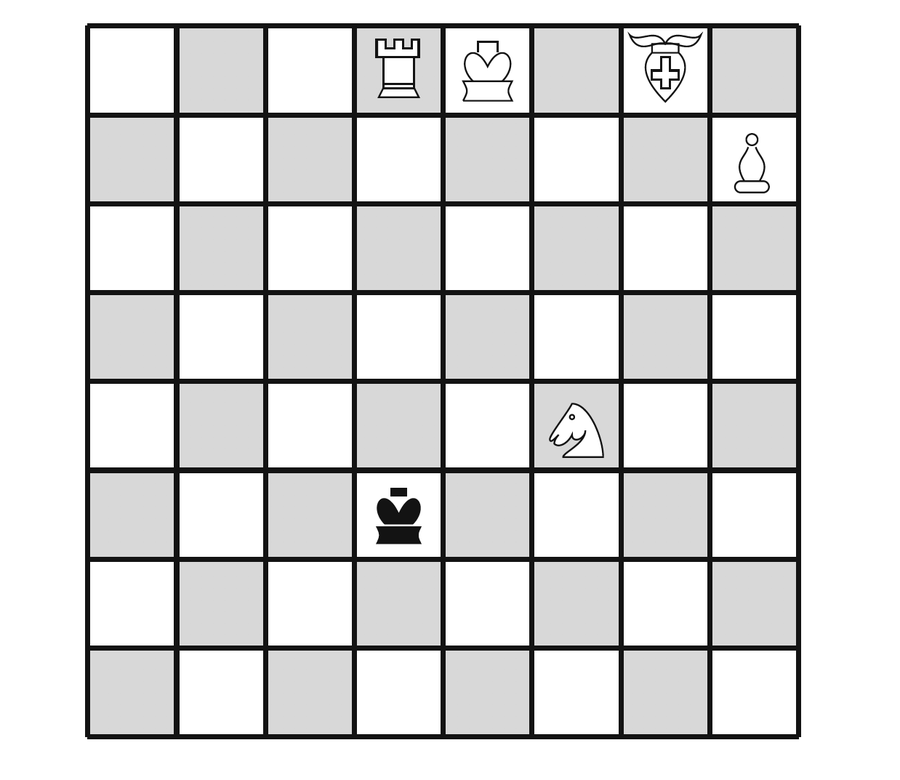
來源:詹姆斯·亨勒
斯穆裡安的撒旦故事也激發了我的謎題創作傾向。這是我在邏輯課程第一學期的期末考試中提出的一個問題
魔鬼為受詛咒的靈魂提供了一項新交易。他給他們進行論文測試。只有一個問題。撒旦將答案寫在一張紙上,並將其放在口袋裡。他不會改變它。但他沒有告訴你問題!你必須寫一個你不知道的問題的答案!而且答案必須與他寫的一模一樣!他甚至不會告訴你它有多少頁(難道你不討厭這樣做的教授嗎?)!
如果你成功了,你就會升入天堂。如果沒有,那麼你第二天再試一次。順便說一句,你不知道魔鬼用什麼語言寫了他的答案。它確實使用了羅馬字母。
兩個答案
對於第一個騎士和騙子問題
答案是“否”。這告訴你說話者是一個騙子,因為騎士會回答“是”。此外,它告訴你另一個人是騎士,因為如果他是騙子,回答的騙子會說“是”。
對於第一個國際象棋問題
的確,棋盤上沒有白方棋子可能顯現將軍。但可能曾經有。黑方國王可能已經吃掉了這樣一個棋子,一個騎士。事實上,這一定是兩個回合前棋盤的樣子
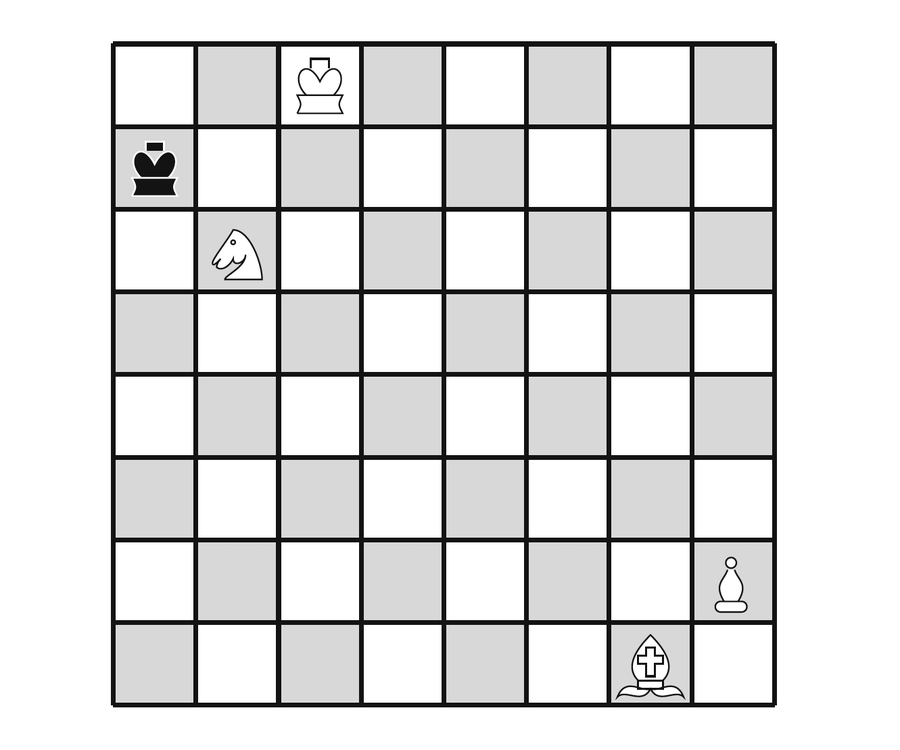
來源:詹姆斯·亨勒
所有其他謎題的答案都可以在www. math.smith.edu/*jhenle/Pleasingmath/找到。
讀者可以將評論和新謎題傳送給我,地址為 pleasingmath@gmail.com。
