即使數學令人費解,它也是美麗的。攝影師傑西卡·溫妮在 2018 年開始拍攝世界各地數學家的黑板時,就著手捕捉這種魅力。“我一直對進入我知識領域之外的世界感興趣,”溫妮說。在不理解黑板上的數學代表什麼的情況下,她能夠在純粹的審美層面上欣賞它。“這與我觀看抽象畫時的感覺相似。但它增加了更多的趣味,因為在表面之下有偉大的意義和偉大的深度,他們正試圖揭示普遍真理。”
當溫妮與兩位在她科德角避暑別墅附近度假的數學家成為朋友時,她第一次被數學世界所吸引。當她瞭解他們的研究時,她發現數學過程和藝術過程之間有許多相似之處。“我真的很驚訝地看到他們如何工作以及他們所做的事情是多麼有創意,”她說。
隨著溫妮開始前往不同的大學會見更多的數學家,她發現他們的黑板風格是多麼多樣化。“有些非常乾淨整潔,並且經過非常仔細的考慮,”她回憶道。“而有些則只是這種爆發和混亂。黑板幾乎感覺像是人物的肖像,並且取決於數學家的個性。”
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的有影響力的故事的未來。
許多照片將收錄在《不要擦除:數學家和他們的黑板》一書中,該書將於 6 月由普林斯頓大學出版社出版。溫妮打算繼續這個專案,尤其因為她的旅行因疫情而中斷。她原計劃參觀劍橋大學的數學系,直到她得知他們的黑板都已被白板和數字板取代。“我非常喜歡在黑板上工作的模擬性質,”她說。“我注意到很多地方都在擺脫他們的黑板,我感到有記錄這一點的緊迫性。”

致謝:傑西卡·溫妮
混合高斯分佈
物理測量(例如從人群中隨機選擇的女性的身高)通常會產生一種稱為高斯分佈的分佈,其圖看起來像一座圓潤的山峰。機器學習演算法通常會獲得異構資料(例如,隨機女性和男性的身高),一項具有挑戰性的任務是將測量結果分解為兩個或多個組成部分。麻省理工學院的安庫爾·莫伊特拉和他的同事們發現了一種分離曲線的方法,該方法僅需要混合物的頭六個“矩”——特殊特徵。“我在黑板上畫的是我們論文中的關鍵證明,”莫伊特拉說。“事實證明,這等同於能夠取兩個不同的混合物,將它們相減,並表明結果函式最多穿過零軸六次。”
致謝:傑西卡·溫妮
分支波
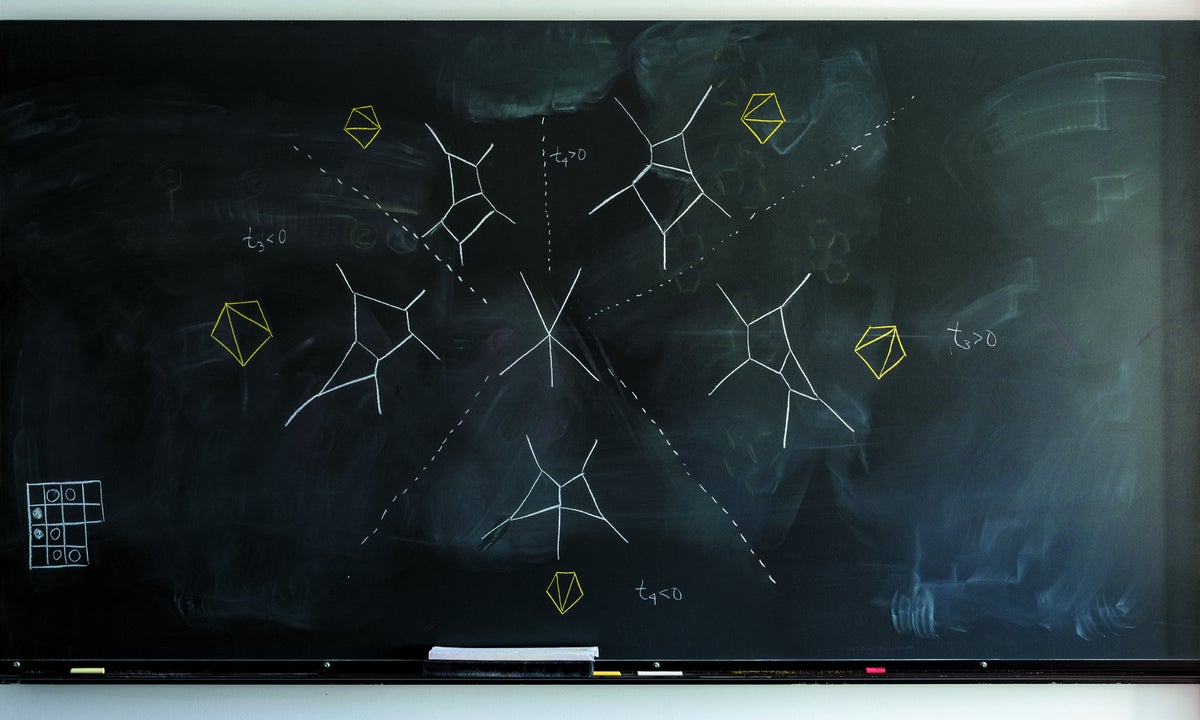
類似火柴人的圖表代表了波演化的快照。白色線條編碼了特定時刻淺水波配置的波峰位置。“這些波具有有趣的相互作用,”哈佛大學數學家勞倫·K·威廉姆斯解釋說。“例如,兩個波可以相遇並形成一個波出來,如果讓時間變化,就會看到不同的波相互作用模式。” 威廉姆斯和她的合作者俄亥俄州立大學的 Yuji Kodama 使用這些圖表來研究所謂的 Kadomtsev-Petviashvili (KP) 方程的解,該方程描述了波的行為。他們發現,由某一類解產生的波模式可以透過多邊形的三角剖分(黃色)進行分類。“如果稍微改變解的引數,這些波模式可能會退化並形成,例如,中心顯示的白色‘海星’圖案,”她說。左下方是 Kodama 和 Williams 稱之為“圍棋圖”的東西,以棋盤遊戲圍棋命名,他們用它來研究 KP 方程的某些解。

致謝:傑西卡·溫妮
外出散步
每條彩色線都顯示了行人在這個“頂點模型”中穿過正方形網格的路徑。行人的路徑不能重疊,因此每當兩個人相遇時,他們都必須決定每個人將走向哪個方向。該決定可能存在偏差——例如,與顏色較暖的步行者相比,顏色較冷的步行者可能更傾向於向東而不是向北走。“儘管它的描述很簡單,但它的大規模行為是複雜的,並且與許多數學和物理現象密切相關,”麻省理工學院的數學家阿列克謝·博羅丁說。頂點模型可以擴充套件到包括更多的步行者和更多的顏色。“欺騙性的簡單性、隱藏的深度以及數學在分析中的有效性使這個系統對我很有吸引力。” 博羅丁還喜歡“美學因素”,他補充道。
致謝:傑西卡·溫妮
有組織的混亂
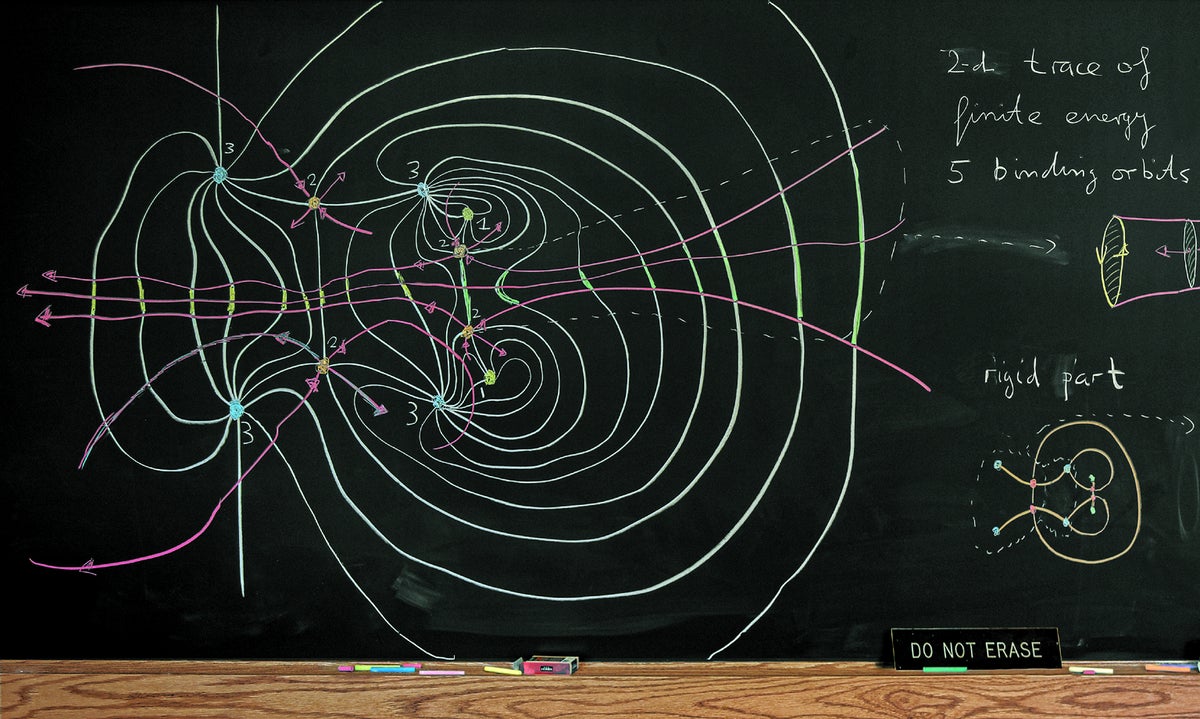
事實證明,混亂中可能存在秩序。在 1999 年至 2003 年間,新澤西州普林斯頓高階研究所的赫爾穆特·霍費爾和他的同事們開發了一個研究這種秩序的領域,稱為辛動力學。霍費爾的黑板描繪了“有限能量葉理”(白色線條)——用於表徵動力學系統(例如在地球和月球之間移動的衛星)中混亂的工具。這個複雜的表面系統與衛星的位置和動量隨其與兩個行星體的引力相互作用而演變有關。霍費爾希望“這種對混亂的更好理解最終將應用於航天任務的設計”。例如,早期的努力利用了關於混亂的見解來節省太空探索期間的燃料,但代價是增加了旅行時間。霍費爾認為,這項新工作可以進一步提高燃油效率,而不會延長任務的持續時間。
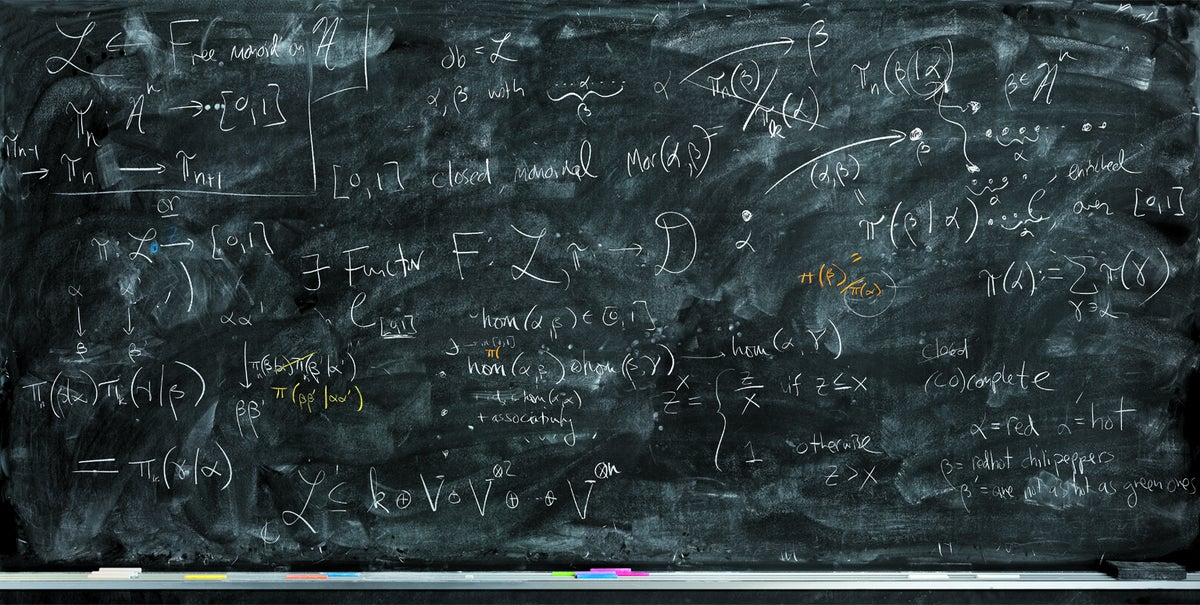
致謝:傑西卡·溫妮
匹配形狀
根據拓撲學的數學領域,咖啡杯和甜甜圈是著名的“相同”形狀,拓撲學根據表面包含的孔洞數量對其進行分類。因為咖啡杯和糕點都只有一個孔,並且可以彎曲和拉伸成相同的形狀而無需進行任何切割或穿孔,所以它們在拓撲上是相同的。同樣,標記為“2”的兩個表面以及標記為“6”的表面在根本上是相同的。“它們非常有趣,”新澤西學院的數學家南希·欣斯頓說,她在微分幾何學中研究此類形狀上的路徑。
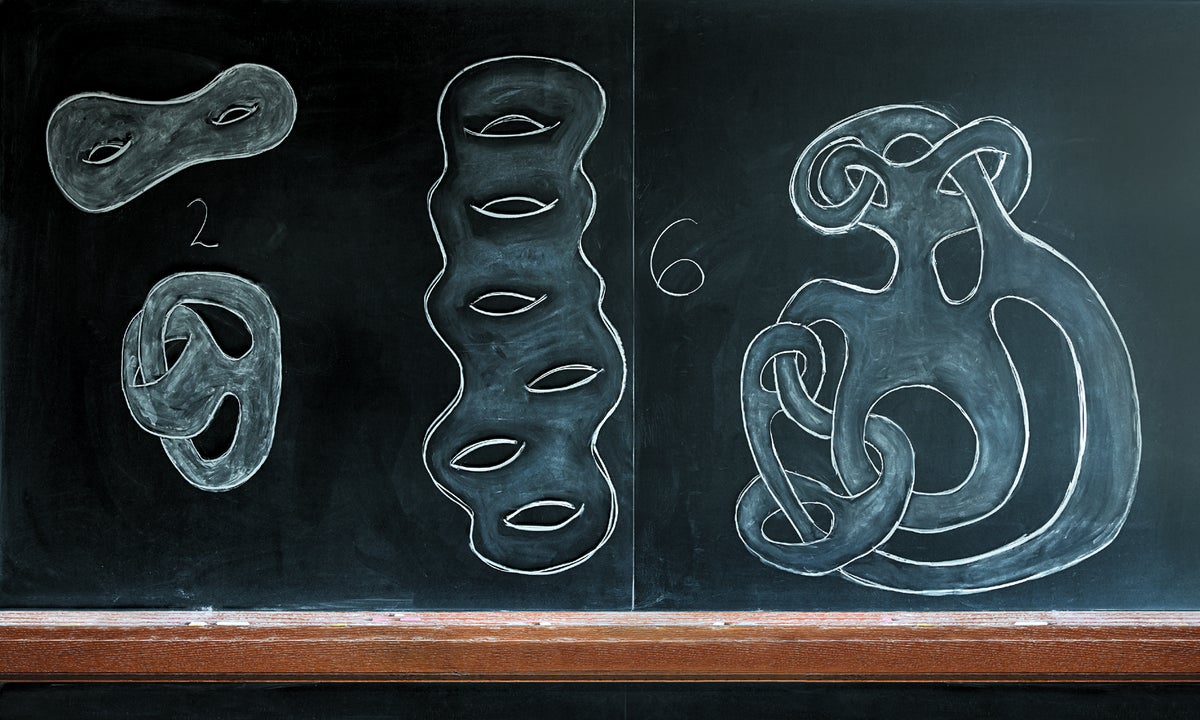
致謝:傑西卡·溫妮
合作
黑板通常是數學合作的最佳工具——視覺和觸覺場所,可以融合兩個人的想法和直覺。皇后學院的數學家約翰·特里拉和 X,月球工廠的 Tai-Danae Bradley 試圖理解自然語言中隱藏的數學結構。“那是我們第一次談到以特定方式形式化這種結構,”特里拉說。“我和泰伊在黑板上一起工作,它顯示了我們兩個人的寫作。例如,大的‘存在[用 表示]函子 F’是我的;下面的‘hom(alpha, beta) in [0,1]’是泰伊的。” 這項研究是特里拉尋找“幕後工作以瞭解正在發生的事情”的總體探索的一部分,他說。“在抽象層面上升一級來解釋某些事情有點像特意爬山環顧四周——在研究中很有用,因為它可以顯示在未知領域的前進方向。”

致謝:傑西卡·溫妮
解碼拓撲學
特里拉和布拉德利還與數學家和資料科學家泰勒·布賴森合作編寫了教科書《拓撲學:分類方法》。他們討論瞭如何最好地呈現材料,他們的黑板代表了他們旨在傳達的一些內容。“上面的內容不是研究——它都是典型的博士生在拓撲學課上會學習的標準數學,”特里拉說。
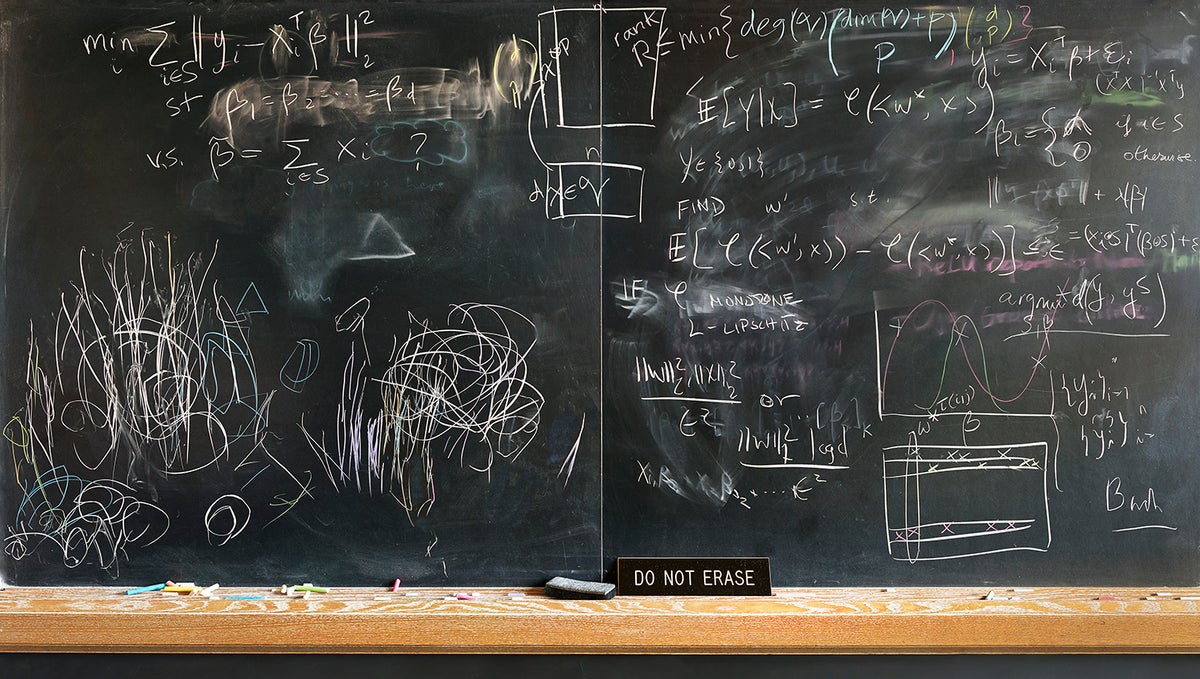
致謝:傑西卡·溫妮
進行中
密歇根大學電氣工程師和計算機科學家勞拉·巴爾扎諾研究機器學習和訊號處理的數學模型。“在特別的一天,我和兩位學生和一位同事分享了關於幾個不同問題的想法,”她回憶道。“事實上,現在黑板左上角的部分對我來說幾乎沒有意義。黑板右下角的部分是我一年後仍在研究的東西,幾乎沒有任何進展。右側黑板的其餘大部分內容現在已經發表了!” 對於外行人來說,左下角最後一部分可能與其餘部分一樣難以理解,但巴爾扎諾說,那部分是她當時 2.5 歲的女兒畫的。“粉筆是讓她保持專注的好方法——至少 15 分鐘。”

致謝:傑西卡·溫妮
無限度對映
從一個函式開始,或 f, 用複數定義,或 z。當一個數是複數時,這意味著它包含一個虛部——即 -1 的平方根。然後迭代函式的連續版本 z 以建立函式的軌道。接下來取接近 z 的點並檢視它們的軌道。此過程描述了該函式的動力系統。紐約市立大學研究生中心的數學名譽教授琳達·基恩對無限度函式的動力系統感興趣。“我對無限度對映很感興趣,”基恩說。“這些圖片旨在幫助理解當您更改無限度的 f 時會發生什麼。”

