數學家們今年非常忙碌:他們發現了迄今為止最大的素數,一個新的圓周率公式,約翰·塞巴斯蒂安·巴赫音樂中的神秘模式,甚至一種全新的新型形狀。其中一些發現是實用的——例如,新發現的形狀出現在自然界中,並已被用於創意建築設計。另一些,例如 4100 萬位數的素數,用處不大——但都令人著迷。以下是我們今年撰寫的一些最令人興奮的數學發現。
新形狀問世
一位數學家想知道,一個形狀最少需要有多少個角才能仍然能夠無縫隙地完全覆蓋一個表面。這個難題促使他和他的同事們發現了以前從未在數學上描述過的形狀,稱為軟細胞。雖然軟細胞對數學家來說是新的,但事實證明,軟細胞存在於鸚鵡螺殼、紅細胞和自然界的其他元素中。
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您將有助於確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
超長素數
素數——只能被 1 和自身整除的數字——長期以來一直讓數學家著迷。今年,一位研究人員發現了已知的最大素數,它擁有驚人的 41,024,320 位數字。自上次發現新的素數以來已經過去了六年,而且搜尋變得越來越困難,因為素數隨著它們的增長而彼此之間分佈得更遠。
圓周率新公式
圓周率 (π) 的概念,即圓的周長與其直徑的比率,自古代巴比倫以來,4000 年來一直廣為人知。但是,計算這個無理數的精確位數一直是一個挑戰。最近,物理學家使用弦理論提出了一種全新的計算圓周率的方法。
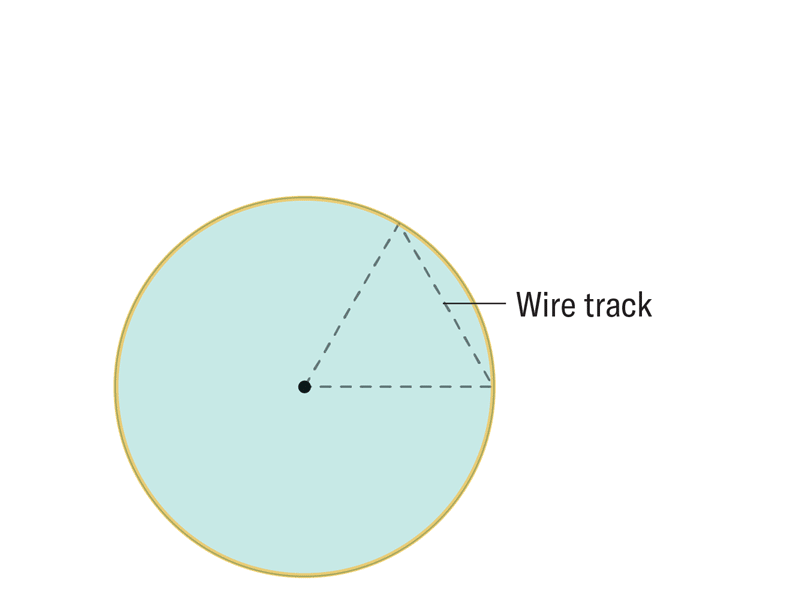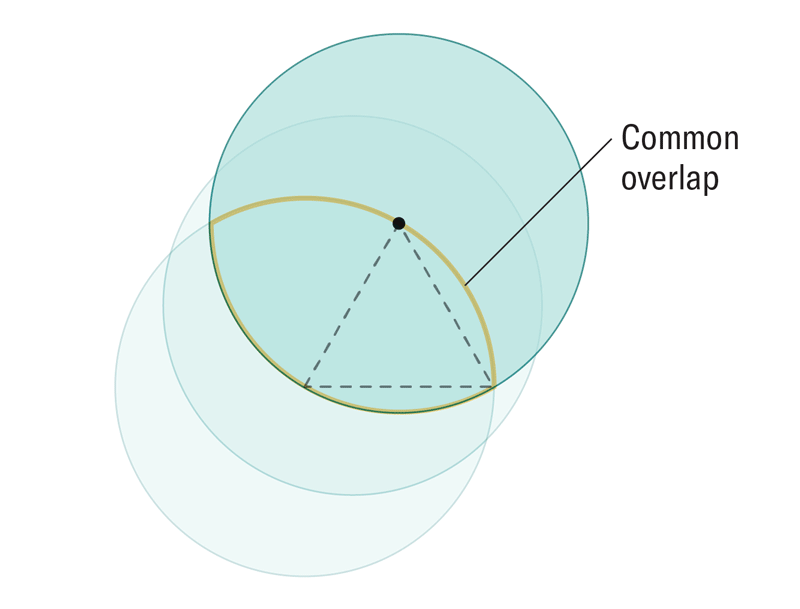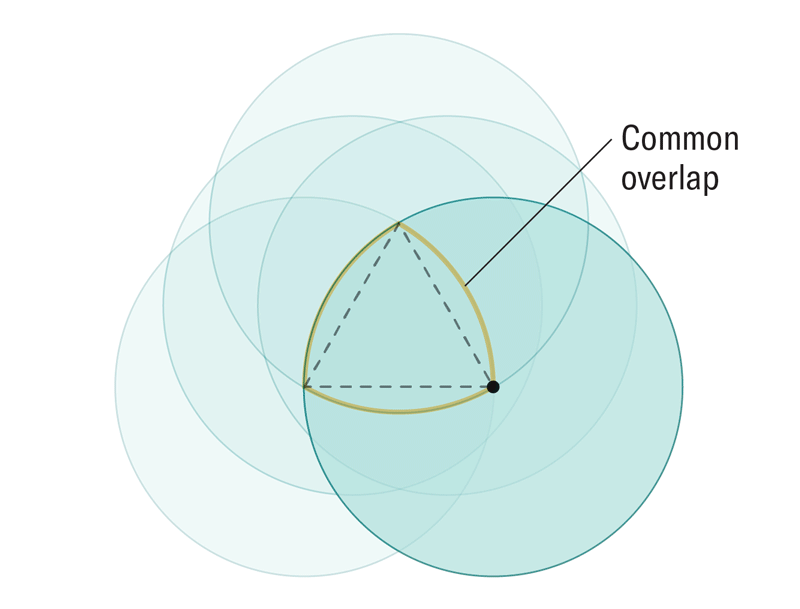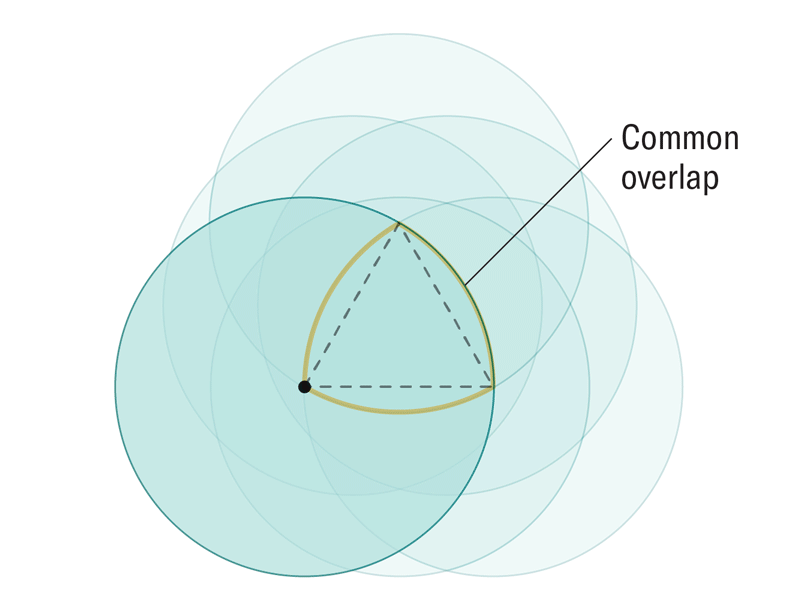
阿曼達·蒙塔內斯
多維度輪子
40 年來,數學家們一直在思考一個問題:我們如何在任何維度中找到具有最小體積的等寬形狀?研究人員最近設想了一種新型的多維輪子來回答這個問題。這種新型輪子可以在任何維度上構建,其尺寸僅為傳統滾動形狀(如圓形或球體)的一小部分。
計算不可計算之物
這項突破與數學中的一個基本真理有關:並非所有事物都可以計算,無論人們多麼努力(或海狸多麼忙碌)。一種特殊的不可計算表示式稱為忙碌海狸函式。它的值,稱為 BB(n),對於所有數量的 n 永遠不會被知道,但一個名為“忙碌海狸挑戰”的國際合作專案最近成功確定了該函式的第五個值——這讓認為這不可能的數學家們感到驚訝。

巴赫的鍵盤樂器前奏曲樂譜。
PFMphotostock/Getty Images
J. S. 巴赫的隱藏資訊
科學家們將巴洛克作曲家約翰·塞巴斯蒂安·巴赫創作的樂譜轉化為數學網路,並分析了他的不同風格的變化。他們使用資訊理論來查詢他音樂中的模式,這些模式有助於解釋巴赫如何透過他的作品傳達資訊——包括音樂、數學和情感資訊。
缺失的瓷磚
數學家們長期以來一直想知道,是否有一種單一的形狀可以鋪滿一個表面——也就是說,完全覆蓋一個平面——而不產生重複的圖案。許多人懷疑是否存在這樣一種形狀,即所謂的愛因斯坦瓷磚,但研究人員最終發現了一種。雖然這種瓷磚是在 2023 年宣佈的,但參與其中的一位數學家今年向我們講述了幕後故事。
