在20世紀70年代早期,數學家唐納德·克努特與他的妻子在挪威度過了一個學術休假。這段時間本應是用來放鬆的。然而,一天晚上,他驚醒了他的伴侶,情緒激動。他迫切需要寫一本書。他向他的配偶保證,別擔心,只需要一週時間。為了專心寫作,他在奧斯陸為自己預訂了一間酒店房間。
在那裡,他起草了後來成為超現實數:兩位前學生如何轉向純粹數學並找到完全的幸福的書。儘管克努特並沒有發明超現實數的概念,但他卻是第一個發表關於該主題的詳細著作並創造了這個術語的人。時至今日,他的書仍被認為是該主題的標準著作。
然而,這部著作絕非普通的非小說類作品。它由兩個虛構人物愛麗絲和比爾之間的對話組成。書中還介紹了超現實數的真正發明者,已故的數學家約翰·霍頓·康威,他於2020年去世。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保未來能夠繼續講述關於發現和塑造我們當今世界的想法的具有影響力的故事。
“起初,一切皆為空虛,J.H.W.H. 康威開始創造數字,”克努特寫道。克努特在康威的名字中添加了額外的首字母,以暗示四字神名(希伯來語中上帝的四字名字,音譯為 YHWH 或耶和華),他在 Numberphile 的 YouTube 影片中解釋道。
這絕非唯一的聖經典故;甚至克努特撰寫這本書的背景故事也呼應了宗教創世故事。他只用了一週的時間就把整本書寫成了文字,正如他向妻子承諾的那樣。“在第六天我完成了它。在第七天我休息了,”克努特告訴 Numberphile。
超現實數是透過在兩個給定的現有數字之間新增值來建立的。例如,如果您檢視 0 和 1,則 1/2 在中間,1/4 在 0 和 1/2 之間,依此類推。這種方法使得越來越精確地解析數軸成為可能。
這個想法乍聽起來並不引人注目,但是,與簡單地提供分母越來越大的分數不同,在某個時刻,一切都會爆炸,突然之間,出現了甚至不包含在實數中的值。
兩個公理產生一個不可思議的數字宇宙
康威建立了兩個基本規則,從中產生了不可估量的數字領域。每個數字 x 由兩個集合 ML 和 MR 定義,它們包含先前建立的數字:x = {ML : MR}。
ML 是左手集,MR 是右手集。第一個規則是左手集的元素始終小於右手集的元素。
第二個規則規定,0 是由兩個空集界定的數字。這兩個規則為數學的一個極其多樣化的分支奠定了基礎!

超現實數 x 來自於位於兩組數字 ML 和 MR 之間的值。 來源:Manon Bischoff/Spektrum der Wissenschaft,由 Amanda Montañez 重新設計
在這些基礎之上,克努特的超現實數創世故事發生在幾天之內。在第零天,根據第二條規則,0 從無到有地被創造出來,他將其表示為 0 = { : }。
在第一天,又建立了兩個數字:1 = {0: } 和 –1 = { :0}。這兩個數字之所以出現,是因為它們是數軸上第二大和第二小的整數(分別是)。
超現實創造的第二天變得更加有趣。現在你可以第一次使用不同的數字了。例如,{0:1} 表示介於 0 和 1 之間的數字,即 1/2。你也可以建立 {1: } = 2, {–1:0} = –1/2 和 { :–1} = –2。
以這種方式繼續下去,在第三天,你將得到 1/4、3/4、3 等等。
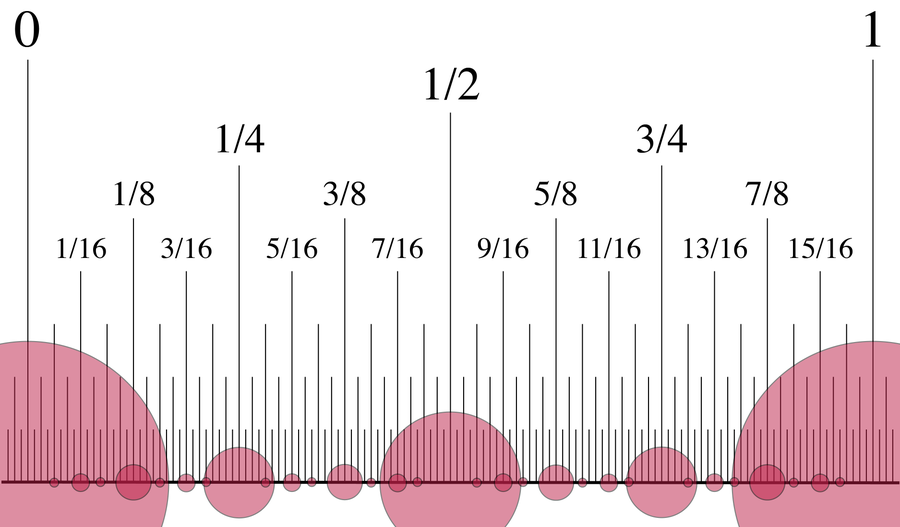
分母為 2 的倍數的分數在超現實數的建立中逐漸出現。 來源:David Eppstein/Wikimedia Commons(CC0 1.0)
如果你堅持下去,到第 n 天,你將擁有從 –n 到 n 的所有整數,以及分母為 2, 22, 24, 28,... 到 2n 的所有分數。這種分母是 2 的倍數的分數稱為二進有理數。這使得超現實數看起來相當枯燥:它們僅由整數和二進有理陣列成。沒有 π (π) 或根號二 (√2) 等值的蹤跡——甚至連像 1/3 這樣微不足道的數字也沒有。
所有實數的黎明
超現實數真正令人興奮的特性在你到達 ω 天時就會展開。ω 這個符號對應於可數無窮大。在這一天,所有以前不存在的實數,即所有無理數值和所有非二進有理分數,都會一下子被創造出來。
例如,√2 來自以下表示:√2 = {1 5/411/8 ... : ... 23/163/2}。其他無理數值(如 π)也以這種方式獲得;該數字由兩個二進有理數序列包圍。
實際上,該過程類似於已建立的戴德金分割方法,該方法用於從有理數構造實數。在該方法中,形成兩組有理數,其中一組包含小於另一組的數字(就像康威的第一條規則一樣)。然後,這兩組之間的“交集”定義了一個實數。
但在康威的奇特構造中,ω 天誕生了新的數字。突然之間,無限值也出現了——即數字 ω。為此,你必須將所有自然數插入左手集,並將右手集留空:ω = {1 2 3 ... : }。這對應於大於所有自然數的數字。
還有更不尋常的東西。如果你在左手集中輸入 0,並在右手集中輸入所有二進有理分數,你將得到一個無窮小數 ε = {0 : ...1/81/41/2 1}。這個 epsilon 代表無窮大的倒數:ε 非常小,以至於沒有實數可以表示它。事實上,ε 對應於 ω 的倒數:ε = 1/ω。無窮小數 ε 不僅在 ω 天單獨出現,而且還與所有整數和二進有理數組合出現: 1/2 + ε = {1/2 : ... 1/81/41/2 1}。
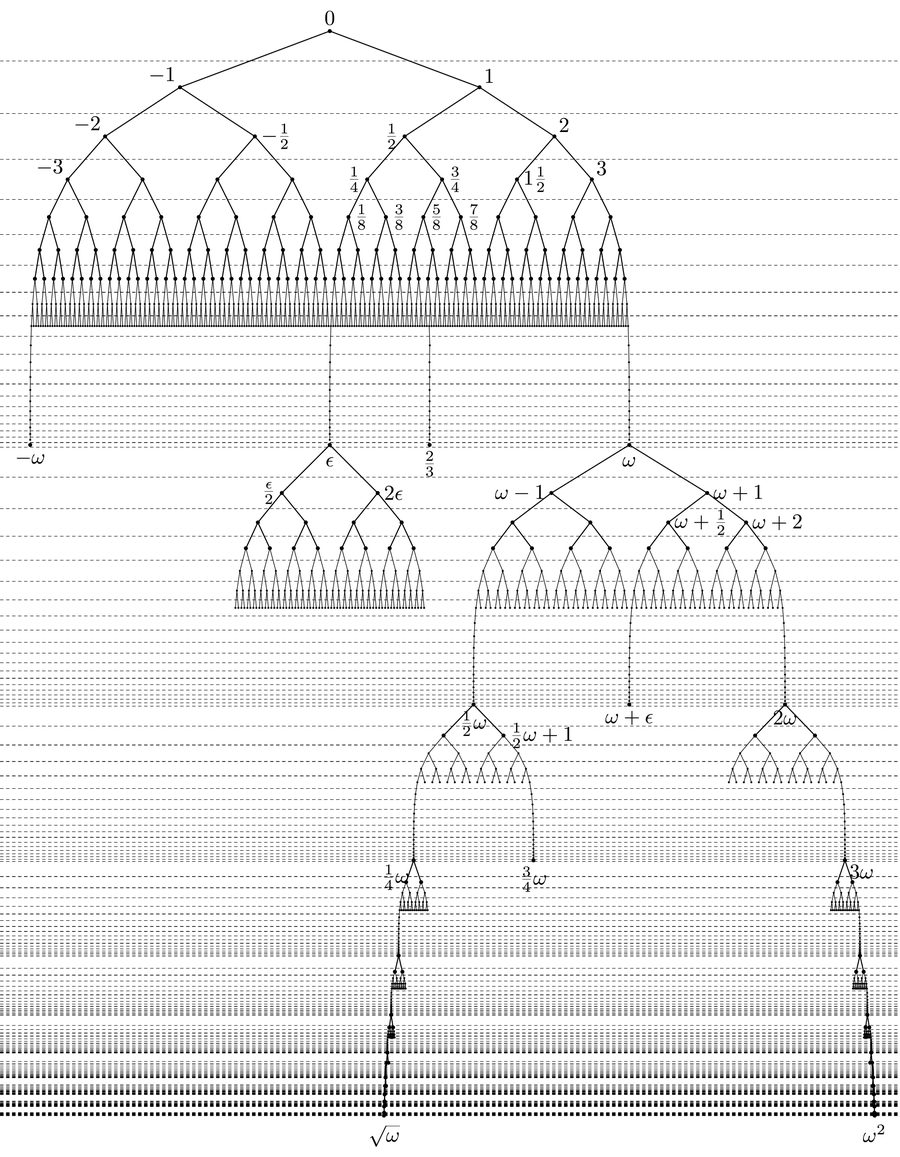
經過無限多天後,從分數到無理數,再到無窮大和無窮小,各種各樣的數字都被創造出來了。 來源:Lukáš Lánský/Wikimedia Commons(CC BY-SA 3.0)
在 ω + 1 天,出現了更多的超現實數,例如數字 ω + 1 和 ω – 1,兩個新的無窮大。此外,任何實數現在都可以與 ε 組合,例如:π + ε = {π : ...1/81/41/2 1}。此外,還建立了數字 ε/2,這是一個比無窮小數小一半的值。
數量的概念崩潰了
在隨後的每一天,都會出現新的超現實數:新的無窮大和無窮小,以及出現在所有先前生成的數字之間的新值。數字的多樣性一點一點地繼續增長。事實上,創造瞭如此多的物件,以至於超現實數不再能被定義為一個集合。相反,它們形成一個“類”。因此,它們遠遠超過所有其他型別的數字:自然數、有理數和實數。
為了理解這一點,回想一下超現實數的定義,即兩個集合 ML 和 MR,其中 ML始終是較小的那個。假設所有超現實數的總體是一個集合 S。那麼你可以將一個新數字 x 定義為 x = {S : }。這將使 x 成為一個超過 S 所有值的數字——所以你將定義一個不包含在 S 中的超現實數。
這是一個矛盾,因為根據定義,S 包含所有超現實數。為了避免這種悖論(如果你想確定所有無窮大的數量,也會出現這種悖論),數學家們引入了類的概念。因為 S 是一個類,所以它不能用於構造超現實數。
超現實數還隱藏著更多的驚喜。儘管超現實數的數量明顯多於實數,但它們並沒有形成連續統。由超現實陣列成的數軸充滿了漏洞——不像實數軸那樣沒有間隙。這些空間的原因是,總是有更小的無窮小量擠在先前生成的超現實數之間。
例如,開集 [0,1) 包括所有小於 1 的值。因此,數字 1 是一個“上限”。然而,超現實數缺少這樣的概念。那是因為你可以在集合 [0,1) 和 1 之間找到一個超現實數,例如 1 – ε。這個數字既不屬於 [0,1) 也不屬於 1。

與實數軸不同,超現實數軸包含較小的無窮小量可以容納的間隙。 來源:Manon Bischoff/Spektrum der Wissenschaft,由 Amanda Montañez 重新設計
這一觀察具有深遠的意義。這意味著諸如 1/n 之類的數字序列,如果 n 趨於無窮大,則不具有極限值 0。相反,該序列不會收斂。它將永遠持續執行,同時它將取越來越小的值 ε, ε/2, ..., ε/100, 等等。在超現實數的宇宙中,0.9999... 永遠不可能等於 1——不像實數那樣。
由於缺少這樣的極限,我們在學校以導數和積分形式學習的常用分析形式也崩潰了。所有基本概念都基於極限值形成和連續數空間。然而,專家們已經成功地開發出所謂的“非標準分析”,它可以與超現實數一起使用。
即使這一切看起來非常抽象和陌生,克努特也確信,超現實數與其他任何數字一樣,都適合描述我們的世界。如果“一百年來每個人都在學校裡學到這個,[他們就會]認為這就是數字的樣子,”他告訴 Numberphile。“我們沒有理由認為宇宙會遵守實數的定律。”事實上,物理學家已經嘗試將超現實數納入他們的理論。然而,所涉及的工作通常非常繁重,到目前為止,收益甚微。
在數學中,超現實數形成了一個有趣的結構:一個龐大的數字系統,可用於描述無窮大和無窮小。康威實際上是在研究圍棋的策略時提出了這種驚人的構造。超現實數已在博弈論中證明了自身的價值,但僅限於其有限的變體,即整數和二進有理數的並集。正如康威在2016 年的一次講座中所反思的那樣,他以這種方式揭示了以前未知的超現實數宇宙的無限廣闊是他“數學生活中最大的驚喜。”
本文最初發表於Spektrum der Wissenschaft,並經許可轉載。
