圓周率 (π) 出現在最不可能的地方。當然,它可以在圓中找到,也可以在擺、彈簧和河流彎道中找到。這個日常數字與先驗的奧秘有關。它啟發了莎士比亞式的思想謎題、烘焙挑戰和甚至是一首原創歌曲。圓周率不斷帶來驚喜——最近一次是在 2024 年 1 月,當時印度科學研究所的物理學家阿爾納布·普里亞·薩哈和阿寧達·辛哈提出了一個全新的公式來計算它,他們後來在《物理評論快報》上發表了這個公式。
薩哈和辛哈不是數學家。他們甚至沒有尋找新的圓周率方程。相反,這兩位弦理論學家正在研究基本力的統一理論,該理論可以調和電磁力、引力以及強核力和弱核力。在弦理論中,宇宙的基本組成部分不是粒子(如電子或光子),而是像吉他的弦一樣振動的細小絲線,這樣做會引起所有可見現象。在他們的工作中,薩哈和辛哈研究了這些弦如何相互作用——並意外地發現了與重要數學量相關的新公式。
幾千年來,人類一直試圖確定圓周率的精確值。考慮到計算圓的周長或面積的實用性,這並不奇怪,而圓周率使之成為可能。甚至古代學者也開發了幾何方法來計算這個值。一個著名的例子是阿基米德,他藉助多邊形估算了圓周率:透過在一個圓內和一個圓外繪製一個n邊形並計算每個多邊形的周長,他能夠縮小圓周率的值。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的有影響力的故事的未來。
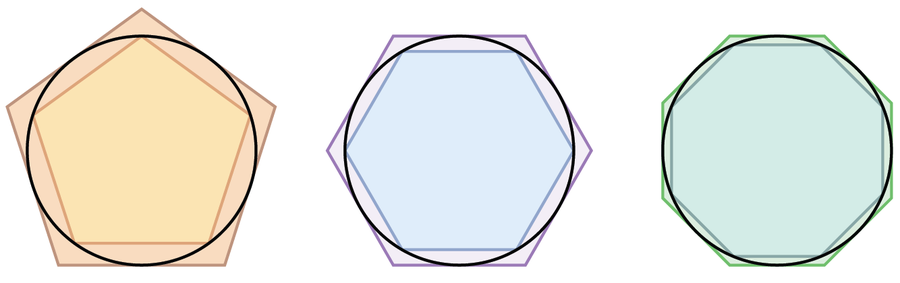
一種常見的幾何方法是繪製一個圓的內接和外切多邊形,然後比較兩個周長,以此來確定圓周率。
Fredrik/Leszek Krupinski/維基共享資源
教師經常在學校裡介紹這種方法。但即使您不記得了,您也可能可以想象到這個過程非常複雜。阿基米德甚至比較了具有 96 個頂點的多邊形的周長,以證明圓周率介於 3.1408 和 3.1429 之間。因此,這種方法實際上並不適用於精確計算圓周率。
確定圓周率的無窮級數
在 15 世紀,專家們發現了無窮級數,作為表達圓周率的新方法。透過將它們的數字逐個相加,可以獲得圓周率的值。您檢視的被加數越多,結果就越準確。
例如,印度學者馬達瓦(生活於 1350 年至 1425 年)發現圓周率等於4 乘以一個級數,該級數以 1 開頭,然後交替減去或加上分數,其中 1 位於連續更高的奇數之上(因此為 1/3、1/5 等)。一種表達方式是

這個公式使得以非常簡單的方式儘可能精確地確定圓周率成為可能。您不必成為數學大師也能解出這個方程。但您確實需要耐心。獲得準確的結果需要很長時間。即使您評估 100 個被加數,您仍然會離目標很遠。
正如薩哈和辛哈在 600 多年後發現的那樣,馬達瓦的公式只是一個更通用的圓周率計算公式的特例。在他們的工作中,弦理論學家發現了以下公式
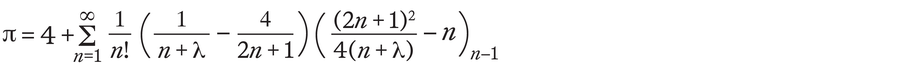
這個公式產生一個無限長的和。引人注目的是它取決於因子 λ,這是一個可自由選擇的引數。無論 λ 取何值,該公式始終會得出圓周率。並且由於有無限多的數字可以對應於 λ,薩哈和辛哈發現了無限多個圓周率公式。
如果 λ 無限大,則該方程對應於馬達瓦公式。也就是說,因為 λ 始終只出現在分母的分數中,所以 λ = ∞ 的相應分數變為零(因為分母大的分數非常小)。對於 λ = ∞,薩哈和辛哈的方程因此採用以下形式

方程的第一部分已經類似於馬達瓦公式:您對分母為奇數的分數求和。然而,和的最後一部分 (–n)n – 1不太熟悉。下標n – 1 是所謂的波赫哈默符號。一般來說,表示式 (a)n 對應於乘積a x(a + 1) x (a + 2) x ... x (a + n – 1)。例如,(5)3 = 5 x 6 x 7 = 210。因此,上述公式中的波赫哈默符號得出:(–n)n – 1 = (–n) x (–n + 1) x (–n + 2) x ... x (–n + n – 3) x (–n + n – 2)。
簡化為馬達瓦公式的幾個步驟
所有這些元素乍一看都很複雜,但它們可以很快簡化。首先,從每個因子中減去 -1。因此,如果n是奇數,則巨大乘積前面的符號為 -1,如果n是偶數,則為 +1,因此您得到 (–n)n – 1 = (–1)n x n x (n – 1) x (n – 2) x ... x (n – n + 3) x (n – n + 2)。最後一個因子可以進一步簡化:(–n)n – 1 = (–1)n x n x (n – 1) x (n – 2) x ... x 3 x 2 x 1。
這個拉長的表示式實際上是 (–n)n – 1 = (–1)nx n!,結果如下。*

這對應於馬達瓦公式。因此,薩哈和辛哈發現的方程也包含馬達瓦發現的級數。
正如兩位弦理論學家報告的那樣,對於較小的 λ 值,圓周率的計算速度要快得多。雖然馬達瓦的結果需要 100 項才能達到圓周率的 0.01 範圍內,但薩哈和辛哈的 λ = 3 公式僅需要前四個被加數。“雖然 [馬達瓦的] 級數需要 50 億項才能收斂到小數點後 10 位,但 λ 在 10 [到] 100 之間的新表示形式需要 30 項,”作者在他們的論文中寫道。 薩哈和辛哈沒有找到計算圓周率的最有效方法。幾十年來,人們已經知道其他一些級數可以更快地提供令人驚訝的精確值。在這種情況下真正令人驚訝的是,物理學家在他們的論文旨在描述弦的相互作用時,提出了一個新的圓周率公式。他們開發了一種方法來指示兩個閉弦相互作用的機率——許多弦理論學家幾十年來一直在尋求但未成功的方法。
當薩哈和辛哈仔細研究由此產生的方程時,他們意識到他們可以用這種方式表達圓周率,以及 zeta 函式,zeta 函式是黎曼猜想的核心,黎曼猜想是數學中最偉大的未解之謎之一。鑑於弦理論學家的興趣,他們關於圓周率和 zeta 函式的公式僅裝飾了他們論文的最後一段。“當然,我們的動機不是找到圓周率的公式,”辛哈在 Numberphile 的 YouTube 影片中說。“圓周率只是副產品。”
本文最初發表在《光譜》雜誌上,經許可轉載。
*編者注(2024 年 9 月 4 日):這句話在釋出後進行了編輯,以更正最初遺漏階乘符號的方程。
