第三方總統候選人經常被指責透過“竊取”主要政黨的選票來破壞選舉。但是,藉助社會選擇理論的數學,選舉可以擁抱像拉爾夫·納德這樣的世界。
以2000年美國總統大選戈爾對布什的歷史性膠著局面為例,當時美國人焦急地等待法律戰的解決和重新計票,而重新計票在一個月內都不會揭曉獲勝者。《洋蔥報》當時釋出了標題為“重新計票顯示納德擊敗”的新聞。當然,拉爾夫·納德從來都不是有力的競爭者。這導致許多人認為,綠黨候選人,像其他第三方政治家一樣,從兩大主要政黨之一那裡吸引了足夠的選票,從而使天平向他們傾斜(在本例中是民主黨人,他們僅以537票的差距輸掉了選舉)。
排序複選投票是一種替代選舉制度,社會選擇理論家認為,它可以減輕“劇透效應”,同時讓選民在投票時有更多的發言權。排序複選投票具有一些明顯的優勢。然而,關於如何最好地實施它的數學討論卻出人意料地微妙。 而經濟學中的一個古老定理表明,所有使用排序複選投票的嘗試都容易受到違反直覺的結果的影響。
關於支援科學新聞業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞業: 訂閱。透過購買訂閱,您正在幫助確保未來能夠繼續講述關於塑造我們當今世界的發現和想法的具有影響力的故事。
排序複選投票允許人們按偏好順序對候選人進行排序,而不是隻投票給一位候選人。這樣,如果有人想支援納德,但又不想從戈爾那裡奪走選票,他們可以在投票站將戈爾排在第二位。當納德沒有獲得足夠的選票時,戈爾的第二名排名仍然會在選舉中使他受益。支持者還認為,排序複選投票會抑制惡意的誹謗競選策略。這是因為,與典型的選舉不同,排序複選投票中的候選人需要吸引所有選民,即使是那些不會在選票上給他們第一名的人。目前,緬因州和阿拉斯加州已對所有州和聯邦選舉實行排序複選投票,包括總統初選,在總統初選中,多位候選人更有可能吸引相同的選民。
一旦選民對候選人進行排序,如何彙總這些資訊以揭示唯一的獲勝者?答案並不像看起來那麼簡單,並且已經提出了許多方案。讓我們探討三種計票方法:簡單多數制、即時決勝制和“孔多塞方法”,每種方法都會導致意想不到的行為。
與即時決勝制和孔多塞方法不同,簡單多數制實際上並不是一種排序複選投票方案。事實上,它是美國最常見的投票方法:誰獲得的第一選擇票最多,誰就贏得選舉。簡單多數制可能會帶來不利的結果。除了第三方選舉攪局者的問題外,想象一下,如果候選人A獲得34%的選票,而候選人B和C各獲得33%的選票。即使候選人A是其他所有選民的最後選擇,他也會以簡單多數獲勝。因此,66%的人口會選擇他們最後選擇的總統。簡單多數制浪費選票,並忽略了選民偏好的全部範圍。
一種更好的方法(也是美國實施排序複選投票以及奧斯卡金像獎最佳影片評選中使用的方法)稱為即時決勝制。如果沒有候選人獲得超過一半的第一選擇票,那麼第一選擇票最少的候選人將被排除在考慮範圍之外,他們的選票將根據選民的下一個選擇重新分配(例如,如果您的三位候選人排名是 1) B, 2) C, 3) A,並且候選人 C 因第一選擇票最少而被移除,那麼 A 將在您的選票中被提升以填補 C 的空缺:1) B, 2) A)。刪除第一選擇票最少的候選人的過程重複進行,直到一位候選人獲得多數票。 雖然即時決勝制比簡單多數制浪費的選票更少,但它也有自身的缺點。可能會出現奇怪的情況,即您最喜歡的候選人如果獲得更多的第一選擇票,反而更有可能輸掉選舉。
下圖(基於 electionscience.org 的一個例子)描述了這種情況。在一個假設的即時決勝選舉(稱為選舉 1)中,候選人 A 獲勝。儘管 A 和 B 擁有相同數量的第一選擇票,但兩者都沒有贏得選舉所需的多數票(17 票中的 9 票)。因此,第一選擇票最少的 C 被排除在競爭之外,並且調整選票以填補 C 的空缺,從而為候選人 A 贏得多數票。
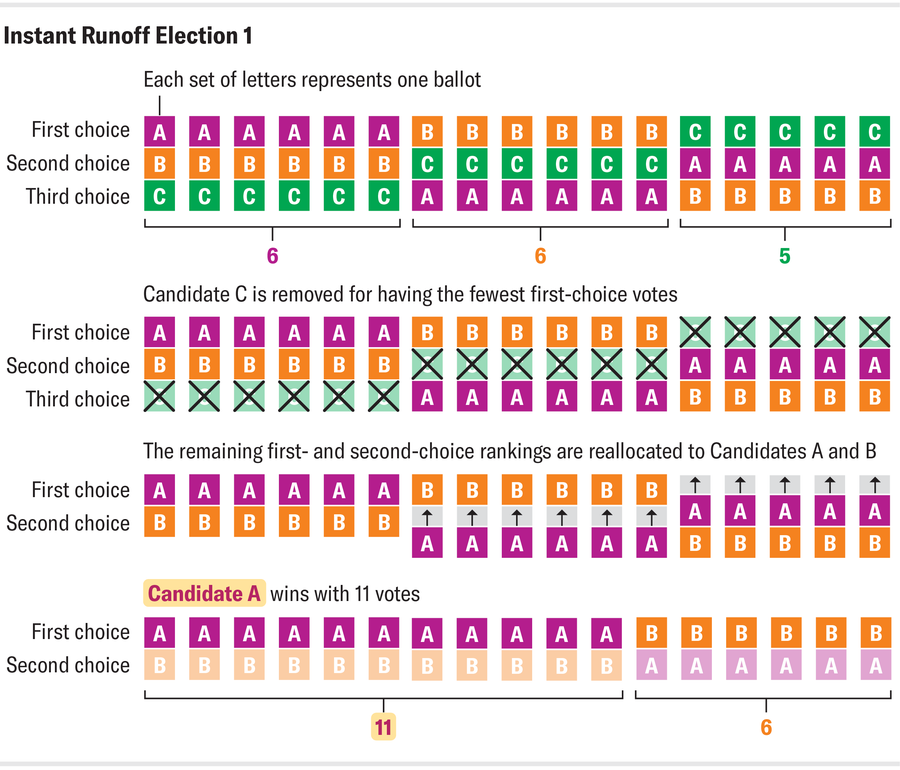
來源:Amanda Montañez;來源:https://electionscience.org/library/monotonicity/
現在想象一下另一種情況,稱為選舉 2,其中每個人都以與選舉 1 相同的方式投票,除了兩個人將 A 從他們的第三選擇升級為第一選擇。令人驚訝的是,即使 A 贏得了選舉 1,並且現在比以前擁有更多的第一選擇票,C 也成為了新的獲勝者。這是因為升級 A 會導致 B 降級,因此 B 現在是第一選擇票最少的候選人。當 B 被移除時,A 在與 C 的一對一較量中不如他們在選舉 1 中與 B 的較量那樣順利。
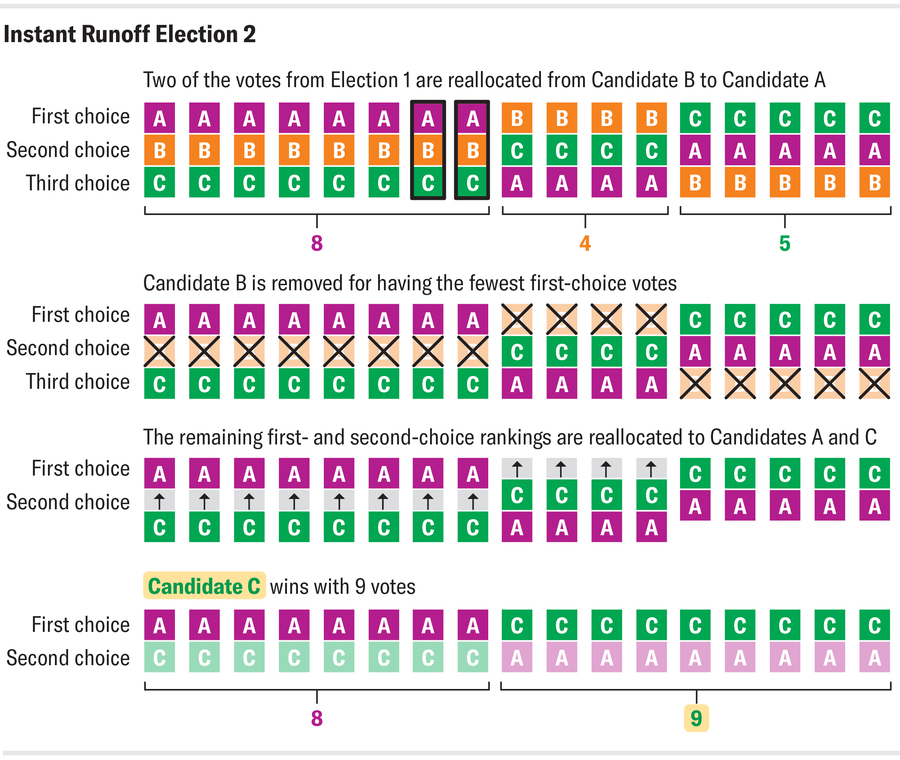
來源:Amanda Montañez;來源:https://electionscience.org/library/monotonicity/
這種違反直覺的現象發生在佛蒙特州伯靈頓市 2009 年的市長選舉中,進步黨成員鮑勃·基斯在即時決勝選舉中擊敗了共和黨和民主黨提名人。令人驚訝的是,如果更多的選民將基斯放在他們的排名第一位,他就會輸掉選舉。
孔多塞方法,以 18 世紀法國數學家和政治哲學家孔多塞侯爵的名字命名,選出一位在與任何其他候選人的一對一選舉中都會獲勝的候選人。例如,假設在 2000 年沒有任何第三方候選人的選舉中,阿爾·戈爾本可以擊敗喬治·W·布什。戈爾當然也會在與任何一位第三方候選人的一對一競爭中獲勝。戈爾贏得任何假設的一對一選舉都將使他成為所謂的孔多塞候選人。看起來很明顯,這樣的候選人應該是勝利者,因為民眾更喜歡他們而不是所有的對手。但是,在選舉孔多塞候選人時,這裡有一個重要的障礙:他們並非總是存在。選民的偏好可能是迴圈的,例如民眾更喜歡 A 而不是 B,更喜歡 B 而不是 C,但也更喜歡 C 而不是 A。這種違反傳遞性的現象被稱為孔多塞悖論(並且讓人想起非傳遞骰子,我最近寫過關於它的文章)。
已經提出了幾種其他將排名選票合併為獲勝者的方案。它們各有優缺點,更令人不安的是,選舉結果可能完全取決於使用哪種制度。
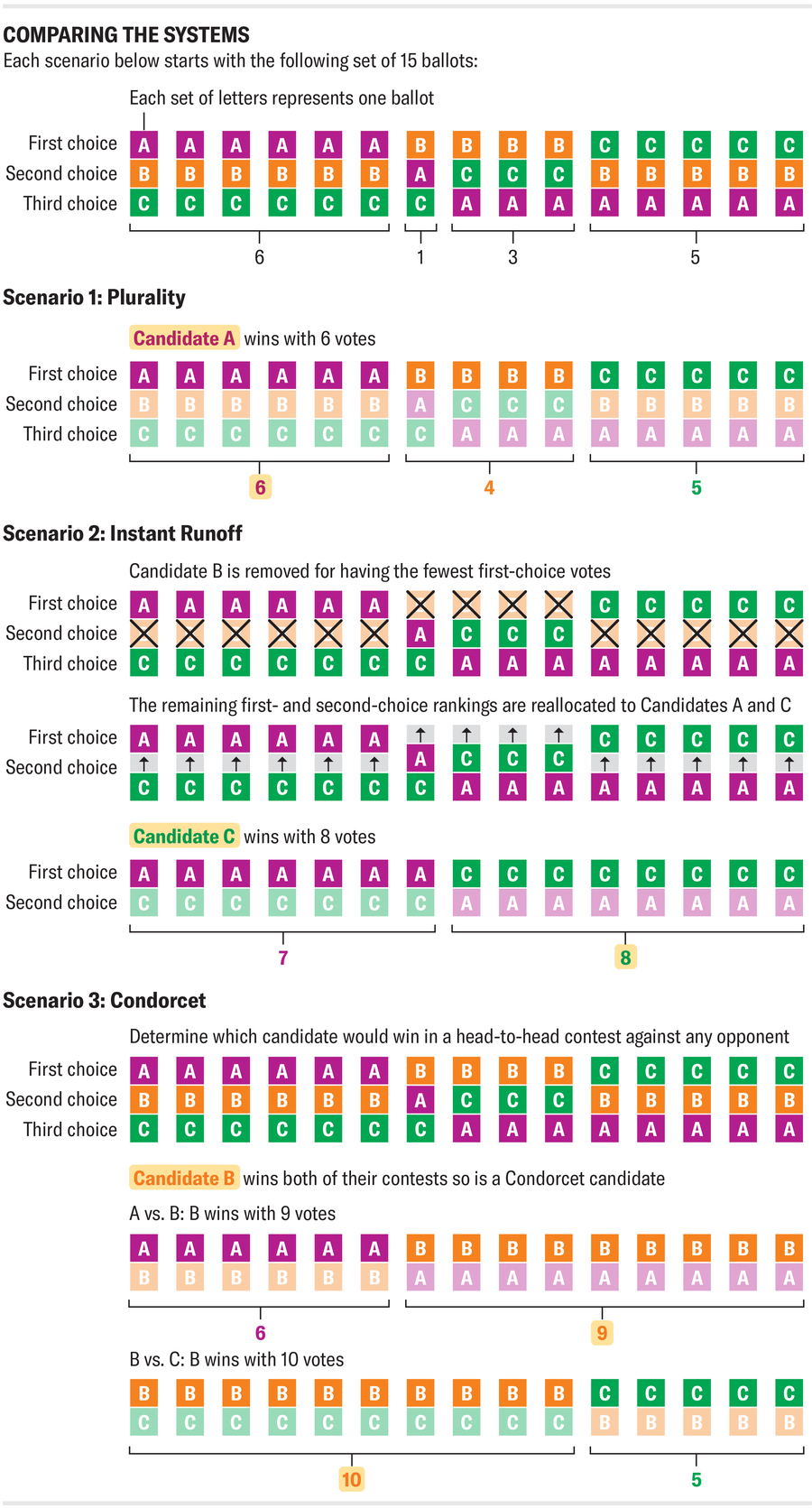
來源:Amanda Montañez
該圖顯示了一個簡單的選舉,在我們討論的三種制度下產生了不同的結果。這種比較引出了一個充滿希望的問題:是否存在完美的排序複選投票制度?也許我們只是尚未發現理想的設計,它可以在最大限度地代表公眾利益的同時,避免現有提案的缺陷。諾貝爾經濟學獎獲得者肯尼斯·阿羅研究了這個問題,並提出了任何合理的聚合器(或將選民排名轉換為一個社會排名的方法)的最低要求:
一致性:如果人口中的每個人都將候選人 A 排在候選人 B 之上,那麼聚合器應將候選人 A 排在候選人 B 之上。
無關選項的獨立性:假設聚合器將候選人 A 排在候選人 B 之上。如果選民要更改他們的一些排名,但每個人都保持他們對 A 與 B 的相對順序不變,那麼 A 在新的聚合排名中應保持在 B 之上。A 和 B 的社會排序應僅取決於 A 和 B 的個人排序,而不取決於其他候選人的排序。
這個常識性的清單設定了很低的門檻。但是阿羅證明了一個驚人的事實,這個事實後來被稱為阿羅不可能定理:只有一種型別的聚合器可以同時滿足這兩個條件,那就是獨裁統治。阿羅所說的獨裁統治是指一個荒謬的聚合器,它總是簡單地模仿同一個選民的排名。沒有任何排序複選投票方案,無論它多麼聰明或複雜,都可以在滿足一致性和無關選項獨立性的同時,除非它是獨裁統治。該定理表明,沒有完美的排序複選投票方案,我們總是不得不應對不良或違反直覺的結果。
這個證明並不意味著我們應該放棄排序複選投票。與簡單多數制投票相比,它在捕捉選民意願方面仍然做得更好。這僅僅意味著我們需要挑選並選擇我們希望聚合器具有哪些屬性,並承認我們不能擁有一切。該定理並沒有說每次選舉都會有缺陷,而是說沒有哪種排序複選選舉制度是不會出現缺陷的。阿羅曾評價他自己的結果:“大多數系統不會一直都很糟糕。我所證明的只是所有系統有時都可能很糟糕。”
我們中的理想主義者不應失去希望,因為排序複選投票並不是改進型選舉制度的唯一選擇。僅僅對候選人進行排名會丟失大量關於選民偏好的資訊。例如,這是我對想吃的食物從最想要到最不想要的排名:香草冰淇淋 > 巧克力冰淇淋 > 我自己的運動鞋。排名沒有傳達出我對香草和巧克力冰淇淋的喜愛程度有多接近,也沒有傳達出我對我的耐克鞋有多厭惡。為了正確表達我的願望,我應該給候選食物打分,以傳達我不僅更喜歡哪些食物,而且喜歡多少。這被稱為基數投票或範圍投票,雖然它不是萬能藥,並且有其自身的缺點,但它規避了阿羅不可能定理的限制,該定理僅適用於排序複選投票。
我們都熟悉基數投票。在奧林匹克體操比賽中,評委透過給參賽者打出數字分數來決定獲勝者,最終總分最高的人獲勝。每當您在網上按消費者星級評分對產品進行排序時,您都會看到基數選舉的獲勝者。古代斯巴達人透過聚集在一個議會上,輪流為每位候選人吶喊來選舉領導人。誰獲得的吶喊聲最大,誰就贏得了選舉。雖然這在現代人聽起來很粗糙,但這實際上是基數投票的早期形式。人們可以投票給多位候選人,並透過選擇向人群的咆哮聲貢獻多少音量來“評分”。考慮到基數投票儘管比我們討論過的任何其他制度都賦予了人民更多的發言權,但從未在現代選舉中使用過,這令人印象深刻。也許我們不應該感到驚訝:畢竟,古希臘人確實發明了民主。
